西尔维斯特方程(Sylvester equation)以英国数学家James Joseph Sylvester的名字命名,是控制理论中著名的矩阵方程[1]。求解西尔维斯特方程一般有串行处理和并行处理两种方法,但是在很多工程领域的研究中,只有并行处理才能解决复杂的随时间变化的问题,比如图像处理、机械臂[2]、轨迹规划、现场可编程门阵列[3](field-programmable gate array,FPGA)、神经网络等,所以在线实时求解西尔维斯特方程对许多研究都非常重要。
随着科技的发展,与传统的方法相比,神经动力学具有更出色的性能,而且满足了在工程中能处理大量数据和实时计算的需求,因此研究者提出了多种基于梯度的递归神经网络以求解实值领域的随时间变化的西尔维斯特方程[4]。递归神经网络(recurrent neural network,RNN)[5-6]只保留了定义的误差函数的范数,忽视了一些随时间变化的误差信息,所以表现比较一般。基于此,Zhang等[7-9]提出归零神经网络(zeroing neural network,ZNN),通过对时间的一阶导数的充分利用,能有效消除随时间变化的误差信息的残差。随着对递归神经网络的研究越来越深入,在信号处理[10]领域,涌现了越来越多需要运用复数解决的问题,比如频域在线识别或输入信号包含振幅和相位信息的情况。因此,人们开始研究实时解决复数矩阵问题的神经动力学方法[11],从而提出了复数归零神经网络(complex-valued zeroing neural network,CVZNN)模型[12]和各种激活函数[13]。高畅等[14]提出了新型有限时间归零神经网络(new finite-time zeroing neural network,NFTZNN)模型,将一种新型激活函数引入NFTZNN模型,从而提高收敛性能。
模糊控制将多学科,如概率论、运动学、物理学等,通过模糊集合和模糊逻辑推理转化成数字或数字函数,再用计算机实现控制[15]。模糊逻辑系统以模糊控制为核心,应用于多个领域,如航天器、机器人[16]、汽车等。模糊控制易于被操作人员接受,便于用计算机软件实现,鲁棒性和适应性好,而神经网络具有较高的计算效率,将模糊控制引入神经网络[17],能代替人们在自动化和智能系统等领域中处理一些高难度的工作。
针对CVZNN模型求解复值矩阵问题收敛速度慢且计算精度低的问题,本研究提出加入模糊逻辑系统来求解复数时变矩阵,称之为模糊归零神经网络(fuzzy logic system for zeroing neural network,FLSVZNN)。与之前常用的收敛参数不同,输入误差函数,由模糊逻辑系统(fuzzy logic system,FLS)生成一个模糊的功率参数,并将其嵌入到模型中,从而调整收敛速度,进行理论分析并与CVZNN模型进行比较。此外,还进行了两种实例的模拟试验,展示了两种FLSVZNN模型在几种常用激活函数下的优势。
1 提出问题和建立模型1.1 问题描述西尔维斯特方程是控制理论中的矩阵方程,形式如下:
U(t)X(t)+X(t)V(t)-W(t)=0。(1)
式(1)中:U(t)、V(t)、W(t)为n阶时变复数矩阵; X(t)为需求解的复数矩阵; t为时间。
为了使上述的西尔维斯特方程成立,矩阵的行数和列数需满足一定的条件,U(t)和V(t)为n阶和m阶方阵,W(t)和X(t)为n行m列的矩阵。式(1)中,m=n,这说明X(t)有解且可以被求解。为了使X(t)有唯一解,U(t)和-V(t)还需满足没有共同的特征值。
为了求解式(1),根据实域中ZNN模型的设计方法,建立CVZNN模型来求解复数时变问题。
1)构造复数的误差函数
E(t)=U(t)X(t)+X(t)V(t)-W(t)。(2)
2)定义E(t)的演化过程如下:

式(3)中:γ1>0为可以调节的正值参数; Φ(·)为复数中的激活函数。
3)将式(2)代入式(3),可得随时间变化的西尔维斯特方程:

然后在标准ZNN模型式(4)的基础上,将实数域扩展到复数域。
1.1.1 CVZNN-Ⅰ模型CVZNN-Ⅰ模型的处理方法是同时激活复数输入的实部和虚部。具体描述如下:
Φ1(E(t))=Ω(Ere(t))+iΩ(Eim(t))。(5)
式(5)中:Ω(·)为实数的激活函数; Ere(t)和Eim(t)分别为E(t)的实部和虚部。
根据式(4)和式(5)可得如下CVZNN-Ⅰ模型:
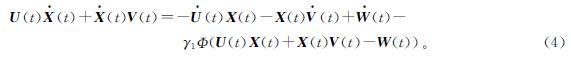
式(6)中:Ere(t)和Eim(t)由A(t)和B(t)来表示U(t)X(t)+X(t)V(t)-W(t)的实部和虚部。
1.1.2 CVZNN-Ⅱ模型CVZNN-Ⅱ模型的处理方法是激活复数输入的模,定义如下:
Φ2(E(t))=Ω(C(t))·exp(iD(t))。(7)
式(7)中:C(t)和D(t)分别为复数误差函数E(t)的模和辐角。
由式(4)和式(7)可得:
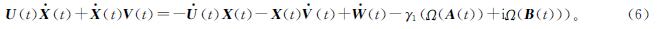
模糊逻辑是一种使用隶属度来代替传统的布尔真值的逻辑系统,与经典的二值逻辑不同,它并不使用截然不同的0和1来表达,而是使用隶属度来表达,以更好地反映现实生活中的不确定性和模糊性。这使得模糊逻辑成为一个有力的工具,可以处理那些无法被明确定义的情况,也可以在计算机中更有效地处理不确定的信息。
在传统的控制领域中,通常更精确的信息和更详细的系统建模可以提高控制系统的性能。复杂的系统由于变量太多往往很难控制,而模糊控制鲁棒性强、抗干扰性能力好,在解决这类问题上表现出色。模糊逻辑系统是一种基于模糊逻辑的控制系统,它能在输入变量模糊的情况下,通过一系列模糊逻辑运算,输出模糊变量的结果。模糊系统的输入和输出通常用模糊集合来描述,模糊推理引擎中的规则和推理是模糊控制的核心。
本研究引入一个由模糊逻辑系统生成的模糊参数v代替之前的收敛参数,从而加速FLSVZNN模型的收敛过程,考虑到输入的e与期望的模糊参数v有关,制定了以下模糊逻辑方案。
第一个步骤是模糊化。隶属函数是用于表征模糊集合的数学工具,通常用来描述模糊集合的形状,将精确的输入值映射为0到1之间的模糊值。模糊化就是利用隶属函数,将输入e映射到模糊输入子集E,设定输出v和模糊输出子集V。隶属函数可以采用不同的形状,包括高斯形、三角形、梯形、S形曲线等,本研究中模糊控制系统的输入e和输出v的隶属函数分别采用如下高斯函数和三角函数。
1)高斯函数
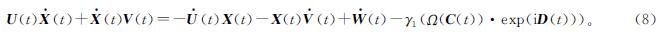
式(9)中:c为函数中心的位置; σ为函数曲线的宽度。
2)三角函数

式(10)中:a≤b≤c。
第二个步骤是制定模糊推理引擎。模糊推理引擎是模糊控制的核心,负责执行推理过程,将模糊输入和模糊规则转化为模糊输出,并最终将其映射为实际的操作或决策,使模糊控制能在各种领域中灵活应用。在上一步模糊化操作完成后,输入e转换成了模糊输出子集E,接下来需要明确定义一组模糊规则,这些规则描述了模糊输入子集E和模糊输出子集V之间的关系,这些关系遵循如下规则:
R1:若E为ZO,则V为ZO;
R2:若E为PS,则V为PS;
R3:若E为PB,则V为PB。
其中ZO(零)、PS(正小)和PB(正大)是模糊子集。输出参数v会随着输入的数值误差e变化,e变大v也会变大,e变小则v也会随之变小,以此来实现复值模糊归零神经网络的可控收敛。基于3个模糊规则,可得:
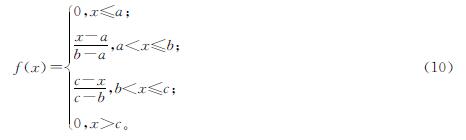
式(11)中: 为模糊变换符号; i=1,2,3,表示E通过相关规则转换成V。具体的变换内容如下:
为模糊变换符号; i=1,2,3,表示E通过相关规则转换成V。具体的变换内容如下:

式(12)中: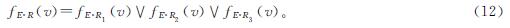 ,用∧和∨表示最大运算和最小运算。
,用∧和∨表示最大运算和最小运算。
第三个步骤是清晰化。为了获得最终的输出常量,需去模糊化操作,有面积中心法、面积平分法及平均最大隶属度法等。本研究采用了平均最大隶属度法:
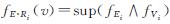
引入模糊逻辑系统生成的模糊参数v后,设计新的随时间变化的FLSVZNN模型如下:

式(14)中:r2>1。
然后将实值域推广到复值域,以求解复数西尔维斯特方程。通过以上方法,可以得到求解复数西尔维斯特方程的相应的两个FLSVZNN模型。
由式(5)和式(14),可得如下FLSVZNN-Ⅰ模型:

根据式(7)和式(14),可得如下FLSVZNN-Ⅱ模型:
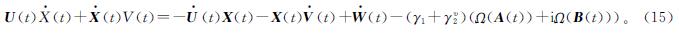
越来越多的激活函数被用来改善神经网络的收敛性能。
1)线性函数
Ω(x)=x。(17)
2)功率函数
Ω(x)=xk,k为奇数,k≥3。(18)
3)双相符号函数
Ω(x)=(1+e-m)/(1-e-m)(1-e-mx)/(1+e-mx),m>2。(19)
4)符号双幂(sign-bi-power,SBP)函数
Ω(x)=1/2|x|msign(x)+1/2|x|1/msign(x)。(20)
式(20)中:m∈(0,1),x∈R。
5)改进的SBP函数
Ω(x)=1/2|x|msign(x)+1/2x+1/2|x|1/msign(x)。(21)
与SBP函数相比,改进的SBP函数有一个额外的线性项。因此,在FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型中,使用改进的SBP函数来激活比使用SBP函数来激活效果更好。
2 收敛性能分析定理1 给定光滑的时变复矩阵U(t)、V(t)、W(t),当使用激活函数Ω(x)=x时,FLSVZNN-Ⅰ模型的矩阵X(t)能从随机原始状态X(0)收敛到时变复数西尔维斯特方程的理论解X*(t)。
证明:根据式(3)、式(5)和式(15)可知A(t)和B(t)等价于以下两个方程:
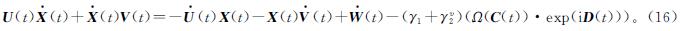
式(23)中:aij(t)为A(t)中第i行j列的值。定义李亚普诺夫函数L=1/2a2ij(t),可得L ·=aij(t)a ·ij(t)=-(γ1+γv2)aij(t)Ω(aij(t))。由于激活函数Ω(x)=x是单调递增的奇函数,故满足Ω(aij(t))=-Ω(-aij(t))。因为γ1>0,γ2>1,v>0,所以γ1+γv2>0。当aij(t)≥0时,因为Ω(x)=x,所以Ω(aij(t))≥0,李亚普诺夫函数的导数L ·≤0; 当aij(t)<0时,Ω(aij(t))<0,L ·<0。bij(t)的结果同理可得。
因此,对于误差函数A(t)和B(t)任意i行j列的值,L ·恒小于等于0。那么根据李亚普诺夫定理,这两个动态系统将收敛到它们的平衡点,即A(t)和B(t)都随时间收敛至0,可得误差函数E(t)能最终全局收敛。根据E(t)的定义,FLSVZNN-Ⅰ模型能全局稳定收敛,被求解的矩阵X(t)能从随机原始状态X(0)收敛至理论解X*(t)。
定理2 给定光滑的时变复矩阵U(t)、V(t)、W(t),当使用激活函数Ω(x)=x时,FLSVZNN-Ⅱ模型的矩阵X(t)能从随机原始状态X(0)收敛到时变复数西尔维斯特方程的理论解X*(t)。
从FLSVZNN-Ⅱ模型中可以得到如下非线性动态子函数:
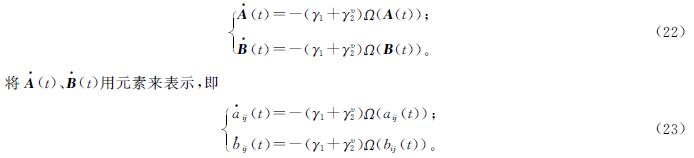
式(24)中:e ·ij(t)、cij(t)、dij(t)分别为矩阵函数E ·(t)、C(t)和D(t)第i行j列的值; Ω(·)中cij(t)和dij(t)分别为复数变量eij(t)的模和辐角。

考虑到Ω(x)=x是一个单调递增的奇函数,γ1>0,γ2>1,v>0,可得γ1+γv2>0。那么当eij(t)≥0时,因为Ω(x)=x,所以Ω(eij(t))≥0,李亚普诺夫函数的导数L ·≤0; 当eij(t)<0时,Ω(eij(t))<0,L ·<0。可知,L ·恒小于等于0。根据李亚普诺夫理论,对于误差函数E(t)任意i行j列的值,都能全局收敛,即误差函数E(t)最终能全局收敛。根据E(t)的定义,FLSVZNN-Ⅱ模型能全局稳定收敛,被求解的矩阵X(t)能从随机原始状态X(0)收敛至理论解X*(t)。
定理3 给定光滑的时变复矩阵U(t)、V(t)、W(t),当使用激活函数Ω(x)=x时,FLSVZNN-Ⅰ模型的收敛速度为γ1+γv2,比CVZNN-Ⅰ模型收敛速度更快。
q(t)记录aij(t)和bij(t)的最大绝对值,当t=0时,可以取得较大的初始值,记为q(0)=max{|aij(0)|,|bij(0)|}。此外,可以得到-|q(t)|≤|aij(t)|≤|q(t)|和-|q(t)|≤|bij(t)|≤|q(t)|。换言之,当q(t)=0时,A(t)和B(t)中的所有元素都可以达到0。则q(t)随时间变化表现为q ·(t)=-(γ1+γv2)Ω(q(t))。
定义了一个李亚普诺夫函数L(t)=|q(t)|2,并求解了L(t)随时间变化的时间导数,因为使用Ω(x)=x,可得L·(t)=-2(γ1+γv2)q(t)2=-2(γ1+γv2)L(t)。由上式可得1/(L(t))dL(t)=-2(γ1+γv2)dt,求解上述等式,可以得到L(t)=L(0)·e-2(γ1+γv2)t,其中L(0)=|q(0)|2,因此q(t)=q(0)·e-(γ1+γv2)t。由于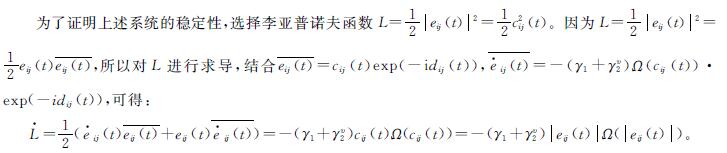 ,可知
,可知 。
。
一般情况下,可以得出具有任意初值的FLSVZNN-Ⅰ模型的收敛速度为γ1+γv2。同理可得,当没有使用由模糊逻辑系统产生的模糊参数v时,使用参数为γ1的CVZNN-Ⅰ模型的收敛速度为γ1。因为γ1>0,γ2>1,v>0,所以γ1+γv2>γ1,故FLSVZNN-Ⅰ模型比CVZNN-Ⅰ模型收敛速度更快。
定理4 给定光滑的时变复矩阵U(t)、V(t)、W(t),当使用激活函数Ω(x)=x时,FLSVZNN-Ⅱ模型的收敛速度为γ1+γv2,比CVZNN-Ⅱ模型收敛速度更快。
计算FLSVZNN-Ⅱ模型收敛速度的方法与FLSVZNN-Ⅰ模型的方法相似。首先,定义李亚普诺夫函数L(t)=|u(t)|2,其中u(t)满足|u(t)|=max|eij(t)|=max|cij(t)|。显然,当u(t)=0时,|u(0)|=max|eij(0)|=max|cij(0)|,E(t)中的所有元素都可以收敛至0。通过计算u(t)的收敛速度,可以预测FLSVZNN-Ⅱ模型的收敛速度。u(t)的动态演化如下:u ·(t)=-(γ1+γv2)Ω(u(t))。
根据计算,可以进一步得到L ·(t)=-2(γ1+γv2)u(t)Ω(u(t))=-2(γ1+γv2)u2(t)。然后,类似于FLSVZNN-Ⅰ模型的证明,可以得出具有任意初值的FLSVZNN-Ⅱ模型的收敛速度为γ1+γv2。同理可得,当没有使用由模糊逻辑系统产生的模糊参数v时,使用参数为γ1的CVZNN-Ⅱ模型的收敛速度为γ1。因为γ1>0,γ2>1,v>0,所以γ1+γv2>γ1,故FLSVZNN-Ⅱ模型比CVZNN-Ⅱ模型收敛速度更快。
3 模拟验证以下给出两个具体的例子,利用激活函数Ω(x)=x,验证FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型的有效性。
例1 考虑了具有以下系数U(t)、V(t)、W(t)和γ1=1、γ2=5的复值时,变西尔维斯特方程
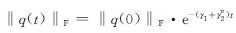
求解可知U(t)的特征值λ1=e5it,λ2=sin(5t)+cos(5t)i; V(t)的特征值λ1=0,λ2=0。U(t)和-V(t)没有共同的特征值,满足X(t)是唯一解。
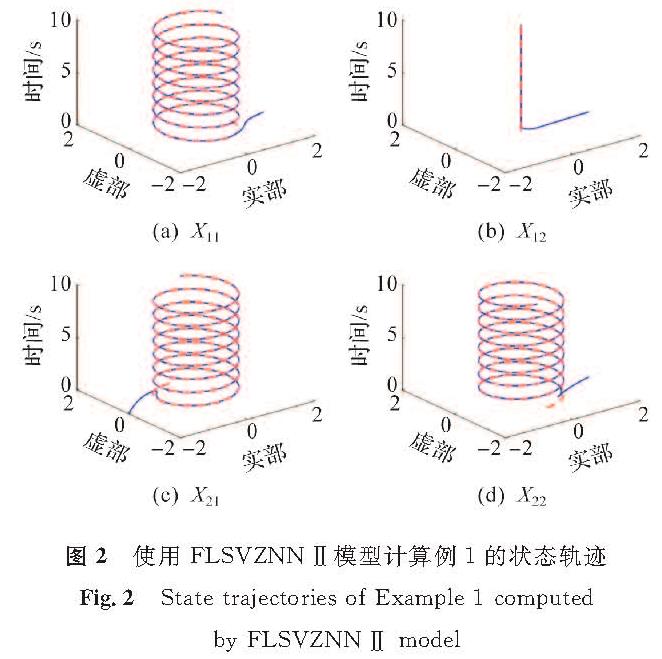
使用FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型计算例1的状态轨迹,分别如图1和图2所示,可知这两种模型在激活函数Ω(x)=x的激活作用下,都可以从一个特定的初始状态X(0)=[2,2; -2,2]开始,使复数矩阵X(t)从用实心蓝线表示的状态解收敛到用红色虚线表示的理论解,有较好的收敛性能。
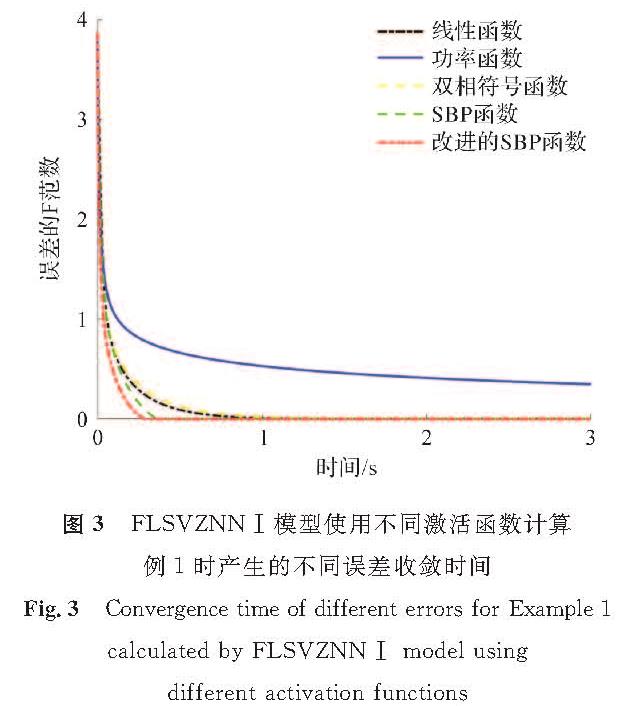
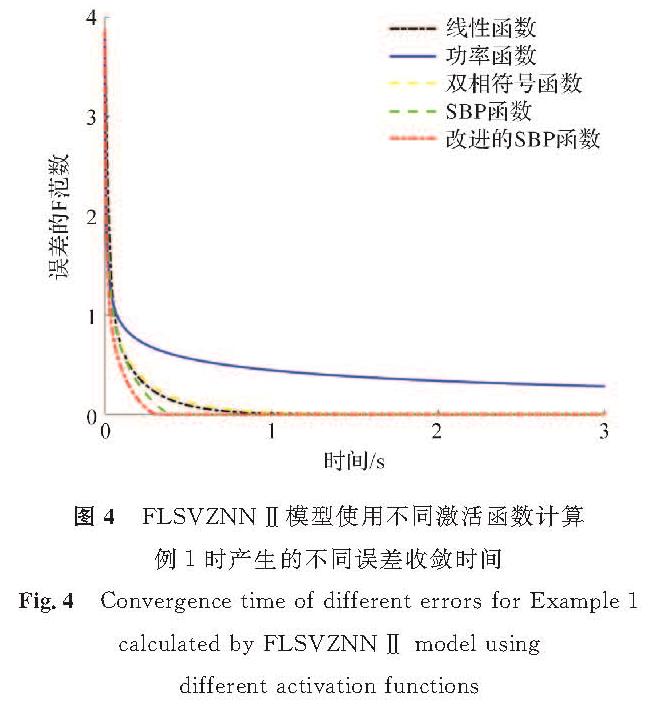
FLSVZNN-Ⅰ模型、FLSVZNN-Ⅱ模型使用不同激活函数计算例1时产生的不同误差收敛时间分别如图3和图4所示。可知,当使用多种激活函数来激活FLSVZNN模型时,尽管FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型存在差异,但都能在不同的激活函数下使误差函数收敛,这验证了两种处理方法求解复数西尔维斯特方程的有效性。此外,由图3和图4可知,当FLSVZNN-Ⅰ模型使用线性函数激活时,计算误差约1.0 s左右收敛至0; 使用功率函数时,无法使其收敛到0; 使用双相符号函数激活时,计算误差约1.0 s左右收敛至0; 使用SBP函数为激活函数时,计算误差至少0.4 s左右收敛至0; 使用改进的SBP激活函数时,计算误差约0.3 s左右收敛至0。FLSVZNN-Ⅱ模型的结果类似。可以得出结论,在收敛速度方面,使用改进的SBP激活函数收敛速度最快。
图3 FLSVZNN-Ⅰ模型使用不同激活函数计算例1时产生的不同误差收敛时间
Fig.3 Convergence time of different errors for Example 1 calculated by FLSVZNN-Ⅰ model using different activation functions
图4 FLSVZNN-Ⅱ模型使用不同激活函数计算例1时产生的不同误差收敛时间
Fig.4 Convergence time of different errors for Example 1 calculated by FLSVZNN-Ⅱ model using different activation functions
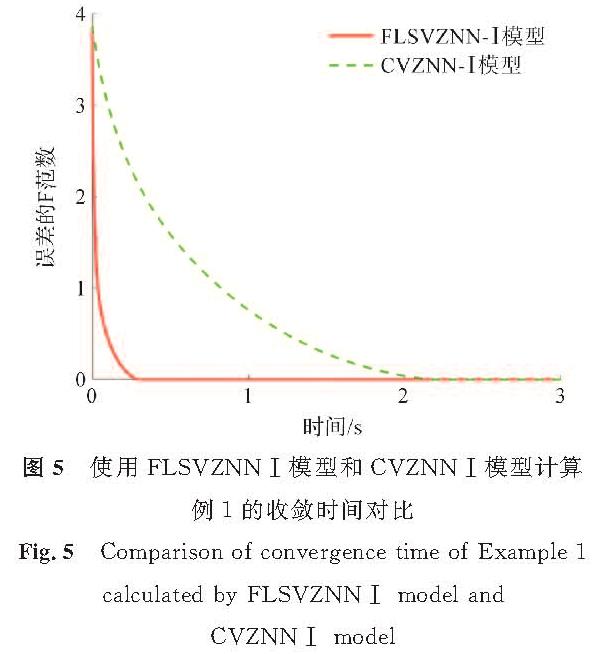
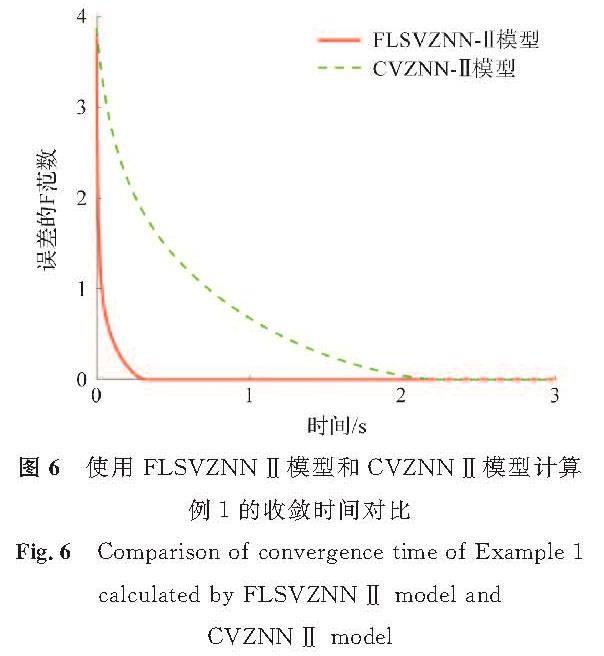
图5和图6分别显示了使用FLSVZNN模型和CVZNN模型计算例1的收敛时间对比,结果进一步验证了FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型在使用改进的SBP激活函数作用下处理复数矩阵的有效性。由图5可知,FLSVZNN-Ⅰ模型求解的收敛时间约0.3 s; 而CVZNN-Ⅰ模型求解的收敛时间至少2.2 s。可见在收敛速度方面,FLSVZNN-Ⅰ模型明显优于CVZNN-Ⅰ模型。FLSVZNN-Ⅱ模型的结果类似。这验证了在CVZNN神经网络加入模糊逻辑系统产生的模糊参数v后,生成的两个FLSVZNN模型性能更优。
图5 使用FLSVZNN-Ⅰ模型和CVZNN-Ⅰ模型计算例1的收敛时间对比
Fig.5 Comparison of convergence time of Example 1 calculated by FLSVZNN-Ⅰ model and CVZNN-Ⅰ model
图6 使用FLSVZNN-Ⅱ模型和CVZNN-Ⅱ模型计算例1的收敛时间对比
Fig.6 Comparison of convergence time of Example 1 calculated by FLSVZNN-Ⅱ model and CVZNN-Ⅱ model
例2 考虑了具有系数U(t)、V(t)、W(t)的复数时变西尔维斯特方程:
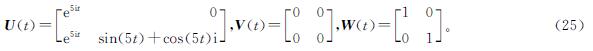
求解可知:例2的U(t)的特征值λ1=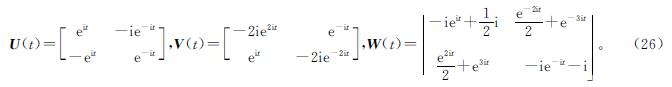 ,λ2=
,λ2=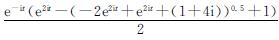 ; V(t)的特征值λ1=-2ie2it-1,λ2=1-2ie2it。U(t)和-V(t)同样没有共同的特征值,满足X(t)是唯一解。
; V(t)的特征值λ1=-2ie2it-1,λ2=1-2ie2it。U(t)和-V(t)同样没有共同的特征值,满足X(t)是唯一解。
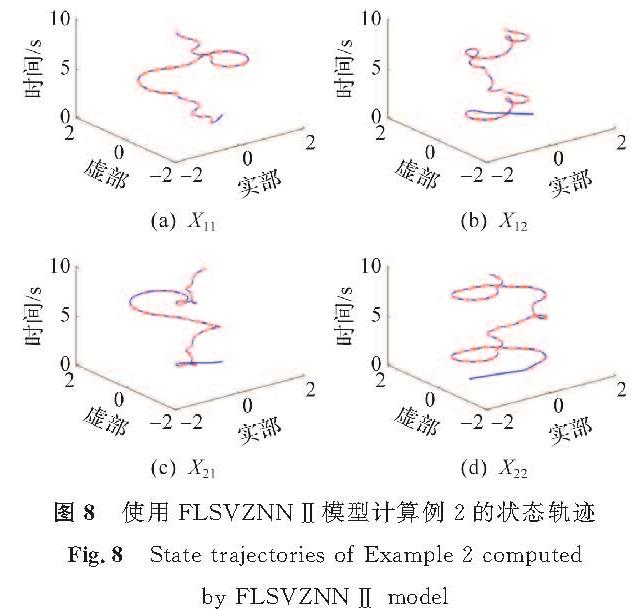
使用FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型求解例2的状态轨迹,分别如图7和图8所示。
由图7和图8可知,这两种模型都可以在激活函数Ω(x)=x下,从一个特定的初始状态X(0)=[1,1; 1,-1]开始,使复数矩阵X(t)从用实心蓝线表示的状态解收敛到用红色虚线表示的理论解,有较好的收敛性能。
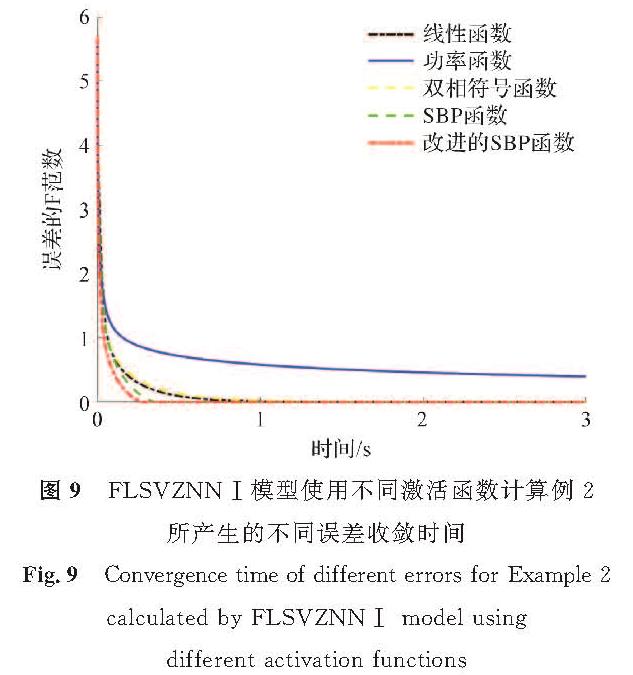
图9和图 10分别为FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型使用不同激活函数计算例2所产生的不同误差收敛时间。由图9和图 10可知,当使用多种激活函数来激活FLSVZNN模型时,尽管FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型存在差异,但都能在不同的激活函数下使误差函数收敛,这进一步验证了两种处理方法求解复数西尔维斯特方程的有效性。此外,由图9和图 10还知,当FLSVZNN-Ⅰ模型使用线性函数激活时,计算误差约0.8 s左右收敛至0; 使用功率函数时,无法使其收敛至0; 使用双相符号函数激活时,计算误差约0.8 s左右收敛至0; 使用SBP函数为激活函数时,计算误差约0.3 s左右收敛至0; 使用改进的SBP激活函数时,计算误差约0.3 s左右收敛至0。FLSVZNN-Ⅱ模型的结果类似。可见,在收敛速度方面,使用改进的SBP激活函数最快。
图9 FLSVZNN-Ⅰ模型使用不同激活函数计算例2所产生的不同误差收敛时间
Fig.9 Convergence time of different errors for Example 2 calculated by FLSVZNN-Ⅰ model using different activation functions
图 10 FLSVZNN-Ⅱ模型使用不同激活函数计算例2所产生的不同误差收敛时间
Fig.10 Convergence time of different errors for Example 2 calculated by FLSVZNN-Ⅱ model using different activation functions
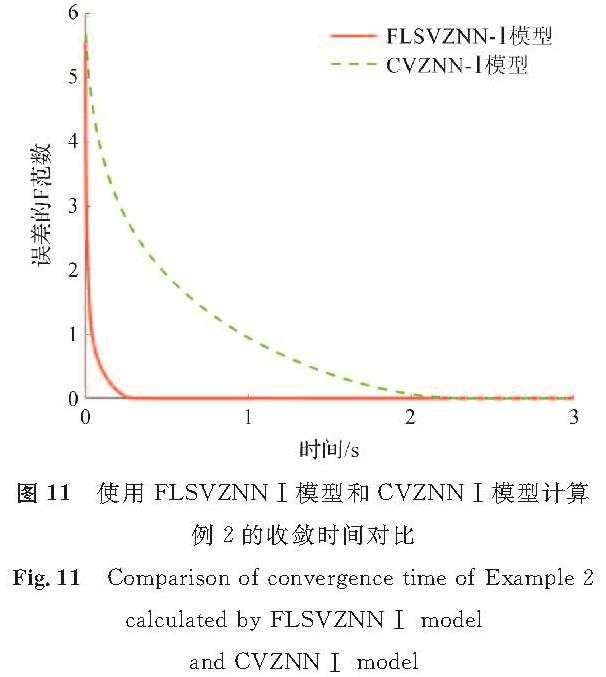
图 11和图 12分别显示了使用FLSVZNN模型和CVZNN模型计算例2的收敛时间对比。
图 11 使用FLSVZNN-Ⅰ模型和CVZNN-Ⅰ模型计算例2的收敛时间对比
Fig.11 Comparison of convergence time of Example 2 calculated by FLSVZNN-Ⅰ model and CVZNN-Ⅰ model
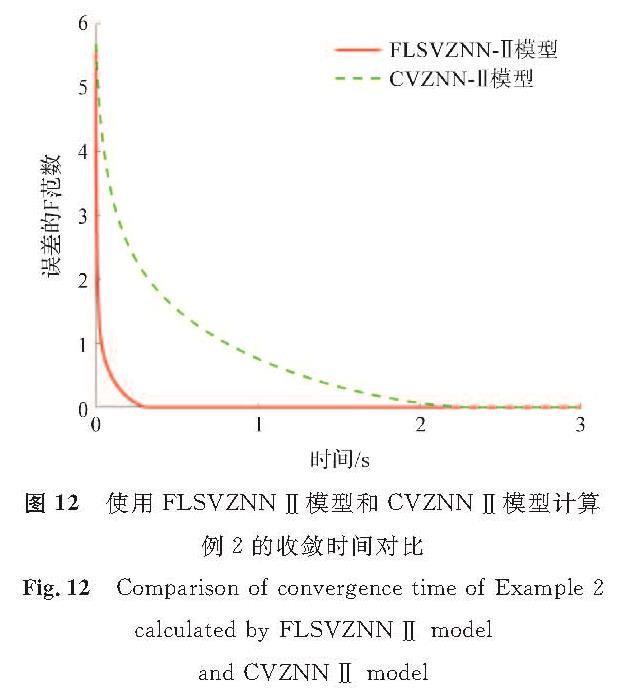
图 12 使用FLSVZNN-Ⅱ模型和CVZNN-Ⅱ模型计算例2的收敛时间对比
Fig.12 Comparison of convergence time of Example 2 calculated by FLSVZNN-Ⅱ model and CVZNN-Ⅱ model
图 11和图 12的结果进一步验证了FLSVZNN-Ⅰ模型和FLSVZNN-Ⅱ模型在改进的SBP激活函数作用下处理复数矩阵的有效性。由图 11可知,FLSVZNN-Ⅰ模型求解的收敛时间约0.3 s; 而CVZNN-Ⅰ模型求解的收敛时间至少2.3 s。可见在收敛速度方面,FLSVZNN-Ⅰ模型明显优于CVZNN-Ⅰ模型。FLSVZNN-Ⅱ模型的结果类似。这验证了在CVZNN神经网络加入模糊逻辑系统产生的模糊参数v后,两个FLSVZNN模型相对于两个CVZNN模型性能更优。
FLSVZNN模型在不同激活函数作用下的收敛时间见表1。
表1 FLSVZNN模型在不同激活函数作用下的收敛时间
Table 1 Convergence time of FLSVZNN models under different activation functionss
4 结 语
本研究针对求解时变复数西尔维斯特方程的问题,提出了两种新型的复值模糊神经网络。根据李亚普诺夫定理,对这两种FLSVZNN模型的收敛性能进行了理论分析,并计算了FLSVZNN模型和CVZNN模型的收敛速度,验证了FLSVZNN模型求解的有效性和可行性。最后由数值仿真可知,与传统的激活函数相比,使用改进的SBP函数来激活的两种FLSVZNN模型,收敛速度更快。
- [1] XIAO L, LIAO B, LI S, et al. Nonlinear recurrent neural networks for finite-time solution of general time-varying linear matrix equations[J]. Neural Networks,2018,98:102.
- [2] XIAO L, ZHANG Z, ZHANG Z, et al. Design, verification and robotic application of a novel recurrent neural network for computing dynamic Sylvester equation[J]. Neural Networks,2018,105:185.
- [3] DAHIPHALE V, BANSOD G, ZAMBARE A, et al. Design and implementation of various datapath architectures for the ANU lightweight cipher on an FPGA[J]. Frontiers of Information Technology and Electronic Engineering,2020,21(4):615.
- [4] SHEN Y, MIAO P, HUANG Y, et al. Finite-time stability and its application for solving time-varying Sylvester equation by recurrent neural network[J]. Neural Processing Letters,2015,42(3):767.
- [5] WANG J. Recurrent neural networks for computing pseudoinverses of rank-deficient matrices[J]. SIAM Journal on Scientific Computing,1997,18(5):1479.
- [6] WANG X, CHE M, WEI Y. Recurrent neural network for computation of generalized eigenvalue problem with real diagonalizablematrix pair and its applications[J]. Neurocomputing,2016,216:230.
- [7] ZHANG Z, KONG L, ZHENG L, et al. Robustness analysis of a power-type varying-parameter recurrent neural network for solving time-varying QM and QP problems and applications[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems,2020,50(12):5106.
- [8] LI W, MA X, LUO J, et al. A strictly predefined-time convergent neural solution to equality- and inequality-constrained time-variant quadratic programming[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems,2021,51(7):4028.
- [9] YU F, LIU L, XIAO L, et al. A robust and fixed-time zeroing neural dynamics for computing time-variant nonlinear equation using a novel nonlinear activation function[J]. Neurocomputing,2019,350:108.
- [10] PANDE A, GOEL V. Complex-valued neural network in image recognition:a study on the effectiveness of radial basis function[J].World Academy of Science,Engineering and Technolog,2007,26:220.
- [11] ZHANG Y, ZHAN L, LI K. Complex-valued Zhang neural network for online complex-valued time-varying matrix inversion[J]. Applied Mathematics & Computation,2011,217(24):10066.
- [12] 孔颖,孙明轩.Sylvester时变矩阵方程求解的终态神经网络算法[J].计算机科学,2018,45(10):6.
- [13] LI S, CHEN S, LIU B. Accelerating a recurrent neural network to finite-time convergence for solving time-varying Sylvester equation by using a sign-bi-power activation function[J]. Neural Processing Letters,2013,37(2):189.
- [14] 高畅,孔颖,胡汤珑.基于有限时间神经网络求解的时变复数矩阵方程[J].浙江科技学院学报,2022,34(5):409.
- [15] 石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.
- [16] 孟廷豪.基于模糊控制的机器人避障研究[D].太原:中北大学,2013.
- [17] ZHANG Z, YAN Z. An adaptive fuzzy recurrent neural network for solving the nonrepetitive motion problem of redundant robot manipulators[J]. IEEE Transactions on Fuzzy Systems,2020,28(4):684.
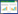 图 1 使用FLSVZNN-Ⅰ模型计算例1的状态轨迹
Fig.1 State trajectories of Example 1 computed by FLSVZNN-Ⅰ model
图 1 使用FLSVZNN-Ⅰ模型计算例1的状态轨迹
Fig.1 State trajectories of Example 1 computed by FLSVZNN-Ⅰ model