本文研究以下高阶拟线性波动方程的初边值问题:

式(1)～(3)中:r>2是实数,m≥1是正整数,a>0,b≥0,μ>0及δ>0是常数; Ω∂Rⁿ是具有光滑边界Ω的有界区域; v是∂Ω上的单位外法向量,(∂ⁱu)/(∂vⁱ)表示u的i阶法向导数; D表示梯度算子,即

。

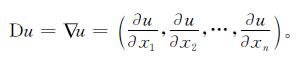此外,当m=2j时,D^mu=^ju; 当m=2j+1时,D^mu=D^ju。

当m=a=1,b=0时,式(1)是具有耗散项的非线性波方程,许多人用不同的方法和技巧对此类方程的Cauchy问题或初边值问题进行了研究,得到了整体解的存在唯一性及衰减估计,并建立了解的爆破性质,如文献[1-4]。在a,b>0的情况下,Ikehata^[5]证明了如果初值{u₀,u₁}属于稳定集,并且足够小,则式(1)～(3)存在整体强解。

当m>1,a,b>0时,式(1)具有明确的物理背景,它描述了受Kelvin-Voig型内部材料阻尼项和线性阻尼项μu_t影响的Woinowsky-Krieger型振动梁模型^[6-7]。若a=0,b>0,Li^[8]和Ye^[9]研究了带有非线性耗散项的式(1)的初边值问题,并得到了如下结果:r>2时解整体存在; r<2时对于任意的负初始能量,解在有限时间内发生爆破。之后,Messaoudi等^[10]改进了文献[8]中的结论,并且证明了当初始能量有上界时与文献[8]有相同的结果。同时,Galaktionov等^[11]证明了μ=0时,式(1)的Cauchy问题整体解的存在性和不存在性。然而,他们的处理方法不能应用于式(1)～(3)。文献[12-15]研究了更广泛的Kirchhoff型方程及方程组的初边值问题,证明了其局部解和整体解的存在性与不存在性,并建立了整体解的长时间行为。

本文采用常用的记号,H^m(Ω)表示通常数量积和范数意义下的Sobolev空间,H^m₀(Ω)表示C^∞₀(Ω)在H^m(Ω)中的闭包。为简便起见,用||·||_s表示Lebesgue空间L^s(Ω)范数,||·||表示L²(Ω)范数,用等价范数||D^m·||代替H^m₀(Ω)的范数||·||_H^m0(Ω)。C_i(i=1,2,…)表示依赖于已知常数的正常数,并且每次出现时都不相同。

定义式(1)～(3)解的能量如下:

式(4)中:u∈H^m₀(Ω); t≥0。

初始总能量为

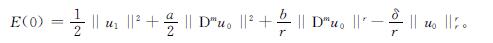
引理1^[16-17] 设s满足:当n≤2m时,2≤s<+∞; 当n>2m时,2≤s<(2n)/(n-2m)。则存在依赖于Ω和s的常数B₁,使得

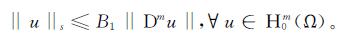
引理2(Young不等式)设X,Y和ε是正常数,并且ξ,ζ≥1,1/ξ+1/ζ=1,则

引理3 令u(t)是式(1)～(3)的解,则t>0时,E(t)是非增函数,且

E'(t)=-μ||u_t||²≤0。(5)

证明:在式(1)的两边同乘以u_t,并在Ω×[0,t]上积分,由分部积分得

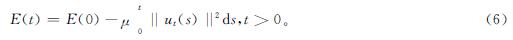
由此可知,E(t)是可积函数的原函数,故对于任一正则解u(t),能量E(t)关于t绝对连续且满足式(5)。因此,由稠密性原理知,结论成立。

定理1～2给出式(1)～(3)局部解和整体解的存在性结果,其证明过程参见文献[5]。

定理1(局部存在性)设a>0,b≥0,μ>0,δ>0。当n≤2m时,2≤r<+∞; 当n>2m时,2≤r<(2n)/(n-2m)。如果初值(u₀,u₁)∈(H^2m(Ω)∩H^m₀(Ω))×H^m₀(Ω),则存在T>0使得式(1)～(3)存在唯一的局部解u(x,t),并满足

u(x,t)∈C([0,T]; H^2m(Ω)∩H^m₀(Ω))∩C¹([0,T); H^m₀(Ω))∩C²([0,T); L²(Ω))。

此外,下式成立

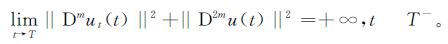
定理2(整体存在性)设a>0,b≥0,μ>0,δ>0。当n≤2m时,2≤r<+∞; 当n>2m时,2≤r<(2n)/(n-2m)。进一步假设δB^r₁≤b,如果初值(u₀,u₁)∈(H^2m(Ω)∩H^m₀(Ω))×H^m₀(Ω)满足E(0)≥δ/r||u₀||^r_r及||D^2mu₀||²+||D^mu₀||²<γ,则T=+∞,其中γ>0是常数。

引理4对研究式(1)～(3)整体解的指数衰减估计起着重要的作用。

引理4^[18] 令F:R⁺→R⁺是非增函数,并假设存在常数L>0使得

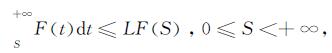
则F(t)≤F(0)e^1-t/L,t≥0。

本文主要结果叙述如下。

定理3 在定理2的假设条件下,式(1)～(3)的整体解有如下指数衰减估计:

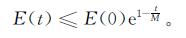
式中M>0是常数。

证明:令E(t)=E(u(t)),如果能够证明整体解的能量满足下列估计

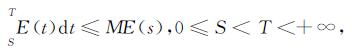
则由引理4可得定理3的结果。

注意到假设条件δB^r₁≤b,由引理1得

由于初值(u₀,u₁)∈(H^2m(Ω)∩H^m₀(Ω))×H^m₀(Ω),所以式(1)～(3)的解具有足够的正则性保证后续计算。式(1)的两边同时乘以u,并在Ω×[S,T]上积分得

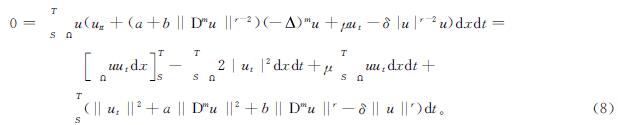
由式(8)知

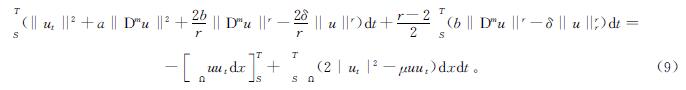
根据式(4)、式(7)和式(9)得

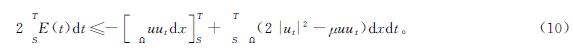
由式(4)和式(7)知E(t)>0。联合引理1,式(4)和Cauchy-Schwarz不等式有

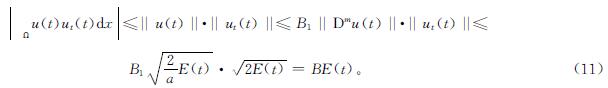
式(11)中:B=(2B₁)/(a^1/2)。

应用式(11)和引理3有

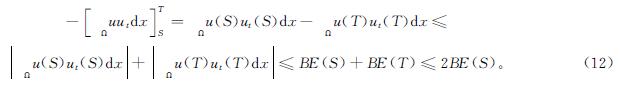
由式(10)和式(12)得

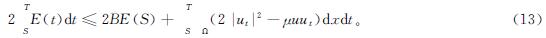
从式(4)、式(5)和引理2可推出

因此,由式(14)知

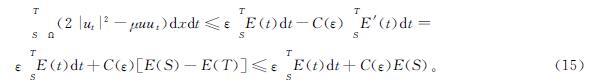
由式(13)和式(15)得

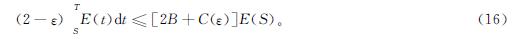
选取ε足够小使得ε<2,则由式(16)知

式(17)中:M=(2B+C(ε))/(2-ε)>0是常数。因此由式(17)及引理4可得如下指数衰减估计:

E(t)≤E(0)e^1-t/M。

定理3证毕。

本文研究了式(1)的初边值问题,在式(1)～(3)解的局部存在(定理1)和整体存在(定理2)的前提条件下,应用Komornik的积分不等式(引理4)、Cauchy-Schwarz不等式及能量估计方法,得到了式(1)～(3)的整体解能量的指数衰减估计(定理3)。