为避免频率和相位估计所带来的误差,研究只根据接收到的信号幅值即信号强度就可以进行振幅估计的算法。针对已知噪声方差的情况,采用最大似然原理推导出含振幅估计的等式,提出了两种迭代算法,并对其平均迭代次数及计算复杂度进行了比较。仿真试验结果显示,两种迭代算法性能几乎相同且均优于传统振幅估计算法,其中牛顿迭代法计算复杂度略高,但其平均迭代次数小于阶梯迭代法,尤其是在低信噪比下。由此可见,基于信号强度的最大似然振幅估计牛顿迭代法优于其他振幅估计算法。
In order to avoid errors introduced by joint estimation of the frequency and phase, amplitude estimation based only on information from the noisy received signal magnitude, is studied in this paper. With regard to the signal with known noise variance, the maximum likelihood estimation is used to derive an equation involving amplitude estimation. Then, two iterative algorithms were proposed to find numerical solutions, while comparing their average number of iterations and computational complexities. Simulation results show that performance of the two iterative algorithms are almost identical and both are superior to conventional counterparts. The computational complexity of the iterative Newton algorithm is slightly higher, but its average number of iterations is smaller than that of iterative step algorithm, especially at low SNR. It can be concluded that iterative Newton's algorithm for maximum likelihood magnitude-based amplitude estimation is superior to other amplitude estimation algorithms.
从一系列信号样本中估计出信号的振幅、频率、相位等未知参数是通信系统中的重要研究内容。目前通信系统中要获得信号的振幅参数,需经过一系列复杂的计算,当且仅当信号的频率参数恢复后,才能得到信号的振幅参数估计[1-2]。不仅如此,频率估计过程复杂、计算困难[3],易出现异常值[4-5]等,其准确度极大地限制了振幅估计的性能。振幅参数的估计性能总是依赖于频率参数估计的性能[6],这对开关键控调制等仅需要振幅参数估计的通信系统而言是需要避免的。因此有必要研究出不受限于频率估计的振幅估计算法。
1954年,Slepian[7]提出了信号的参数估计问题,将费雪与克拉美罗理论应用于经过加性高斯白噪声信道的信号参数估计中,但他的大部分工作都集中在连续时间观测模型上。随后Rife[8]提出了基于离散时间序列,经过加性高斯白噪声信道的信号参数估计方法。然而,其实际算法非常复杂,需要找出基于快速傅里叶变换的频域解。Sijbers[9]357提出了莱斯分布参数估计的最大似然算法,但并未给出振幅估计子模型。本文假设对信号的振幅、频率、相位参数没有任何先验知识,即振幅可能是任意的非负值,频率和相位可能是区间[-π,π)之间的任意取值,则最合适的参数估计方法是最大似然估计[4]。一般通过利用接收信号的幅度和相位,样本均值估计子可实现克拉美-罗下界[10]。然而,只有接收信号的幅值时,样本均值估计子并非最优。矩量法是一种常用的估计方法,因为n次方样本均值是n阶矩的无偏估计[11],所以用n次方样本均值即可逼近莱斯分布的n阶矩。例如,传统的均方根振幅估计子是利用二次样本均值逼近二阶矩,但其性能还有待优化。
本文研究基于信号强度的振幅估计问题,该问题等价于经典的莱斯分布参数估计[12]问题。本研究结果不仅能够应用于通信领域,如通信信号强度测距[13]、信道建模[14-15]等,还能够应用于磁共振成像[16-18]、语音处理[19]、雷达[20]等领域。
1 信号模型通信系统的接收信号是一种可用复数表示且包含复加性高斯白噪声的信号r(k),信号模型[21]为
r(k)=Aej(ω k+θ)+n(k),k=0,1,2,…。(1)
式(1)中:r(k)为接收信号; A为发送信号的实际振幅,可以是任意非负实数; ω与θ分别为信号的频率与相位; n(k)为一种圆对称、独立同分布的复加性高斯白噪声,其均值为零,方差为2σ2。
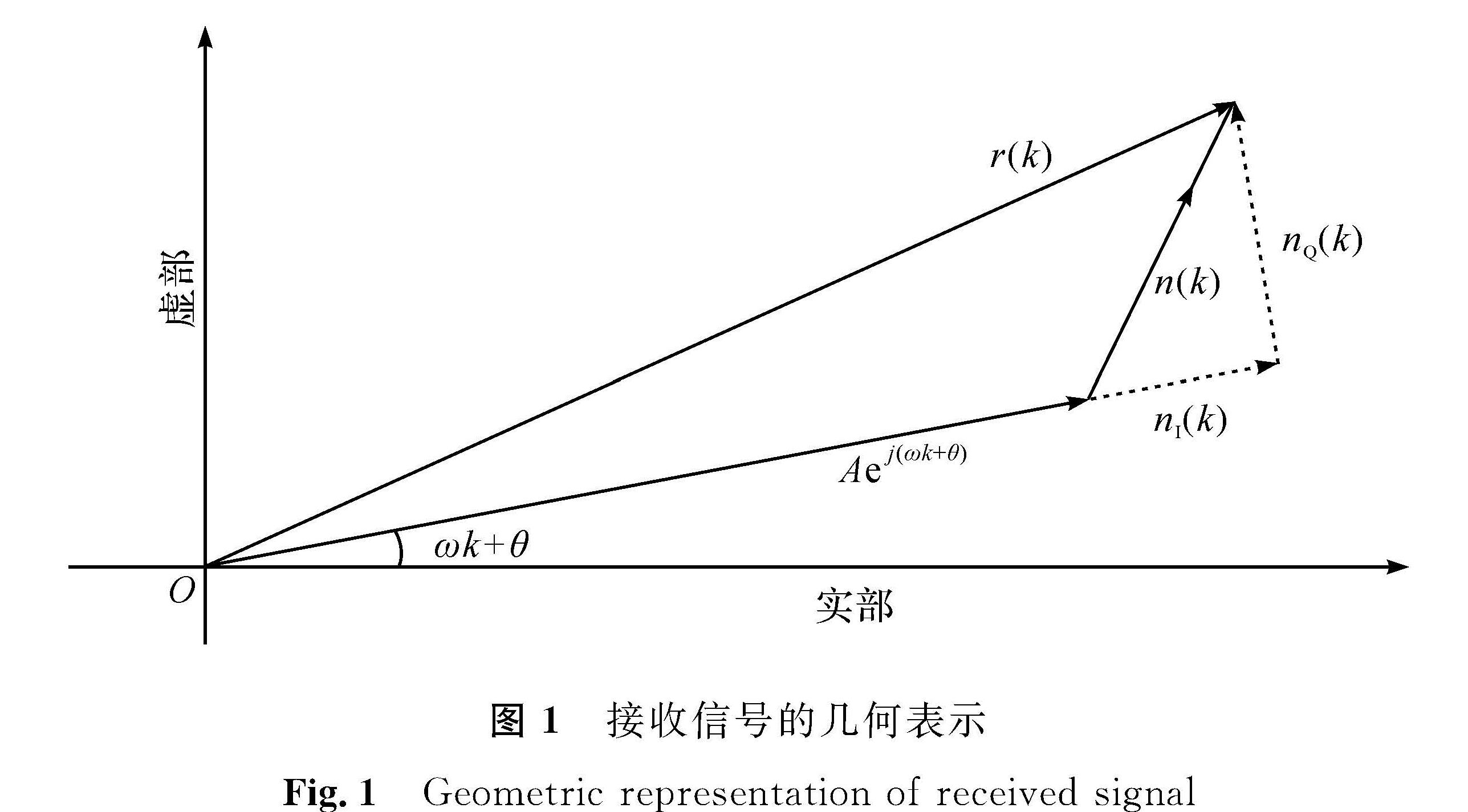
接收信号的几何相量表示方法如图1所示。n(k)被分解为平行于Aej(ω k+θ)的同相分量nI(k)和垂直于Aej(ω k+θ)的正交分量nQ(k)。
由于n(k)是圆对称的,且nI(k)和nQ(k)两个正交分量在统计学上是独立同分布的高斯随机变量,所以从图1可以看出新建立的坐标系即为原坐标系逆时针旋转角度ωk+θ,故信号模型为
r(k)=A+nI(k)+jnQ(k)。(2)
该模型也适用于恒定传输信号的情况。在新建立的坐标系中,r(k)模值为
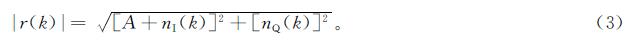
r(k)的值为复数,故理论上有3种不同的样本均值估计子,即取复数、实部或模值,可以分别表示为ASMc、ASMr和ASMm。这取决于接收机接收到的r(k)样本值。本文信噪比公式定义为γ=A2/2σ2,估计性能使用均方误差(mean square error,MSE)进行评价,定义如下:
E{|A-A|2}=1/T∑T|A-A|2。(4)
式(4)中:T为估计次数; A为振幅估计值。
当可以得到r(k)的复数值即通过相干检测得到的r(k)时,估计子
ASMc=1/N∑N-1k=0r(k)。(5)
式(5)中:N为数据样本数量。此估计子的克拉美-罗下界(Cramér-Rao lower bound,CRLB)为2σ2/N。
当可以采集到复数r(k)的实部为样本时,即消除了虚部,使噪声功率降低了一半,估计子
ASMr=1/N∑N-1k=0R[r(k)]。(6)
式(6)中:R[·]表示取实部。此类接收机为最佳接收机,此估计子的均方误差等于其克拉美-罗下界[11],ACRLB=σ2/N,是3种样本均值估计子中最小的一种。
当只能检测信号r(k)的幅度值即信号强度时,估计子
ASMm=1/N∑N-1k=0|r(k)|。(7)
ASMc和ASMr都需要相干接收,不适用于本文考虑的场景。因此,本文将基于接收信号强度|r(k)|的估计子ASMm与我们提出的估计子进行性能比较。
2.2 均方根估计数量为N的样本均方值为
A2M=1/N∑N-1k=0|r(k)|2。
很明显,E[A2M]=E[|r(k)|2]。任意随机变量的二阶矩满足E[|r(k)|2]=A2+2σ2[14],因此E[A2M]=A2+2σ2。E[A2M]与A2M近似相等,可得
A2M=A2+2σ2。
因此可得到传统的均方根振幅估计子

信号强度|r(k)|是服从莱斯分布的随机变量,其条件概率密度函数[9]357
p(|r(k)||A,σ2)=(|r(k)|)/(σ2)exp(-(|r(k)|2+A2)/(2σ2))I0((|r(k)|A)/(σ2))。(9)
式(9)中:I0(·)为零阶第一类修正贝塞尔函数。由p(|r(k)||A,σ2)可知接收信号模值的联合条件概率密度函数
p({|r(k)|}N-1k=0|A,σ2)=∏N-1k=0p(|r(k)||A,σ2)=∏N-1k=0(|r(k)|)/(σ2)exp(-(|r(k)|2+A2)/(2σ2))I0((|r(k)|A)/(σ2))。(10)
式(10)中:N为信号强度样本数量。式(10)的似然函数
Λ(A,σ2)=lnp({|r(k)|}N-1k=0|A,σ2)=∑N-1k=0[ln(|r(k)|)/(σ2)-(|r(k)|2+A2)/(2σ2)+lnI0((|r(k)|A)/(σ2))]。
假设接收机的噪声方差σ2已知,或已通过某种噪声方差估计方法估计得到相对准确的σ2,就能够凭借最大似然原理估计振幅A。将似然函数Λ(A,σ2)取对数求偏导,得到取极大值条件下的对数似然方程,即需要满足
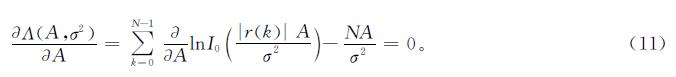
根据第一类修正贝塞尔函数性质d/(dx)[x-vIv(x)]=x-vIv+1(x),进一步化简式(11),整理可得关于A的表达式[9]359
A=1/N∑N-1k=0|r(k)|(I1((|r(k)|A)/(σ2)))/(I0((|r(k)|A)/(σ2)))。(12)
式(12)中:I1(·)为一阶第一类修正贝塞尔函数。式(12)即为利用最大似然估计得到的振幅估计隐函数,该隐式解即为基于信号强度恢复信号的振幅信息。由于无法直接解得其值,因此需运用迭代算法求解。
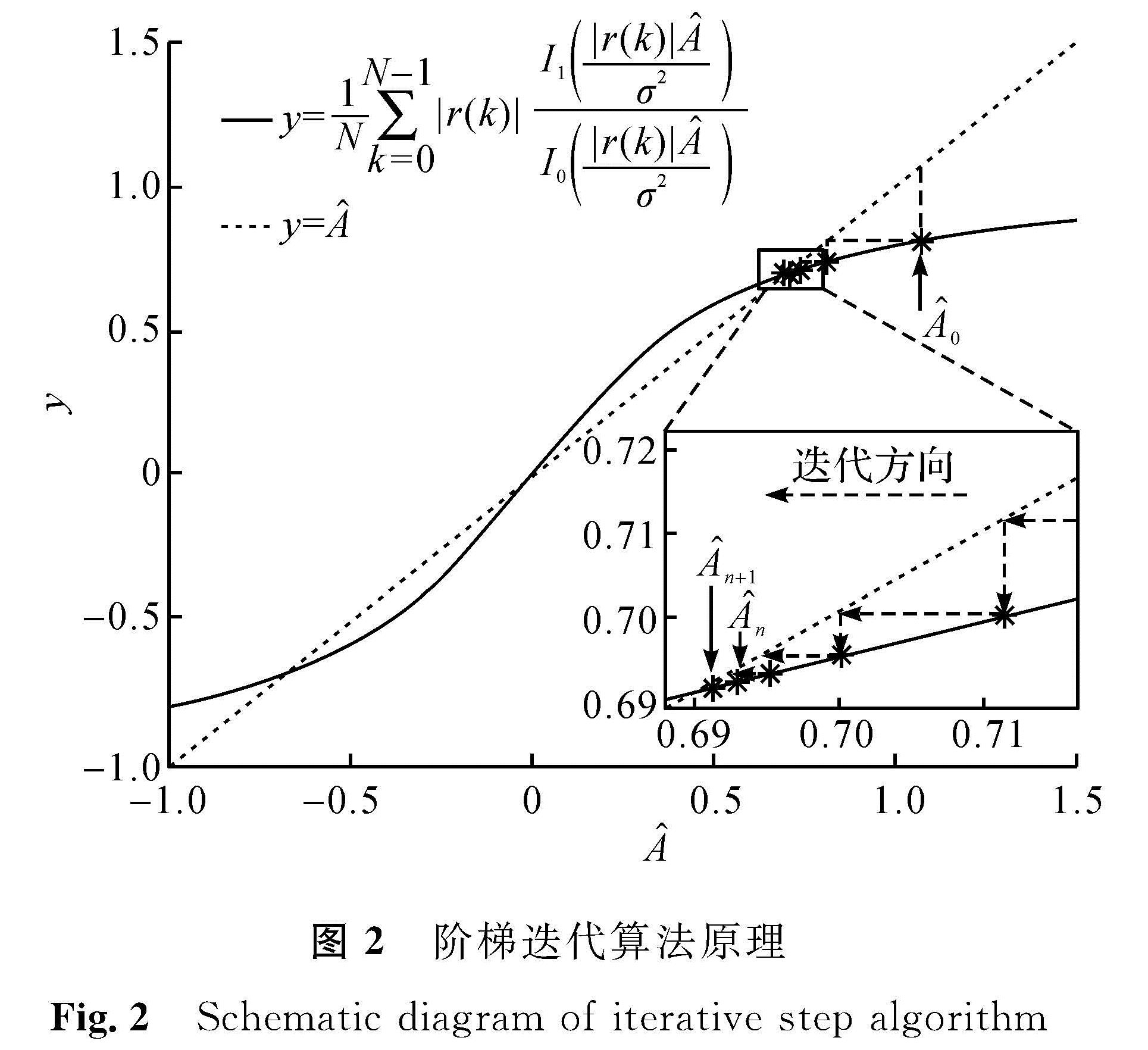
3.2 迭代算法3.2.1 阶梯迭代法设An为第n次迭代得到的振幅估计值。使用传统的样本均值估计子ASMm作为迭代初值A0,即A0=ASMm。根据最大似然振幅估计表达式(12),可以得到第n+1次迭代得到的振幅估计子
An+1=1/N∑N-1k=0|r(k)|(I1((|r(k)|An)/(σ2)))/(I0((|r(k)|An)/(σ2))),n=0,1,2,…。(13)
最终,当迭代增量低于阈值ε时,即满足|An+1-An|<ε,停止迭代,An+1即为阶梯迭代法的估计子AS。
阶梯迭代算法原理如图2所示,实线与点线分别为式(13)右边与左边,*代表An,带箭头虚线表示在迭代过程中初始点A0沿着箭头方向移动逼近至解An+1的轨迹。实线与点线存在3个交点,表示式(13)的3个解,即1个正解、1个对称负解和1个零解。在这3种情况中,显然正解是本文所需解。I1(x)/I0(x)是关于x的递增函数,式(13)随A增大而单调递增,又由于对所有x>0都有I1(x)/I0(x)<1,根据式(7)和式(13)显然可以得到ASMm>An+1,即初始点A0总是在包括最终解An+1所有后续迭代估计子的右边。因此,阶梯迭代算法的估计子总是单调向左移动,即图2中迭代方向,迭代结果An+1随着迭代次数n的增大而减小,最终逼近正解。
3.2.2 牛顿迭代法牛顿迭代法是寻找方程近似根的一种快速收敛算法。同样使用传统的样本均值估计子ASMm作为迭代初值A0,即A0=ASMm。根据最大似然振幅估计表达式(12),可以得到第n+1次迭代得到的振幅估计子
An+1=An-(f(An))/(f'(An))。(14)
式(14)中:
f(An)=An-1/N∑N-1k=0|r(k)|(I1((|r(k)|An)/(σ2)))/(I0((|r(k)|An)/(σ2))),
f'(An)=1-1/N∑N-1k=0(|r(k)|2)/(σ2)[1-((I1((|r(k)|An)/(σ2)))/(I0((|r(k)|An)/(σ2))))/((|r(k)|An)/(σ2))-(I21((|r(k)|An)/(σ2)))/(I20((|r(k)|An)/(σ2)))]。(15)
最终,当迭代增量低于阈值ε时,即满足|An+1-An|<ε,停止迭代,An+1即为牛顿迭代法的估计子ANt。
牛顿迭代算法原理如图3所示。与阶梯迭代算法同理可证,初始点在正解的右边,在正解至初始点区间内,式(14)曲线单调递增,带箭头虚线表示在迭代过程中初始点A0沿着箭头方向往左移动逼近至解An+1的轨迹。显然,沿着切线移动要比沿着水平阶梯移动快得多。因此,牛顿迭代算法迭代速度远远快于阶梯迭代算法,但由式(15)可看出,其代价是更高的计算复杂度。
4 性能仿真分析本文将实际振幅设置为A=1,噪声方差σ2随信噪比变化,并产生T=106个估计值来评价均方误差性能。仿真结果表明,当A2M<2σ2时,式(12)有可能存在
图4 γ=0 dB,N=10时仅含唯一解的牛顿迭代算法原理
Fig.4 Schematic diagram of A with known σ2using the iterative Newton's algorithm with only one solution with γ=0 dB and N=10
仅有一零解现象。如图4所示,本文以γ=0 dB,N=10时仅含唯一解的牛顿迭代算法原理图为例进行分析。由于只有1个零解,无论初始点如何选择,该算法都明显逼近于零。这是由于存在过大的噪声,导致零为最大似然振幅估计式(12)的唯一解。无论如何修改初始点,都无法提高迭代算法性能。这种情况在低信噪比、较小N的情况下发生概率更大,阶梯迭代算法也同样如此。
传统估计与迭代估计均方误差性能比较如图5所示。在已知噪声方差情况下且阈值均为ε=10-6,阶梯迭代算法与牛顿迭代算法具有相同的均方误差性能。仿真结果与预期一致,两种迭代算法的性能均随着样本数量N的增加而提高,且均在所有信噪比上优于传统振幅估计ASMm和ARMS,并且随信噪比增加逐渐逼近克拉美-罗下界。
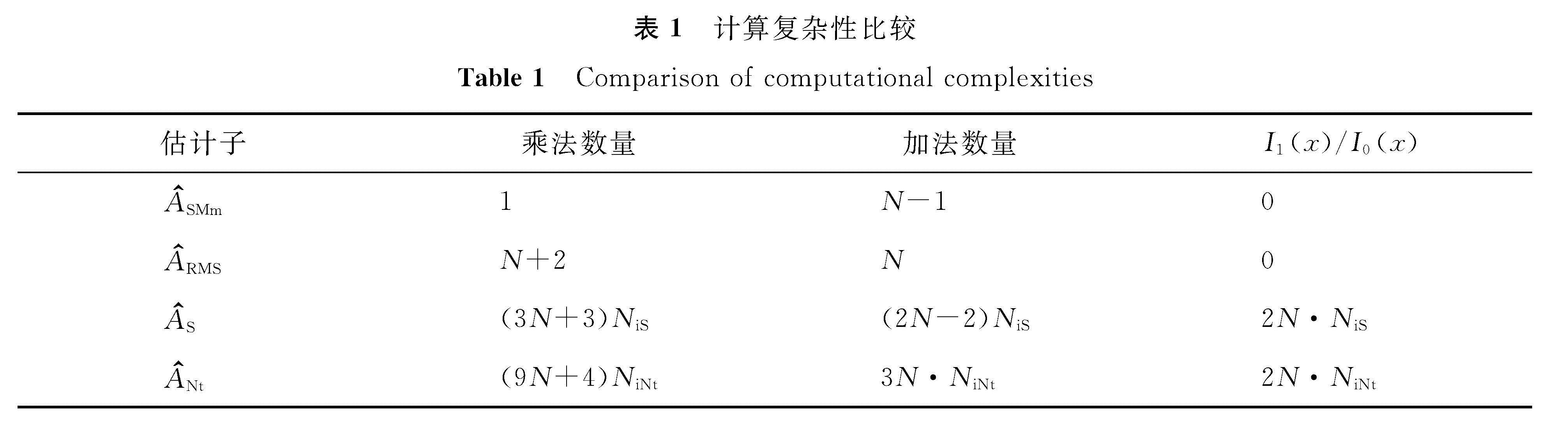
平均迭代次数的比较如图6所示,牛顿迭代算法的迭代速度远远高于阶梯迭代法。然而,对于每次迭代,牛顿迭代算法的计算复杂度较高,如表1所示,其中,NiS和NiNt分别为阶梯迭代算法与牛顿迭代算法的迭代次数。
图6 阶梯迭代估计与牛顿迭代估计平均迭代次数比较
Fig.6 Comparison of average numbers of iterations for iterative step algorithm and iterative Newton's algorithm
5 结 语
本文研究了在无需频率和相位估计的情况下,仅利用接收信号的幅值估计发送信号的实际幅值问题,以及基于已知噪声方差情况下,最大似然幅度估计的两种迭代解法。结果表明,两种迭代算法具有相同的均方误差性能,均优于传统估计算法。本文所分析的问题是典型的莱斯分布参数估计问题的一个典型例子,研究结果可在生物工程、语音处理、雷达、测距、信道建模等领域应用。
- [1] REN J, DAI X, WANG N, et al. Parameters estimation of noise amplitude modulation signal[J].Iet Radar Sonar and Navigation,2017,11(1):161.
- [2] LI Y, WU M, DU X, et al. Nonlinear phase noise tolerance for coherent optical systems using soft-decision-aided ML carrier phase estimation enhanced with constellation partitioning[J].Optics Communications,2018,409(Supplement C):45.
- [3] CHEN Y, BLUM R S. On the impact of unknown signals on delay, doppler, amplitude and phase parameter estimation[J].IEEE Transactions on Signal Processing,2018,67(2):431.
- [4] RIFE D C, BOORSTYN R R. Single-tone parameter estimation from discrete-time observations[J].IEEE Transactions on Information Theory,1974,20(5):591.
- [5] FU H, KAM P. Phase-based, time-domain estimation of the frequency and phase of a single sinusoid in AWGN: the role and applications of the additive observation phase noise model[J].IEEE Transactions on Information Theory,2013,59(5):3175.
- [6] TOMAR S, SUMATHI P, TOMAR S, et al. Amplitude and frequency estimation of exponentially decaying sinusoids[J].IEEE Transactions on Instrumentation and Measurement,2017,67(1):229.
- [7] SLEPIAN D. Estimation of signal parameters in the presence of noise[J].Transactions of the IRE Professional Group on Information Theory,1954,3(3):68.
- [8] RIFE D, BOORSTYN R. Single tone parameter estimation from discrete-time observations[J].IEEE Transactions on Information Theory,1974,20(5):591.
- [9] SIJBERS J, DEN DEKKER A J, SCHEUNDERS P, et al. Maximum-likelihood estimation of Rician distribution parameters[J].IEEE Transactions on Medical Imaging,1998,17(3):357.
- [10] VAN TREES H L. Detection, estimation, and modulation theory, part I: detection, estimation, and linear modulation theory[M].New York: John Wiley and Sons, Inc.,2004.
- [11] KANIA D, BORKOWSKI J, MROCZKA J. Influence of noise on multifrequency signals for the amplitude and phase estimation in photovoltaic systems with a DSP processor[C]//International Conference on Telecommunications and Signal Processing. Piscataway: IEEE,2018:675.
- [12] NGUYEN H H, NECHIPORENKO T. Quarternary signal sets for digital communications with nonuniform sources[C]//Canadian Conference on Electrical and Computer Engineering. Piscataway: IEEE,2005:2085.
- [13] WANG L, ZAWODNIOK M J. Bias and CRB analysis of LoS-based and RSS-based ranging methods[J].IEEE Transactions on Vehicular Technology,2016,65(11):9085.
- [14] NIELSEN J Ø, PEDERSEN G F. Estimation of Rician channels from indoor measurements at 26 GHz[C]//29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications. Piscataway: IEEE,2018.
- [15] SHI C G, SALOUS S, WANG F, et al. Modified Cramér-Rao lower bounds for joint position and velocity estimation of a Rician target in OFDM-based passive radar networks[J].Radio Science,2017,52(1):15.
- [16] BHUJLE H V, VADAVADAGI B H. NLM based magnetic resonance image denoising: a review[J].Biomedical Signal Processing and Control,2019,47:252.
- [17] SANSONE M, FUSCO R, PETRILLO A. D-optimal design of b-values for precise intra-voxel incoherent motion imaging[J].Biomedical Physics and Engineering Express,2019,5(3):1.
- [18] HUANG H M, LIN C. A kernel-based image denoising method for improving parametric image generation[J].Medical Image Analysis,2019,55:41.
- [19] XIE D, ZHANG W. Estimating speech spectral amplitude based on the Nakagami approximation[J].IEEE Signal Processing Letters,2014,21(11):1375.
- [20] GAO C, ZHOU H, WU R, et al. Parameter estimation and multi-pulse target detection of MIMO radar[C]//Region 10 Conference. Piscataway: IEEE,2017:909.
- [21] SIMON M K, ALOUINI M S. Digital communication over fading channels[M].New York: John Wiley and Sons, Inc.,2005.
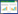 图 1 接收信号的几何表示
Fig.1 Geometric representation of received signal
图 1 接收信号的几何表示
Fig.1 Geometric representation of received signal