图 1 AlexNet网络结构
Fig.1 AlexNet network architecture
表 1 MINIST数据集不同分布的训练数据
Table 1 MINIST training data with different distribution张
MA Jun,QIAN Yaguan,GUO Yankai,et al.Influence upon and improved algorithm of convolutional neural networks under data imbalance[J].2020,(03):-.[doi: 10.3969/j.issn.1671-8798.2020.03.004]
[PDF全文]
通过不同的数据分布、激活函数和网络结构对卷积神经网络(convolutional neural networks,CNN)的训练过程进行试验分析发现,数据不均衡会造成CNN训练过程收敛慢、泛化能力差的负面影响。针对这一问题,结合过抽样和欠抽样各自的优点,在随机梯度下降算法的基础上,提出均衡小批量随机梯度下降算法(equilibrium mini-batch stochastic gradient descent,EMSGD),保证小批量内的数据均衡,精确调整更新参数的梯度方向。试验结果表明,均衡小批量随机梯度下降算法可以在数据不均衡条件下提高CNN训练误差收敛速度,提高泛化性能。
Experiments under different data, activation functions and network structures show that the CNN training error converges slowly and the generalization ability is poor under imbalanced training data. In response to this problem, in combination with advantages of over-sampling and under-sampling, equilibrium mini-batch stochastic gradient descent(EMSGD)was put forward on the basis of the mini-batch stochastic gradient descent, ensuring the data balance in mini-batch and adjusting accurately the gradient direction of update parameters. Experiments prove that EMSGD can raise convergence speed of CNN training error under the condition of imbalanced training data and improve the generalization ability.
随着深度学习的兴起和人工智能第三次浪潮的到来,深度神经网络被成功地应用到图像识别[1-2]、语音识别[3-4]、自然语言处理等领域[5-6]。在2015年ImageNet项目举办的ImageNet大规模视觉识别挑战赛(ImageNet large scale visual recognition challenge,ILSVRC)中,微软研究院团队提出的深度学习模型成功地将图像识别错误率降低到约3.57%,低于人类5.1%的错误率[1]。微软研究院团队的成功极大地激发了科研人员对深度神经网络的研究热情。但在研究过程中我们发现,训练数据不均衡会导致深度卷积神经网络(convolutional neural networks,CNN)难以收敛及泛化能力差等问题。
数据不均衡现象广泛存在于生物医疗[7]、金融[8]、信息安全[9]、工业[10]、计算机视觉[11]等诸多领域。机器学习领域对数据不均衡问题已经做了大量研究[12-13],目前主要有数据层面和算法层面两种解决方法[14]。数据层面主要通过改变训练集的类分布来实现数据均衡,典型的方法有过抽样[15]和欠抽样[16]。过抽样方法首先复制随机抽取的少数类样本,并将复制的样本加入原本的数据集,从而使原本的数据集各类别数据平衡; 与过抽样相反,欠抽样方法将多数类数据从原始数据集中抽离来使原始数据集各类比数据平衡。有研究结果表明:过抽样方法比较稳定有效,但容易引起过拟合[15]; 欠抽样方法的缺点是丢失了多数类的很多重要信息,但在有的情况下欠抽样优于过抽样[16]。算法层面的方法典型的有代价敏感学习[17],通过给多数类和少数类赋予不同的误分类代价,从而改善数据不均衡问题。
数据不均衡不仅对传统分类器的训练造成负面影响,而且对多层感知器同样会影响训练阶段的收敛和测试阶段的泛化[18]。在深度学习中最常用的解决方法仍然是过抽样技术[19-20],此外代价敏感学习也被应用到解决深度神经网络上的数据不均衡问题[21-22]。最新研究提出的神经网络训练方法将网络训练分为2个阶段,先用均衡数据进行训练,再在不均衡数据上对输出层进行微调[23]。总体而言,目前研究人员对深度学习的不均衡问题及其处理方法还没有较为系统的分析,只是使用了一些基于直觉的解决方法和解决传统机器学习不均衡问题的技术。
基于上述研究,本文主要研究不均衡训练数据对CNN的影响,通过试验发现CNN在不同激活函数和不同网络结构情况下用多种类型的不均衡数据进行训练时,均会造成模型训练过程收敛缓慢、模型准确率低的现象。因此,我们提出均衡小批量随机梯度下降算法(equilibrium mini-batch stochastic gradient descent,EMSGD),在每一轮梯度迭代过程中,从每类数据中抽取相同数量的样本组成小批量,从而保证小批量内的数据均衡。试验结果表明,我们提出的方法在CNN中可实现快速收敛并获得更好的泛化能力。
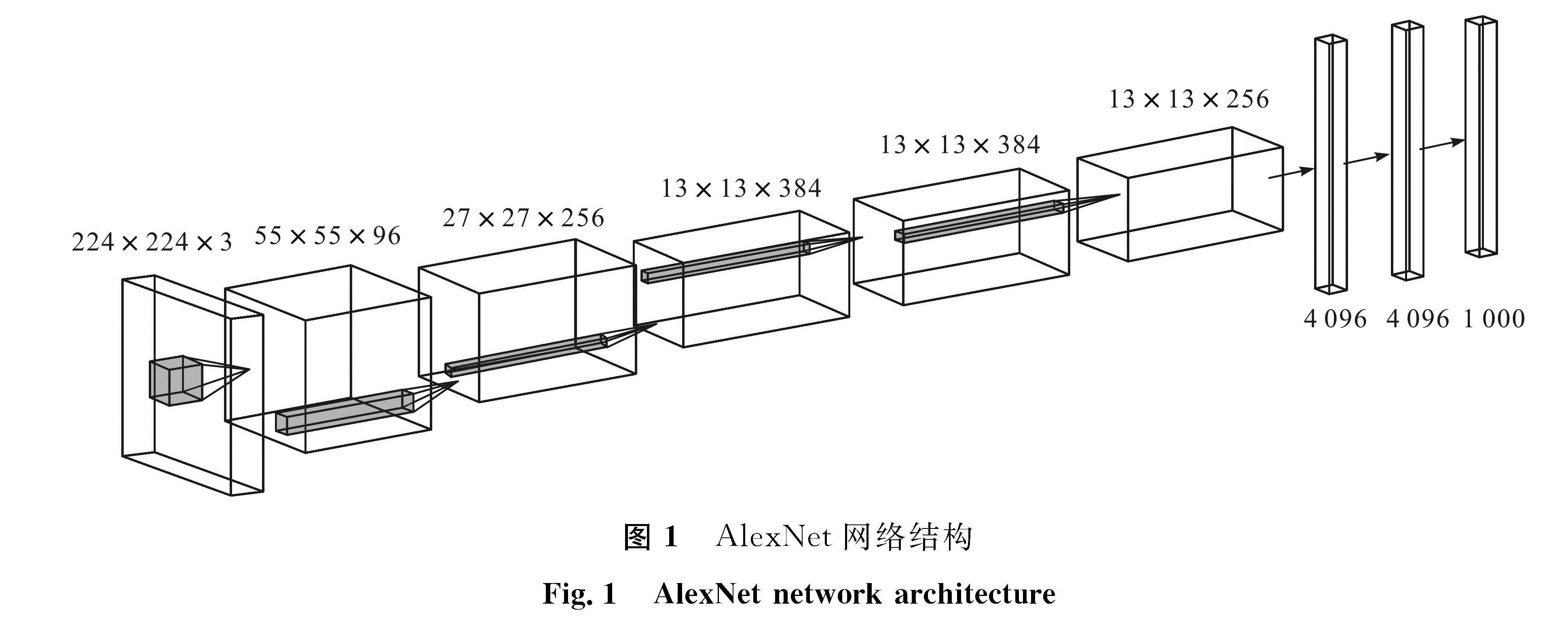
1 理论基础CNN是一类包含卷积计算且具有深度结构的前馈神经网络,在诸多领域特别是在图像相关领域起着重要作用。CNN有多种常用的模型,LeNet-5[24]是最早的CNN模型之一,其结构简单,只有2个卷积层、2个池化层和2个全连接层。虽然其层数较少,但包含了CNN的基本结构,即卷积-池化-全连接的网络结构,为深度卷积神经网络的发展奠定了良好的基础。之后的AlexNet等[2]CNN模型均建立在LeNet-5基础上,同样具有卷积-池化-全连接的网络结构。AlexNet的网络结构如图1所示。
图1 AlexNet网络结构
Fig.1 AlexNet network architecture
1.1 CNN各层作用
卷积层是CNN的核心,其实质是两个矩阵的计算,即代表图像的矩阵和代表卷积核的矩阵之间对应位置相乘再求和。通过激活函数对结果进行非线性变换,以提取图像特征,得到特征图。卷积层通过权重共享减少CNN参数量,便于训练。
池化层又称采样层,一般在卷积层后面,常见的池化运算有最大池化和平均池化。池化操作是将卷积得到的特征图与池化核覆盖区域取平均值或取最大值作为池化结果,具有空间不变性和特征降维的作用,在一定程度上可防止过拟合。卷积和池化一般具有多层,即卷积后进行池化,池化后再卷积,周而复始,以提取原始图像的复杂特征。
多层卷积池化后是全连接层,其作用是将卷积池化层提取到的特征映射到样本的标记空间,对输入样本进行分类。对于多分类问题,最后一层的全连接层一般为Softmax层,即对输出进行Softmax计算,用以输出概率向量,并且计算梯度时更为简单。
1.2 激活函数选择不同的激活函数会影响CNN性能和训练过程,常用的激活函数有Sigmold(S)函数、Tanh(T)函数和Relu(R)函数等,定义如下:
S(z)=1/(1+e-z)。(1)
T(z)=(1-e-2z)/(1+e-2z)。(2)
R(z)={0,z<0;
z,z≥0。(3)
式(1)～(3)中:z为激活函数的输入。S函数和T函数相似,均呈指数形式,但S函数值域为(0,1),T函数为(-1,1)。因为T函数的值关于原点对称,而且幅度要比S函数大,一阶导数也比S函数的更大,所以使用T函数的网络在训练时,收敛速度更快。然而S函数与T函数均存在梯度饱和区,即函数值接近边界时梯度接近0,训练时可能会出现梯度消失问题,导致训练困难。随着神经网络层数的加深,梯度消失问题更容易出现,所以可以避免梯度消失的R函数被更多地应用在具有多层结构的深度神经网络中,例如ResNet[1]、AlexNet[2]等,并且其稀疏性特点可以缓解模型过于复杂时可能会出现的过拟合问题。
2 数据不均衡对CNN的影响为探讨数据不均衡对CNN的影响,抽取MNIST(Mixed National Institute of Standards and Technology)数据集部分数据构建多种不均衡的数据以训练CNN模型,并采用不同的激活函数。试验结果表明,在不同激活函数和网络结构情况下,不均衡训练数据均会对CNN造成不良影响,如对少数类的测试准确率偏低,其总体准确率也低于均衡
图2 MNIST数据集手写体数字实例
Fig.2 Examples of handwritten numerals in MNIST datasets
数据情况下得到的CNN。
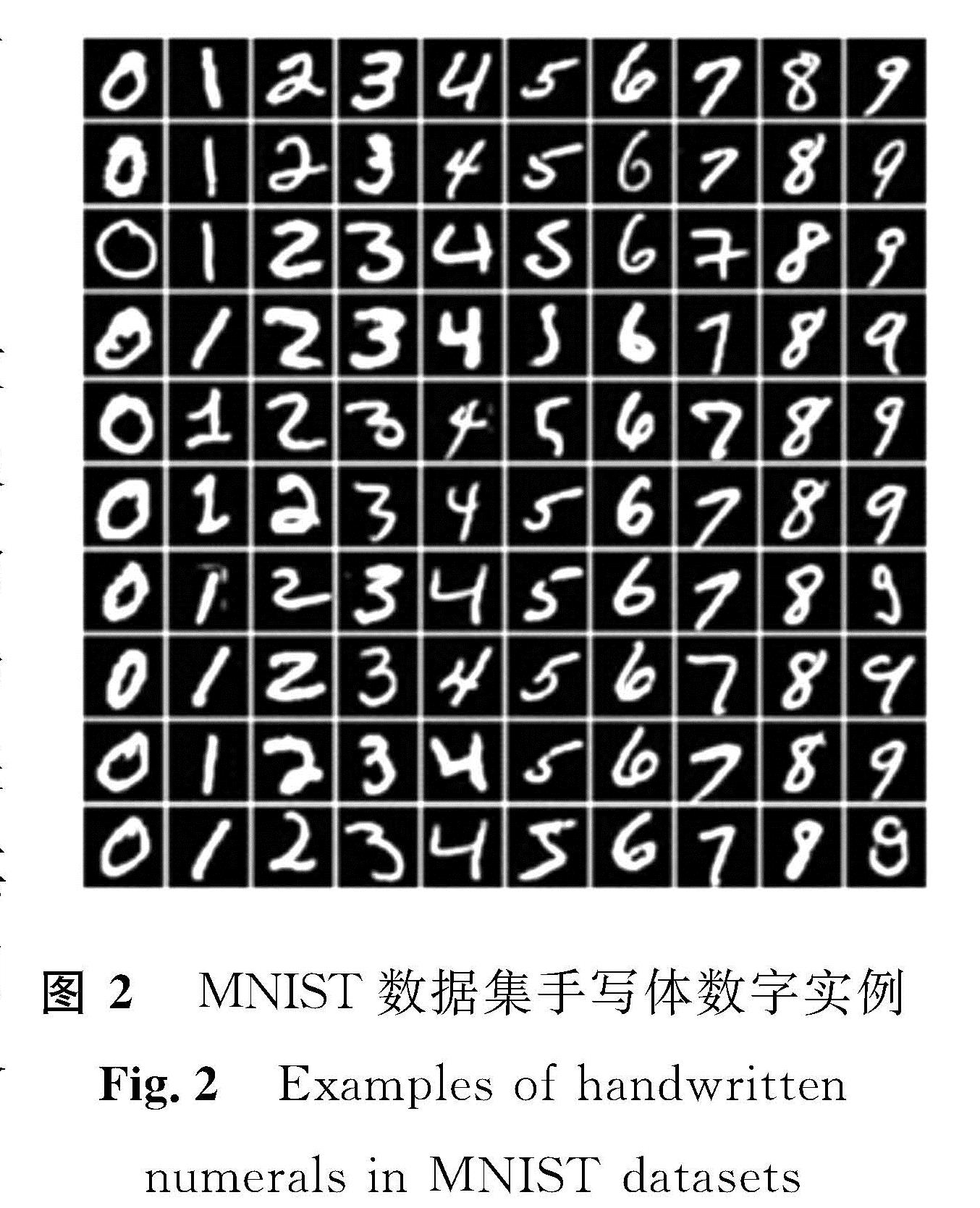
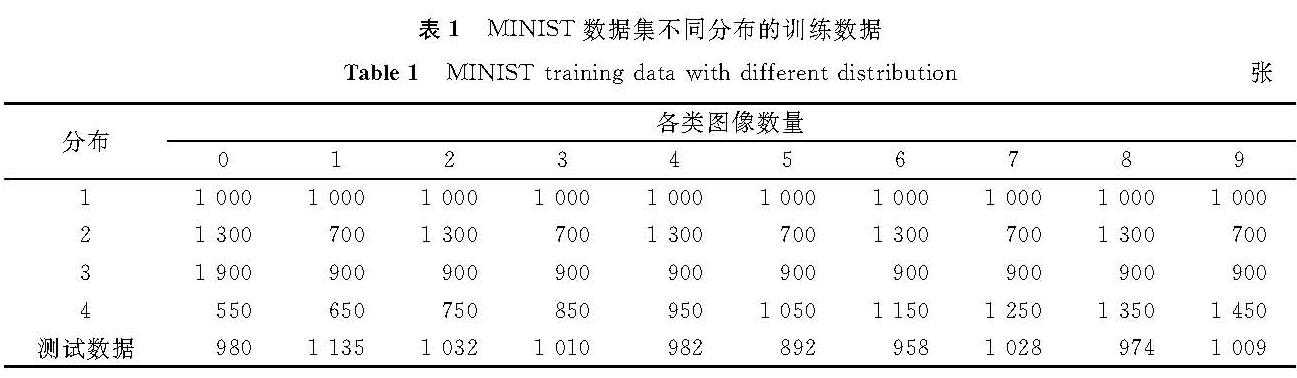
2.1 数据设置MNIST是一个被广泛应用于机器学习性能测试的手写体数字数据集,共包含10个类别,为0～9,图像均为灰度图像,由28×28个像素点构成,图2为MNIST数据集手写体数字实例。从中抽取数据构建4种各类数据比例不同的训练数据分布,各训练数据分布总数均为10 000张图片,其中分布1为数据均衡的情况,各类数据均为1 000张图片; 分布2为一类数据多于另一类数据; 分布3为某一类数据多于其余类数据; 分类4为各类数据量呈线性增长; 测试数据由MNIST划分,总数为10 000张图片,各类数据数量相近。MNIST数据集不同分布的训练数据见表1。
表1 MINIST数据集不同分布的训练数据
Table 1 MINIST training data with different distribution张
2.2 网络和训练参数设置
在数据集较为简单、数据量较少的情况下,模型过于复杂易导致过拟合,因此我们采用具有完整CNN结构但较为简单的一层卷积(卷积核大小为5×5,数量为20)、一层池化(最大池化,池化核大小为2×2)和两层全连接(神经元数分别为100、10)的CNN,最后一层全连接用Softmax输出结果。使用小批量随机梯度下降(mini-batch stochastic gradient descent,MSGD)算法进行训练,学习率为0.01,小批量大小为200,迭代次数为20 000,代价函数使用交叉熵代价函数,激活函数使用S函数、T函数和R函数分别进行试验。为了对比不同网络结构下的试验结果,在具有2个卷积池化层和2个全连接层的经典CNN结构LeNet-5上进行重复试验,激活函数使用R函数,代价函数为交叉熵代价函数,对网络参数做了一些调整,其余训练参数与上述的相同。本试验的硬件条件为:Win10 64位系统,3.30 GHz CPU,4 G内存等。在Python平台进行试验,并借助Theano库完成高性能计算。
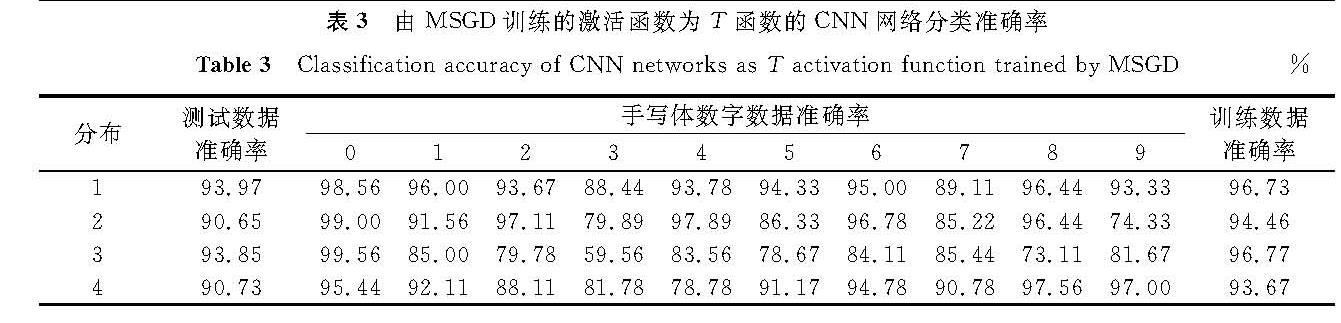
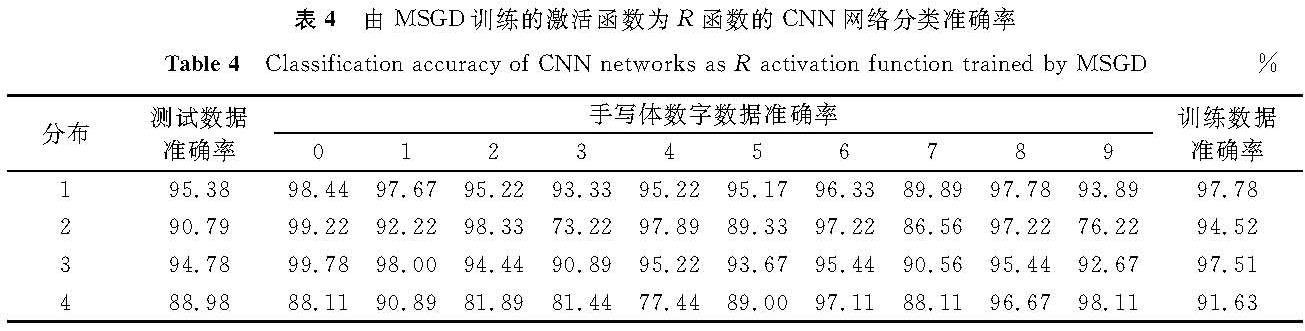
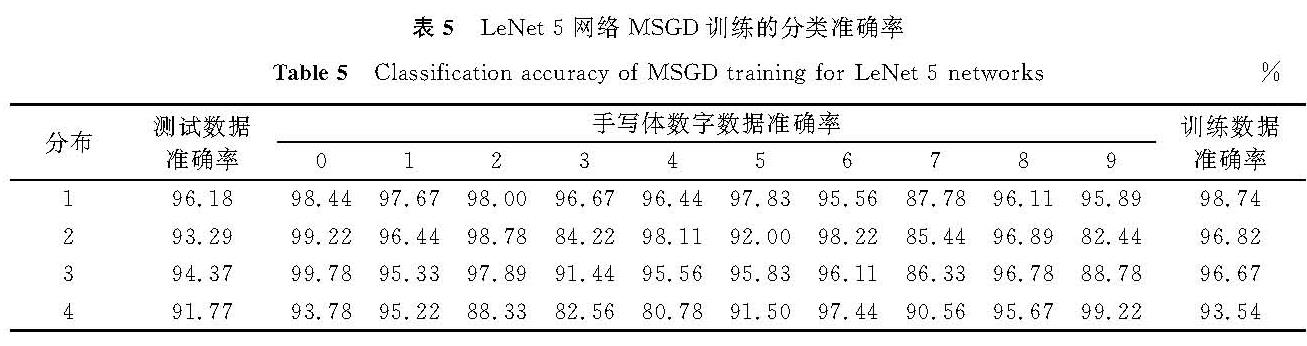
2.3 试验验证在不同训练数据和不同激活函数情况下由MSGD训练所得模型的CNN网络分类准确率见表2～4。表5是LeNet-5模型在不同训练数据下由MSGD训练所得模型的分类准确率。
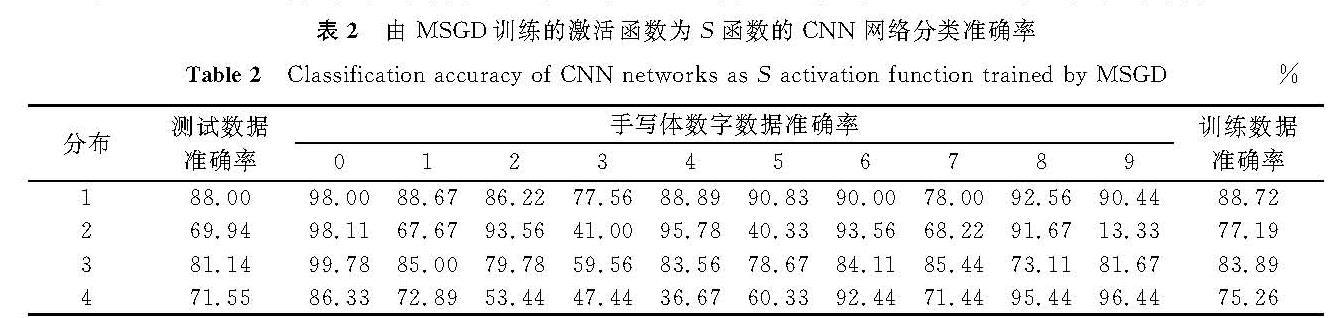
观察在S函数下各类别的分类准确率,发现大部分情况下训练数据越多的类别在测试阶段分类准确率越高,如表2分布2中偶数类,分布3中0类,分布4中8、9类。由表2可知,均衡数据(分布1)情况下训练得到的CNN模型分类准确率明显优于不均衡数据(分布2～4)情况下的分类准确率。而在相同的数据和网络结构情况下,采用不同的激活函数,发现也存在类似的情况。由表3和表4可知,在相同激活函数下,均衡数据(分布1)训练得到的CNN模型测试准确率要高于不均衡数据(分布2～4)。由表5可知,不均衡训练数据同样会对不同的CNN模型造成影响。虽然LeNet-5模型在不同数据分布情况下得到的模型分类准确率较高,可以在一定程度上降低不均衡数据带来的不良影响,但是均衡数据(分布1)情况下得到的CNN模型分类准确率还是明显优于不均衡数据(分布2～4)情况下的分类准确率。
表2 由MSGD训练的激活函数为S函数的CNN网络分类准确率
Table 2 Classification accuracy of CNN networks as S activation function trained by MSGD%
表3 由MSGD训练的激活函数为T函数的CNN网络分类准确率
Table 3 Classification accuracy of CNN networks as T activation function trained by MSGD%
表4 由MSGD训练的激活函数为R函数的CNN网络分类准确率
Table 4 Classification accuracy of CNN networks as R activation function trained by MSGD%
表5 LeNet-5网络MSGD训练的分类准确率
Table 5 Classification accuracy of MSGD training for LeNet-5 networks%
3 EMSGD的提出与试验结果
为解决前述不均衡训练数据对CNN的不良影响,我们提出改进算法EMSGD。与随机梯度下降算法的对比试验结果表明,我们提出的改进算法是有效的。
3.1 算法思想与实现与随机梯度下降算法不同的是,我们的改进算法从原来随机抽取训练数据组成小批量,改进为从每类数据抽取相同数量的样本组成小批量,使得小批量内部保持类别均衡。改进算法的目的是要保证小批量内的数据均衡,因此对少数类,我们采取过抽样,而对多数类,则采取欠抽样。该算法的优点是即使对少数类采取过抽样,只需满足小批量内的均衡即可,不需要像传统的过抽样技术那样满足整个训练数据的均衡,因此少数类的重复样本会比较少。另外,对多数类而言,它只是在小批量内进行了欠采样。由于训练过程是由多个时期(epoch)组成,最终所有的多数类样本都会被用于训练,所以也不存在因欠采样而导致信息丢失的问题。通过保持小批量内的数据均衡,改进算法不仅可以消除数据不均衡带来的不良影响,还可以优化梯度下降的方向,使模型训练收敛更快。
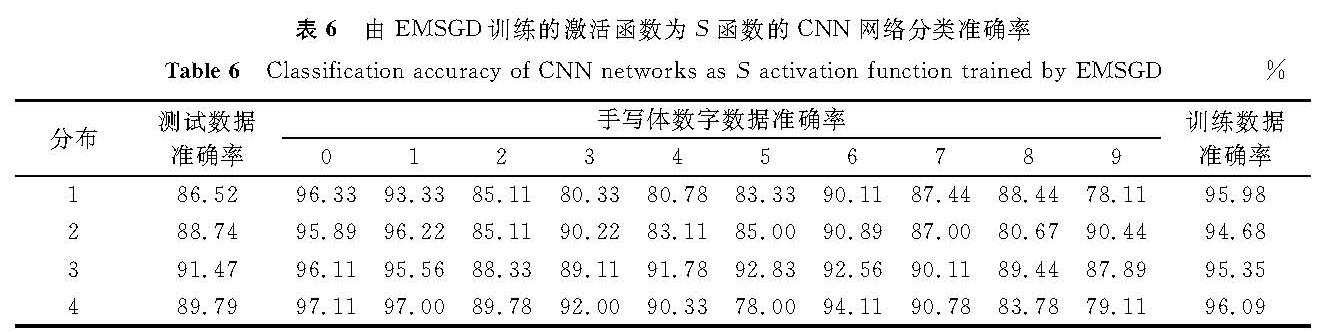
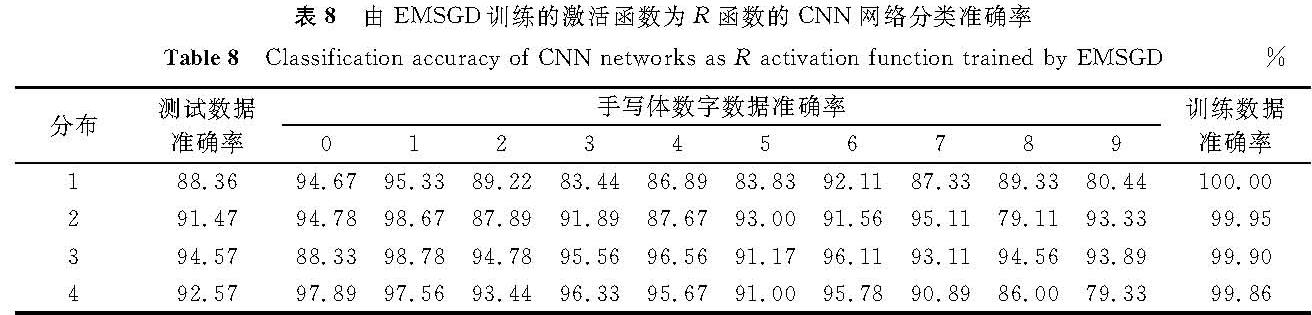
3.2 试验评估EMSGD的性能评估采用与前述试验相同的CNN结构和数据,激活函数分别采用S函数、T函数和R函数,试验结果见表6～8,在LeNet-5网络的试验结果见表9。在激活函数为S函数的情况下,与传统的随机梯度下降算法相比,改进算法的准确率更高。由表2可知,数据分布2在随机梯度下降算法下测试数据准确率只有69.94%,而表6显示改进算法的测试数据准确率可达88.74%,提高近20%。在不同的数据分布下,改进算法都可有效提高少数类的准确率,如分布2中1类数据的准确率从67.67%(表2)提高到96.22%(表6)。
在激活函数为T函数和R函数的情况下,尽管传统的随机梯度下降算法测试数据准确率可以达到90%左右,但在某些少数类上准确率仍然较低。如表3中分布3的3类数据的准确率只有59.56%,而同样情况下的改进算法使少数类的准确率均可达到80%左右,这说明改进算法可有效提高CNN对少数类的分类准确率。
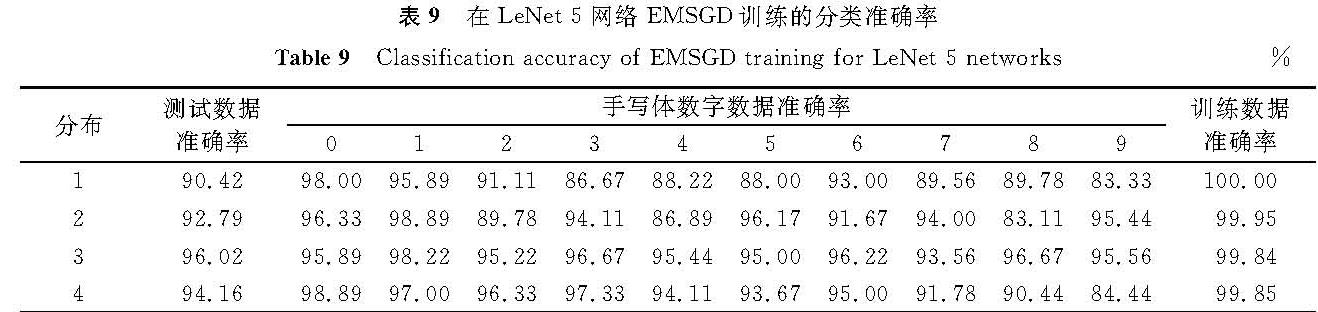
对比表9和表5可知改进算法在LeNet-5同样有效,在数据不均衡的情况下模型准确率有所提升,比如分布4的测试数据准确率由91.77%提高至94.16%,并且可以有效提高少数类的分类准确率,比如分布3的9类由88.78%提高至95.56%。
表6 由EMSGD训练的激活函数为S函数的CNN网络分类准确率
Table 6 Classification accuracy of CNN networks as S activation function trained by EMSGD%
表7 由EMSGD训练的激活函数为T函数的CNN网络分类准确率
Table 7 Classification accuracy of CNN networks as T activation function trained by EMSGD%
表8 由EMSGD训练的激活函数为R函数的CNN网络分类准确率
Table 8 Classification accuracy of CNN networks as R activation function trained by EMSGD%
表9 在LeNet-5网络EMSGD训练的分类准确率
Table 9 Classification accuracy of EMSGD training for LeNet-5 networks%
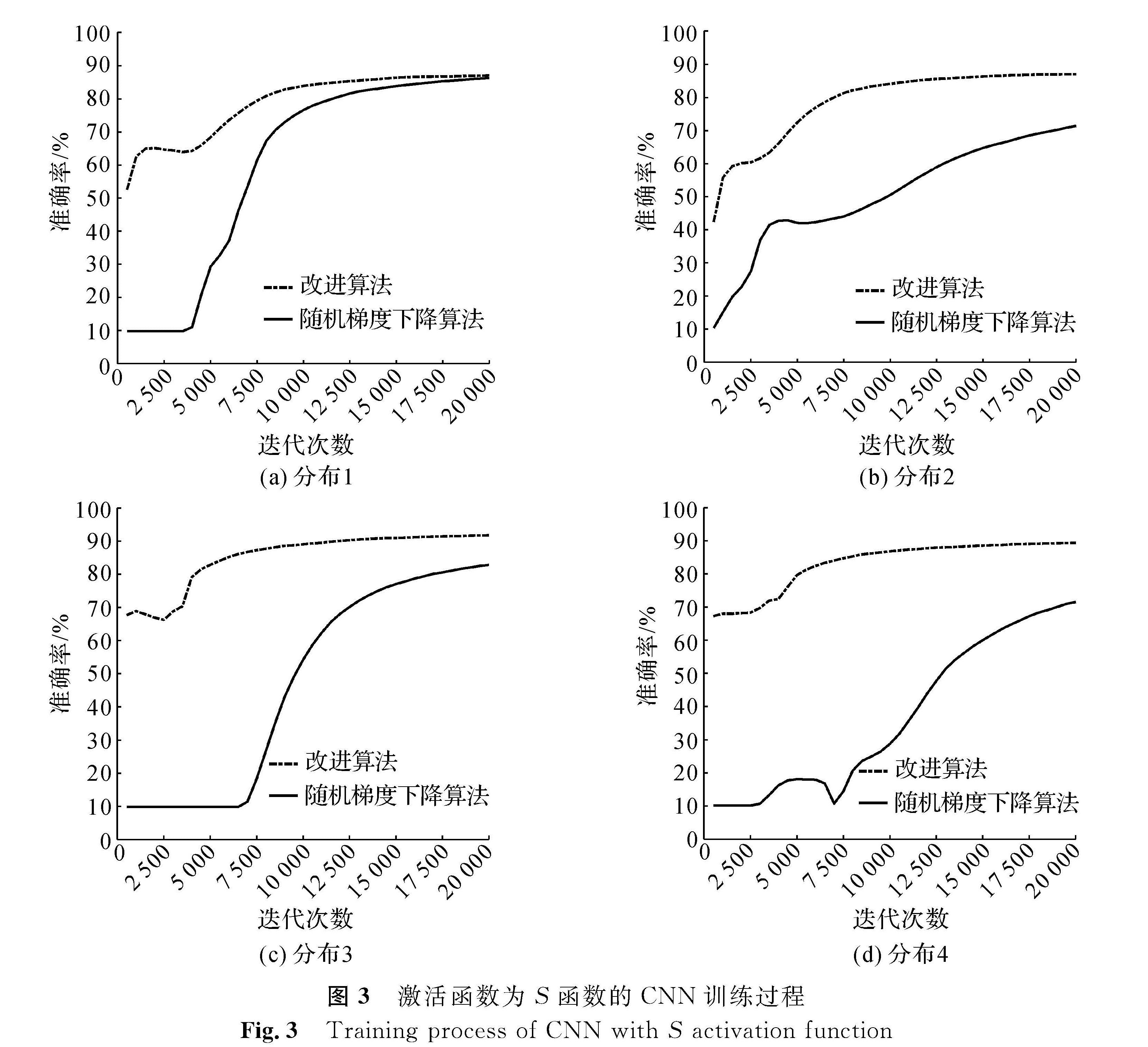
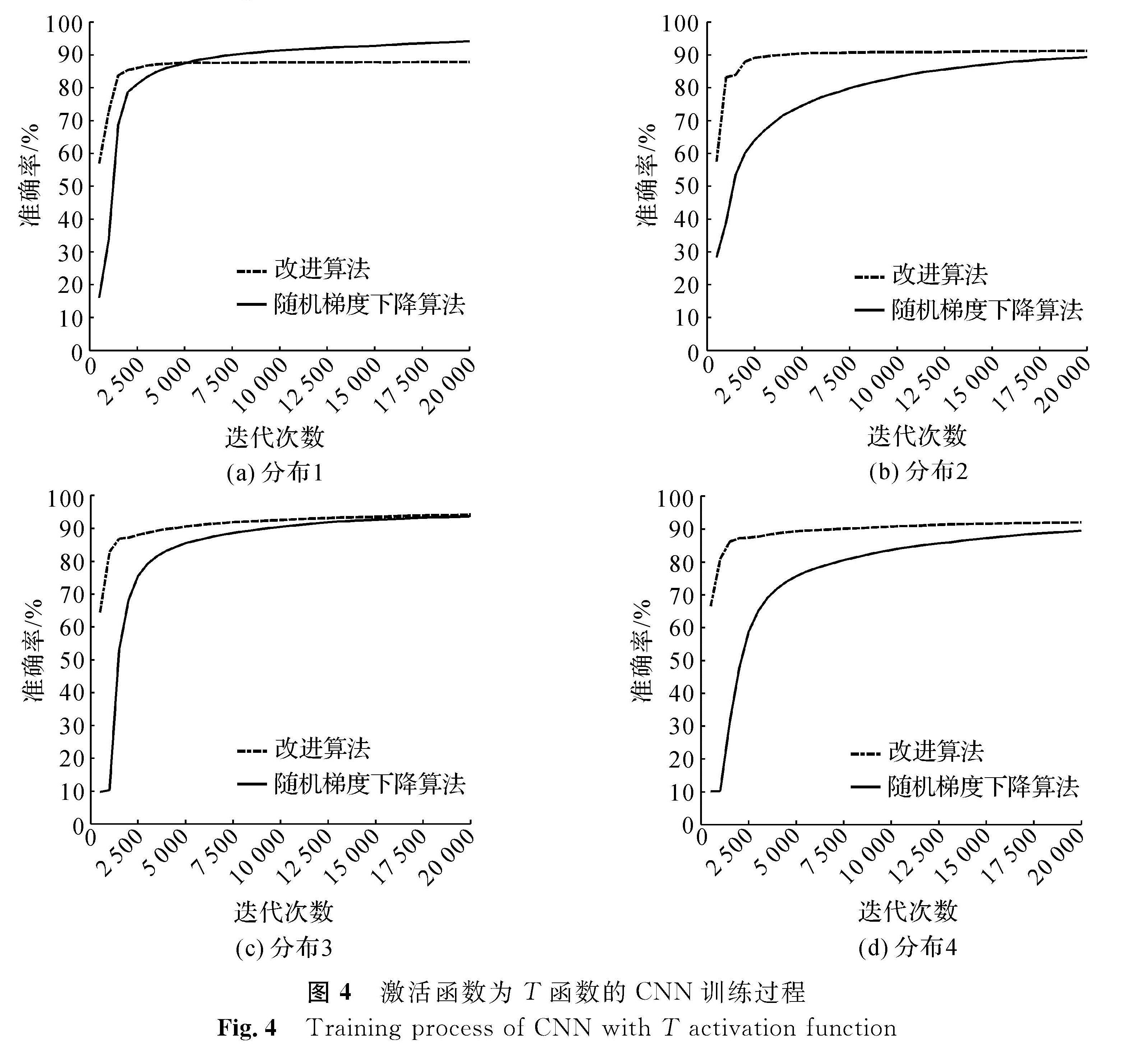
在数据不均衡的情况下,改进算法比随机梯度下降算法可以更快地收敛。图3～5分别为激活函数为S函数、T函数、R函数时,CNN在4种不同训练数据分布情况下的训练过程。
由图3可知,针对4种不同分布的数据,在激活函数为S函数的情况下,使用改进算法在前期迭代中会更快地达到一个较高的准确率。如图3(a)所示,改进算法在第7 500次迭代时,准确率就达到了80%,而传统的随机梯度下降算法前期准确率提高较慢,在7 500次迭代时准确率只达到50%。训练完成后,改进算法训练得到的CNN测试准确率更高,在数据不均衡的情况下(如图3(b)、(c)、(d))表现得更为明显。
图4、图5是模型在激活函数为T函数和R函数时在4种不同数据分布情况下的训练过程。与S函数的情况相似,改进算法比随机梯度下降算法在不均衡数据集上的收敛速度更快,且准确率更高。但与图3不同的是,图4(a)和图5(a)中,使用随机梯度下降算法达到的准确率略高于使用改进算法。由对应的表7和表8可以发现,在分布1的情况下,改进算法的训练数据准确率比随机梯度下降算法要高,而测试数据准确率反而降低,由此可推断改进算法可能在数据均衡的情况下易发生过拟合,更适合应用于数据不均衡情况。
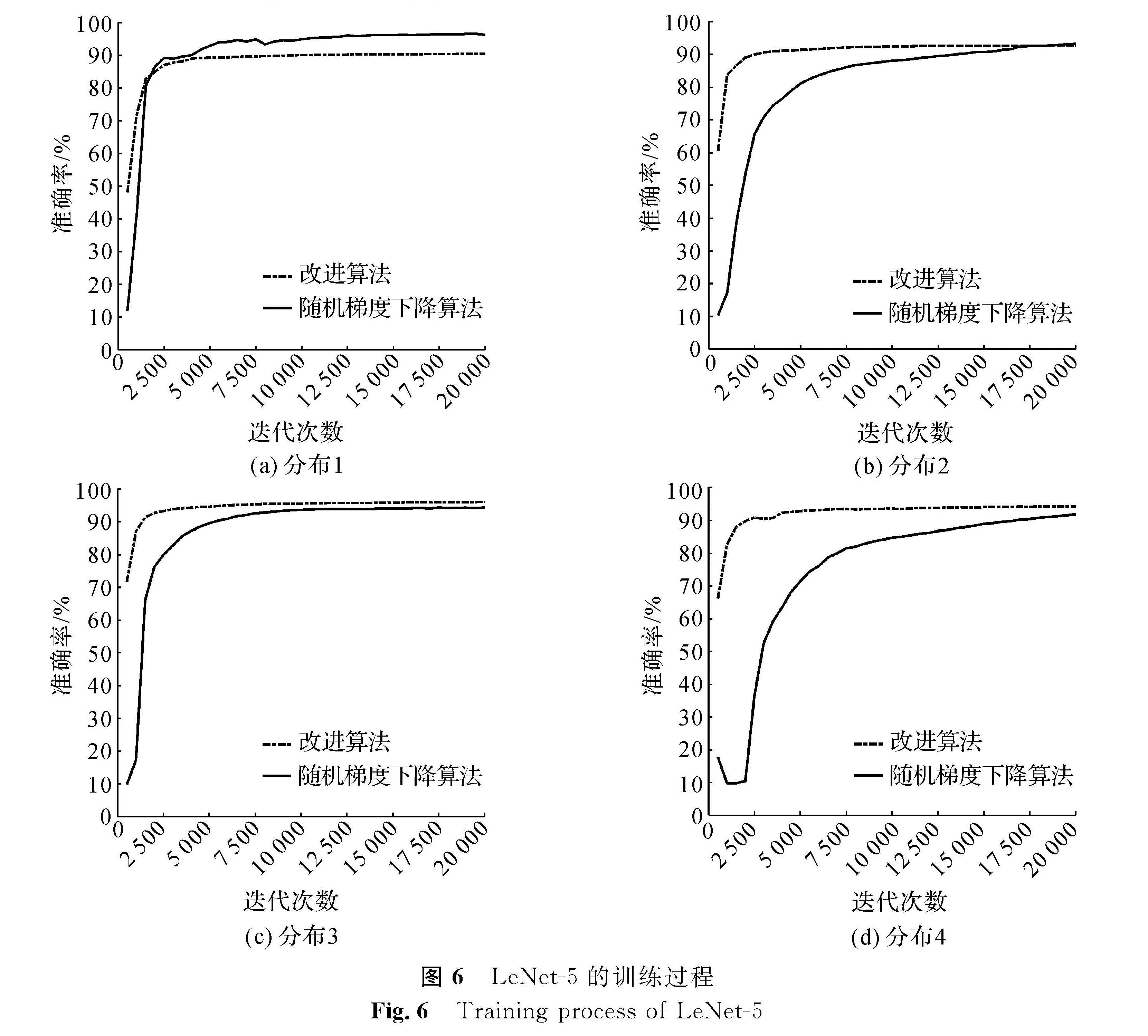
图6是LeNet-5在4种不同数据分布情况下的训练过程。与图5相似,改进算法比随机梯度下降算法在不均衡数据上的收敛速度更快,且准确率更高,试验证明了我们提出的改进算法在不同的网络结构下均是有效的。但由于LeNet-5模型更复杂,易发生过拟合,因此在分布1和分布2情况下的模型最终的性能没有太大的提升,反而略低于随机梯度下降算法训练得到的模型。
图3 激活函数为S函数的CNN训练过程
Fig.3 Training process of CNN with S activation function
图4 激活函数为T函数的CNN训练过程
Fig.4 Training process of CNN with T activation function
图5 激活函数为R函数的CNN训练过程
Fig.5 Training process of CNN with R activation function
图6 LeNet-5的训练过程
Fig.6 Training process of LeNet-5
4 结 语
本文讨论了不均衡数据对CNN训练造成的不良影响。通过试验我们发现,在多种数据不均衡情况下CNN训练过程中的不良特征,尤其是少数类的准确率较低。试验进一步发现在不同激活函数的情况下都存在这种不良特征,对此我们提出传统的随机梯度下降算法的改进算法——均衡小批量随机梯度下降算法,在每次迭代计算梯度时,保持小批量内数据的类别均衡,克服数据不均衡带来的负面影响。与随机梯度下降算法相比,试验结果表明改进算法在多种激活函数和不同网络结构的情况下,均能提高CNN的正确率,并且收敛速度更快,适合在数据不均衡的情况下使用。本文提出的改进方法可以进一步完善,主要方向为如何防止可能会出现的过拟合问题,并可以与AdaDelta、Adam等优化方法相结合。
- [1] HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE,2016:770.
- [2] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Advances in Neural Information Processing Systems. Lake Tahoe: NIPS,2012:1097.
- [3] HINTON G, DENG L, YU D, et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups[J].IEEE Signal Processing Magazine,2012,29(6):82.
- [4] XIONG W, DROPPO J, HUANG X, et al. Toward human parity in conversational speech recognition[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing,2017,25(12):2410.
- [5] SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[C]//Advances in Neural Information Processing Systems. Montreal: NIPS,2014:3104.
- [6] HE D, XIA Y C, QIN T, et al. Dual learning for machine translation[C]//Advances in Neural Information Processing Systems. Baecelona: NIPS,2016:820.
- [7] BHATTACHARYA S, RAJAN V, SHRIVASTAVA H. ICU mortality prediction: a classification algorithm for imbalanced datasets[C]//Proceeding of the Thirty-First AAAI Conference on Artificial Intelligence. San Francisco: AAAI,2017:1288.
- [8] ZAKARYAZAD A, DUMAN E. A profit-driven artificial neural network(ANN)with applications to fraud detection and direct marketing[J].Neurocomputing,2016,175:121.
- [9] WANG S, YAO X. Using class imbalance learning for software defect prediction[J].IEEE Transactions on Reliability,2013,62(2):434.
- [10] DUAN L X, XIE M Y, BAI T B, et al. A new support vector data description method for machinery fault diagnosis with unbalanced datasets[J].Expert Systems with Applications,2016,64:239.
- [11] KHAN S H, HAYAT M, BENNAMOUN M, et al. Cost-sensitive learning of deep feature representations from imbalanced data[J].IEEE Transactions on Neural Networks and Learning Systems,2015,29(8):3573.
- [12] KRAWCZYK B. Learning from imbalanced data: open challenges and future directions[J].Progress in Artificial Intelligence,2016,5(4):221.
- [13] GUO H X, LI Y J, JENNIFER S, et al. Learning from class-imbalanced data: review of methods and applications[J].Expert Systems with Applications,2017,73:220.
- [14] HE H B, GARCIA E A. Learning from imbalanced data[J].IEEE Transactions on Knowledge and Data Engineering,2009,21(9):1263.
- [15] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research,2002,16(1):321.
- [16] DRUMMOND C, HOLTE R C. C4.5, class imbalance, and cost sensitivity: why under-sampling beats over-sampling[C]//Workshop on Learning from Imbalanced Datasets II. Washington DC: Citeseer,2003.
- [17] ELKAN C. The foundations of cost-sensitive learning[C]//International Joint Conference on Artificial Intelligence. Washington DC: Morgan Kaufmann,2001.
- [18] MAZUROWSKI M A, HABAS P A, ZURADA J M, et al. Training neural network classifiers for medical decision making: the effects of imbalanced datasets on classification performance[J].Neural Networks,2008,21(2/3):427.
- [19] JACCARD N, ROGERS T W, MORTON E J, et al. Detection of concealed cars in complex cargo X-ray imagery using deep learning[J].Journal of X-ray Science and Technology,2017,25(3):323.
- [20] JANOWCZYK A, MADABHUSHI A. Deep learning for digital pathology image analysis: a comprehensive tutorial with selected use cases[J].Journal of Pathology Informatics,2016,7(1):29.
- [21] CHUNG Y A, LIN H T, YANG S W. Cost-aware pre-training for multiclass cost-sensitive deep learning[C]//Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence. Melbourne: AAAI,2016:1411.
- [22] KHAN S H, HAYAT M, BENNAMOUN M, et al. Cost-sensitive learning of deep feature representations from imbalanced data[J].IEEE Transactions on Neural Networks and Learning Systems,2015,29(8):3573.
- [23] HAVAEI M, DAVY A, WARDE-FARLEY D, et al. Brain tumor segmentation with deep neural networks[J].Medical Image Analysis,2017,35:18.
- [24] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J].Proceedings of the IEEE,1998,86(11):2278