汽车动力总成悬置系统具有减少并控制汽车发动机振动传递、支撑发动机和定位发动机相对于车架位置的功能,因此要求悬置具有一定的刚度、弹性,同时具备高阻尼的特性。而橡胶材料恰恰可以很好地满足这一要求,因此橡胶悬置被广泛地应用在整车悬置系统中。橡胶悬置由橡胶主体和金属支架等零件组成,相较于液压悬置,拥有结构紧凑、性价比高、便于维护及使用寿命较长等优点^[1]。而橡胶悬置作为一种车用隔振元件,对隔离振动、降低噪声及改善整车NVH(noise、vibration、harshness,噪声、振动、声振粗糙度)性能有着极为重要的作用。

橡胶悬置静态特性可以反映出在不同荷载下悬置静刚度的变化情况,悬置静刚度作为悬置各项特性研究的基础,可为优化悬置系统的整体性能提供可靠依据。合理的悬置静刚度还可以避免动力总成过度位移而引起的发动机与车架相碰撞的情况^[2]。

橡胶悬置的静刚度通常是在特定的试验仪器上测试获得的,以往通过对悬置逐一测量获取静刚度的方法过程繁琐,耗费大量的人力物力。随着有限元技术的发展,目前橡胶悬置刚度的预测与计算主要通过有限元分析软件来实现,如文献[3-4]在已有本构模型参数的基础上,通过对橡胶悬置进行有限元分析来获得其静刚度值,并与实际值对比来验证各模型计算结果的准确性; 文献[5-6]结合给定的本构模型参数与有限元分析方法来研究橡胶悬置结构对其静刚度的影响; 文献[7-8]同样在已有本构模型参数的基础上,利用仿真软件来计算橡胶悬置的静刚度及应力-应变变化情况以指导悬置设计。不难发现,借助有限元分析可以高效地对橡胶悬置类产品开展各项研究。然而,上述研究均是在本构模型参数已知的情况下展开的,对使用新型胶料或混合胶料的橡胶悬置而言,上述的方法就有所欠缺。随着对橡胶类产品研究的不断深入,人们已经找到多种本构模型参数的获取方法,文献[9-11]通过橡胶材料硬度与力学参数的经验公式来获得Mooney-Rivlin模型的本构模型参数,此类方法操作简便,但获取的参数精度不高,会导致仿真结果误差较大。除此之外,文献[12-15]还提供了一种通过对橡胶材料进行基础力学试验,如单轴拉伸试验、等双轴拉伸试验和平面拉伸试验来获得应力-应变曲线,再通过曲线拟合的方法来获取本构模型参数的方法。通过该方法获取的参数有较高的准确性,也是目前使用最为广泛的本构模型参数的获取方法,但该方法对试验设备有较高的要求,试验成本相对较高。基于上述研究,笔者提出一种采用单轴拉伸试验获取橡胶本构模型参数,以此作为有限元仿真试验基础,并通过有限元分析软件获取衬套类橡胶悬置静刚度的方法。

对橡胶等超弹性材料而言,一般假设其外部荷载所做的功全部存储于弹性体内,通常将反映其变形梯度与应变势能函数关系的模型称为本构模型。对橡胶本构模型展开研究是非常有必要的,它的本构关系是研究橡胶力学性能的基础。橡胶材料的本构理论研究可以分为统计热力学法和唯象学法。橡胶作为一种各向同性、近乎不可压缩的超弹性材料,通常用应变能密度函数来表征其物理属性^[16]。人们通过对橡胶应变能密度函数的多年研究,推导出了多种形式的超弹性材料本构模型,其中应用较广泛的有Mooney-Rivlin模型、Yeoh模型、Ogden模型、Arruda-Boyce模型和Van Der waals模型等^[17]。这些模型分别有不同的表达形式,表达式中的自变量为应变不变量和主伸长率,适用的场合和条件也不尽相同,合理地选用模型类型可以保证对橡胶材料力学特性分析的精确性。

Abaqus等通用的非线性有限元软件在计算橡胶材料力学性能时大多采用Mooney-Rivlin模型,该模型的拟合效果较好,大多数橡胶材料的力学性能都可以通过该模型来进行预测分析。但是该模型同样存在缺陷,仅能对中小应变条件下的橡胶力学性能做到精确模拟,而无法模拟在大应变条件下的力学性能。对所选衬套类橡胶悬置的静刚度有限元计算在小应变的范围内,因此采用Mooney-Rivlin模型,该模型的表达式为

W=C₁₀(I₁-3)+C₀₁(I₂-3)+((J-1)²)/(D₁)。(1)

式(1)中:W为单位体积的应变势能; C₁₀、C₀₁为Mooney-Rivlin模型参数; I₁、I₂分别为一阶、二阶的应变不变量; J为弹性体积比,由于橡胶材料有着极高的弹性体积模量,故定义J=1; D₁为压缩特性。因此可以将式(1)简化为

W=C₁₀(I₁-3)+C₀₁(I₂-3)。

而橡胶材料的初始剪切模量G和体积模量K₀分别为

G=2(C₁₀+C₀₁); K₀=2/(D₁)。

根据Mooney-Rivlin模型,单轴拉伸时橡胶材料的应力-应变关系式为

σ=2C₁₀[1+ε-1/((1+ε)²)]+2C₀₁[1-1/((1+ε)³)]。(2)

式(2)中:σ为Mooney-Rivlin模型下的应力; ε为拉伸应变。

基础力学试验包括对材料的单轴拉伸、等双轴拉伸及平面拉伸等多种应变的试验,在获得相应的应力-应变试验数值曲线后可采用最小二乘法进行曲线拟合来求得模型参数^[18-19]。单轴拉伸试验作为构建超弹性模型试验中的基础试验,为了获得最纯的拉伸应变状态,一般都选用在拉伸方向的长度远大于宽度和厚度的试件。而等双轴拉伸试验在应变状态上等效于单轴压缩试验,由于在实际操作过程中难以实现单轴压缩,因此通过等双轴拉伸试验来获取纯压缩情况下的应力-应变关系。平面拉伸实质上是一种剪切应变的状态,要求试件有较大的长宽比。后两种试验对设备有较高的要求。

本次单轴拉伸试验选用哑铃状橡胶试件,如图1所示。试件胶料与所选定橡胶悬置胶料一致,不同于被人们研究较多的N45、N50和N55橡胶胶料,此次单轴拉伸试验所用胶料的配方成分较新,编号为N48-8。

哑铃状试件的宽为6.1 mm,厚为2.18 mm,符合标准试验尺寸。试件根据要求夹在拉伸机的上下两个夹片上,将拉伸机设置好参数后进行橡胶单轴拉伸试验,如图2所示。按照GB/T 528—2009 《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》^[20],其加载速度在(500±50)mm/min范围内,试验环境温度处在(23±5)℃范围内。本次试验加载速度为500 mm/min,环境温度为23 ℃,因此符合测定要求。

图1 哑铃状橡胶试件
Fig.1 Specimens of dumbbell-type rubber

图2 橡胶单轴拉伸试验
Fig.2 Rubber uniaxial tensile test

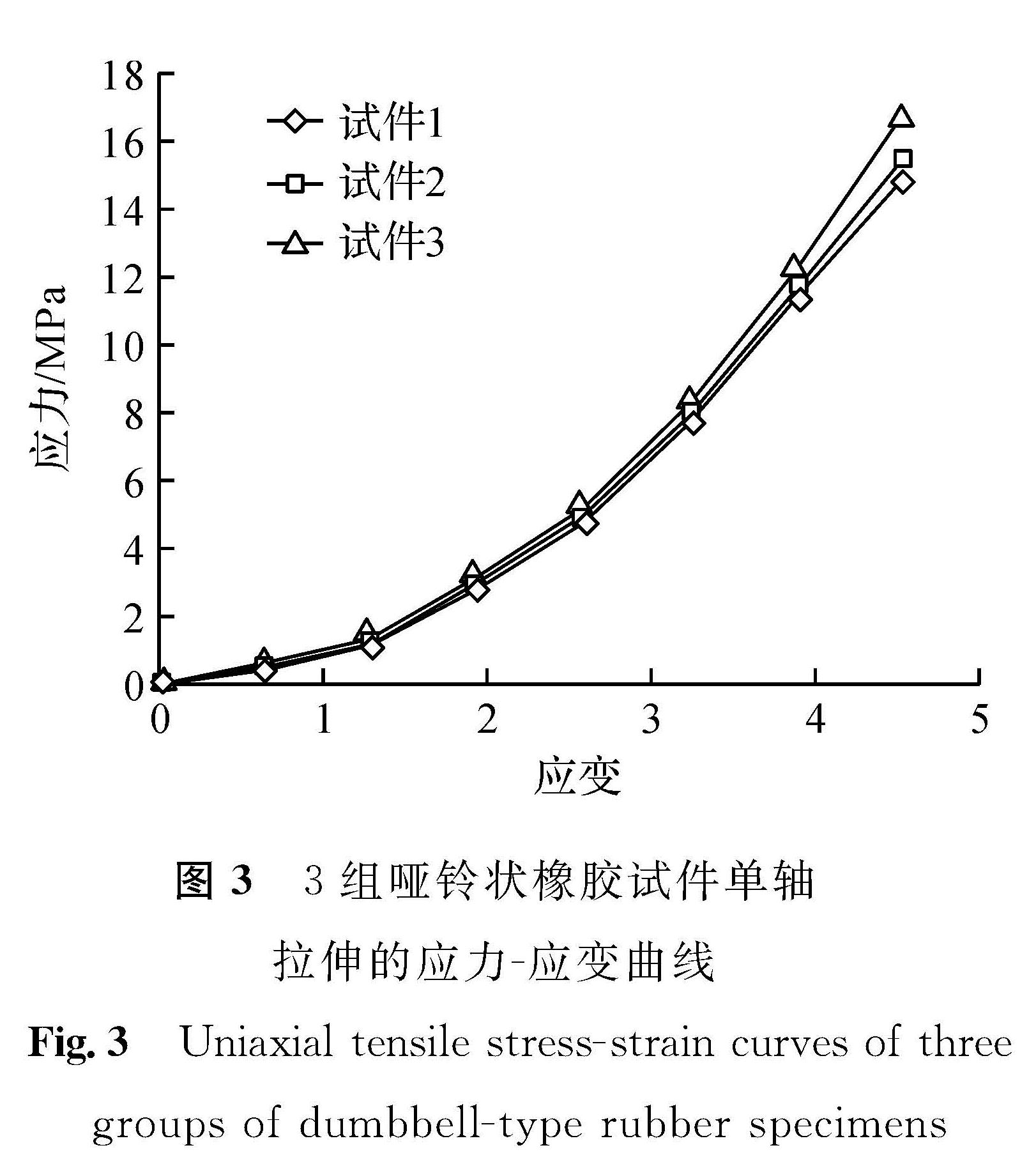
图3 3组哑铃状橡胶试件单轴拉伸的应力-应变曲线
Fig.3 Uniaxial tensile stress-strain curves of three groups of dumbbell-type rubber specimens

试验完成后获得3组哑铃状橡胶试件单轴拉伸的应力-应变数据,将数据整理后在excel中绘制成曲线,如图3所示。从图3可以看出,3组哑铃状橡胶试件应力-应变数据较为接近,体现了橡胶材料力学性能较高的一致性; 同时也能看出在小应变阶段内橡胶应力-应变曲线更接近于直线。该小应变范围内的数据是后续求取Mooney-Rivlin模型参数的基础。

在获得橡胶材料单轴拉伸应力-应变曲线后,需将试验数据导入Abaqus软件中进行曲线拟合来获得橡胶Mooney-Rivlin模型参数值。曲线拟合的依据为式(2),由于Mooney-Rivlin模型适用于小应变范围,因此选取小应变范围内的几组应力-应变值导入软件即可完成曲线拟合。具体过程如下:先在Abaqus软件中创建一种材料属性,在“力学”栏中选择

图4 橡胶材料单轴拉伸的应力-应变拟合曲线
Fig.4 Uniaxial tensile stress-strain fitting curve of rubber material derived by Abaqus

“超弹性”项; 在“应变势能”栏中选取“Mooney-Rivlin模型”; 在“等轴试验数据”的表格中填入试件小应变范围内的几组数据; 随后对创建的材料进行评估,在“评估”栏中仅选择“单轴拉伸”选项,点击“确定”开始进行数据拟合。

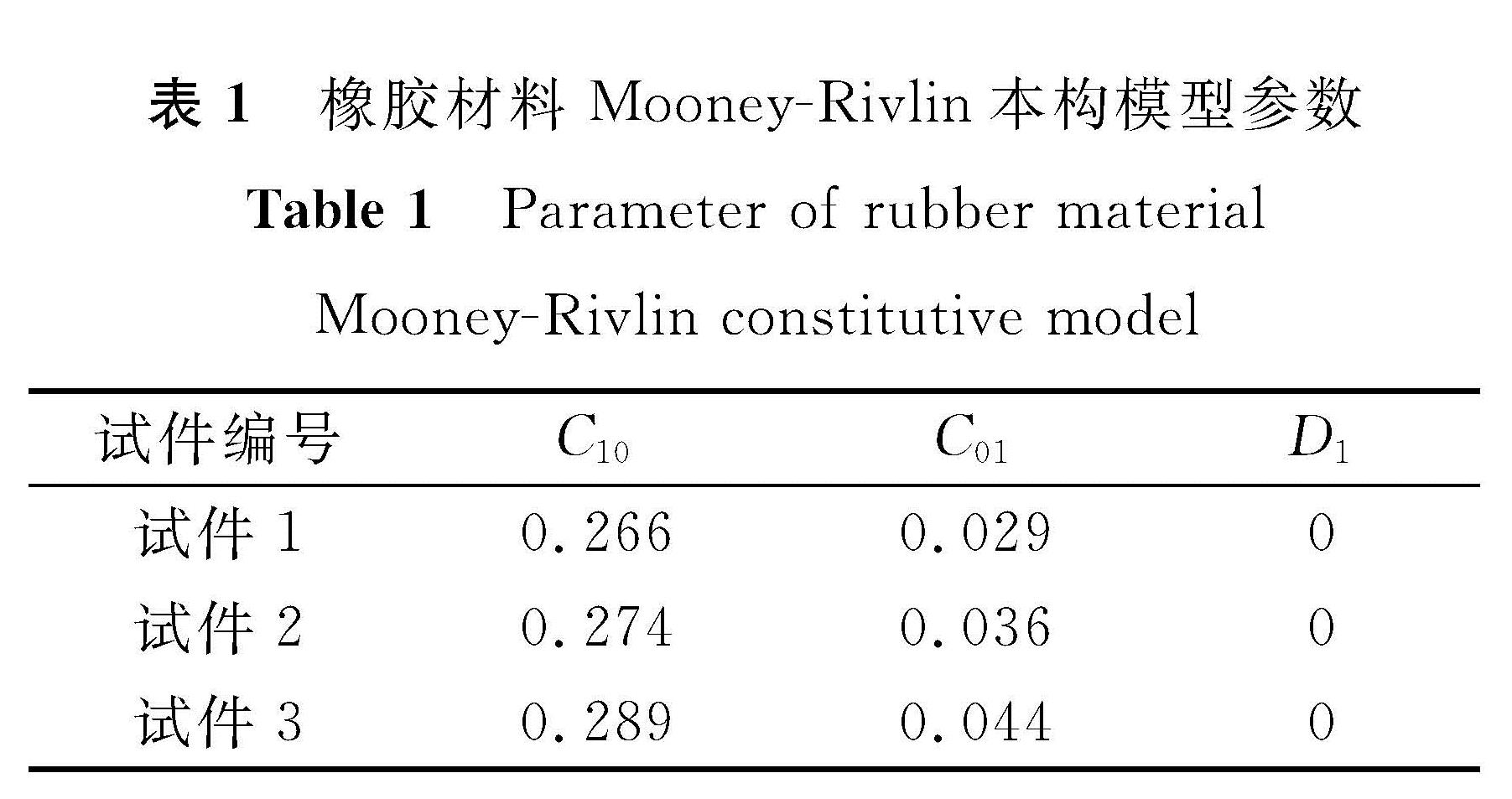
数据拟合完成后,可以从软件界面上获得橡胶材料的应力-应变拟合曲线和橡胶Mooney-Rivlin本构模型参数值,橡胶材料单轴拉伸的应力-应变拟合曲线如图4所示,Mooney-Rivlin本构模型参数见表1。

表1 橡胶材料Mooney-Rivlin本构模型参数
Table 1 Parameter of rubber material Mooney-Rivlin constitutive model

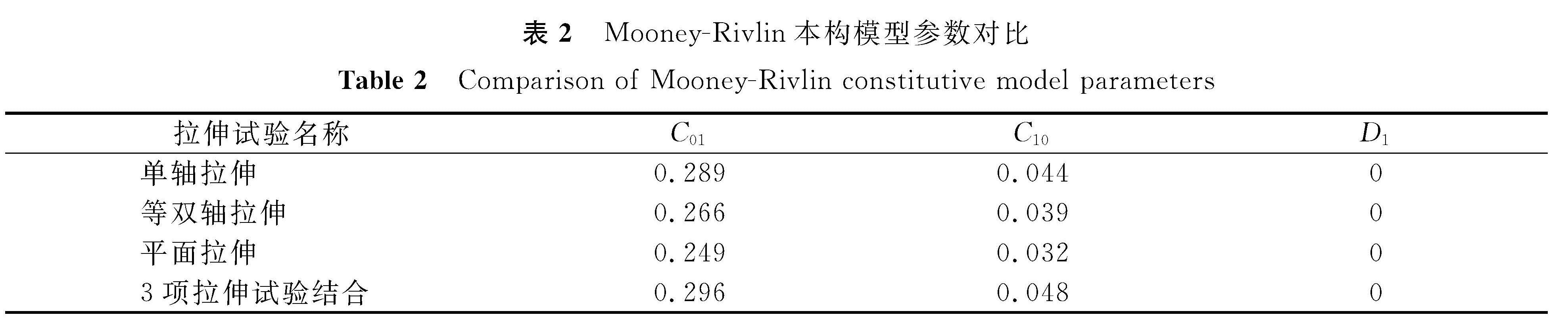
在获得了单轴拉伸试验所对应的Mooney-Rivlin本构模型参数的情况下,采用同样的方法获取等双轴拉伸、平面拉伸试验下的N48-8材料应力-应变曲线,并且在Abaqus软件中对等双轴拉伸试验曲线数据、平面拉伸试验曲线数据,及将单轴拉伸、等双轴拉伸、平面拉伸3组拉伸试验结合的曲线数据进行拟合,获得各自对应的Mooney-Rivlin本构模型参数,各组拉伸试验所得到的Mooney-Rivlin本构模型参数对比见表2。将3项拉伸试验结合的曲线拟合得到的模型参数作为标准值,从表2可以看出,通过单轴拉伸试验所获得的Mooney-Rivlin本构模型参数最接近标准值,因此选用单轴拉伸试验中试件3的参数值作为后续仿真试验的输入值。

表2 Mooney-Rivlin本构模型参数对比
Table 2 Comparison of Mooney-Rivlin constitutive model parameters

本研究所选用的衬套类橡胶悬置实物如图5所示,其结构形式是悬置中较为常见的八字形,即该悬置左右主簧之间的夹角范围在60°到150°之间。通过该类型的布置方式可以使得橡胶悬置在受到Z向荷载时主要承受的是拉压荷载,从而有效地提高悬置的疲劳寿命,因此该结构的悬置受到广泛的应用。

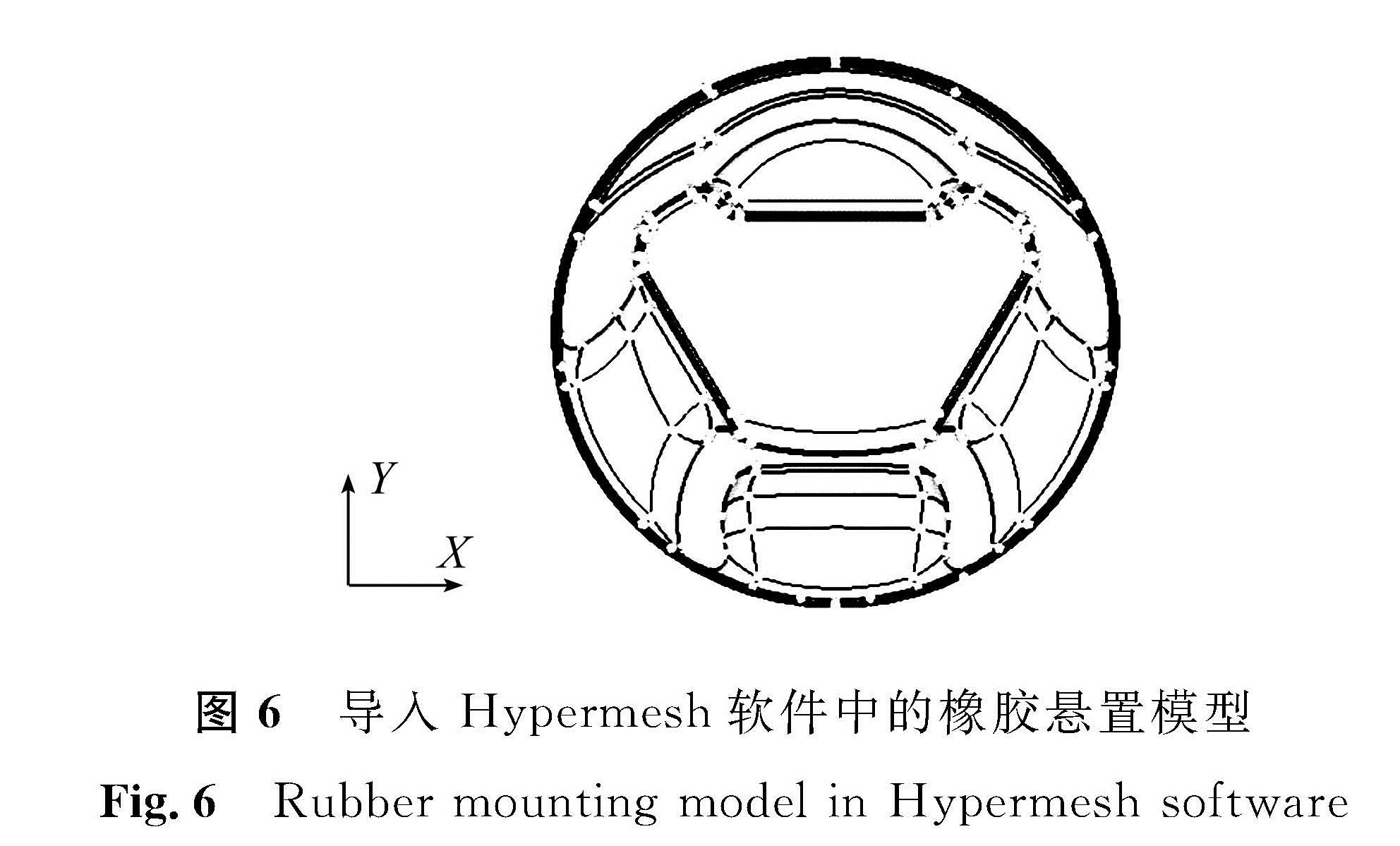
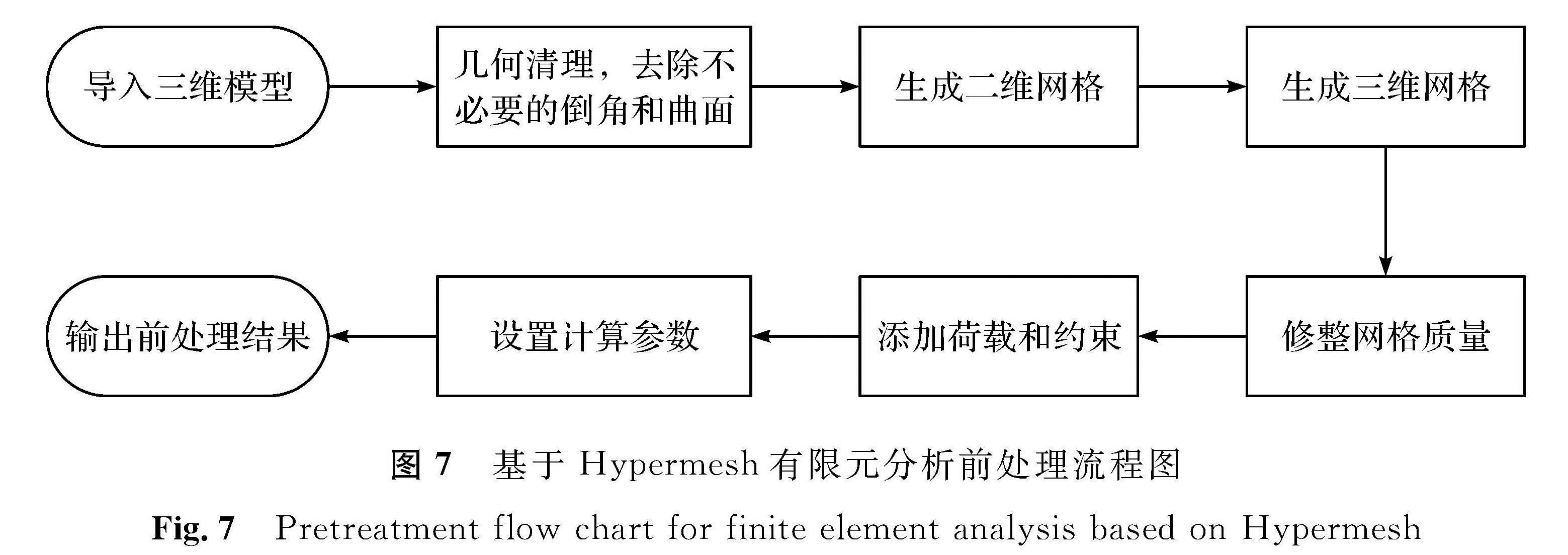
对于该款衬套类的橡胶悬置,通过Unigraphics NX软件完成三维模型的建立后,将其导入Hypermesh软件中进行有限元分析前处理。之后,规定橡胶悬置的参考坐标系,便于统一与后续的数据整理,导入的模型和坐标系如图6所示。X向和Y向已在图6中标出,Z向为悬置高度方向。基于Hypermesh有限元分析前处理流程图如图7所示。

图5 衬套类橡胶悬置实物
Fig.5 Bushing rubber mount

图6 导入Hypermesh软件中的橡胶悬置模型
Fig.6 Rubber mounting model in Hypermesh software

图7 基于Hypermesh有限元分析前处理流程图
Fig.7 Pretreatment flow chart for finite element analysis based on Hypermesh

图8 划分完网格后的橡胶悬置简化模型
Fig.8 Simplified model of rubber mount after meshing

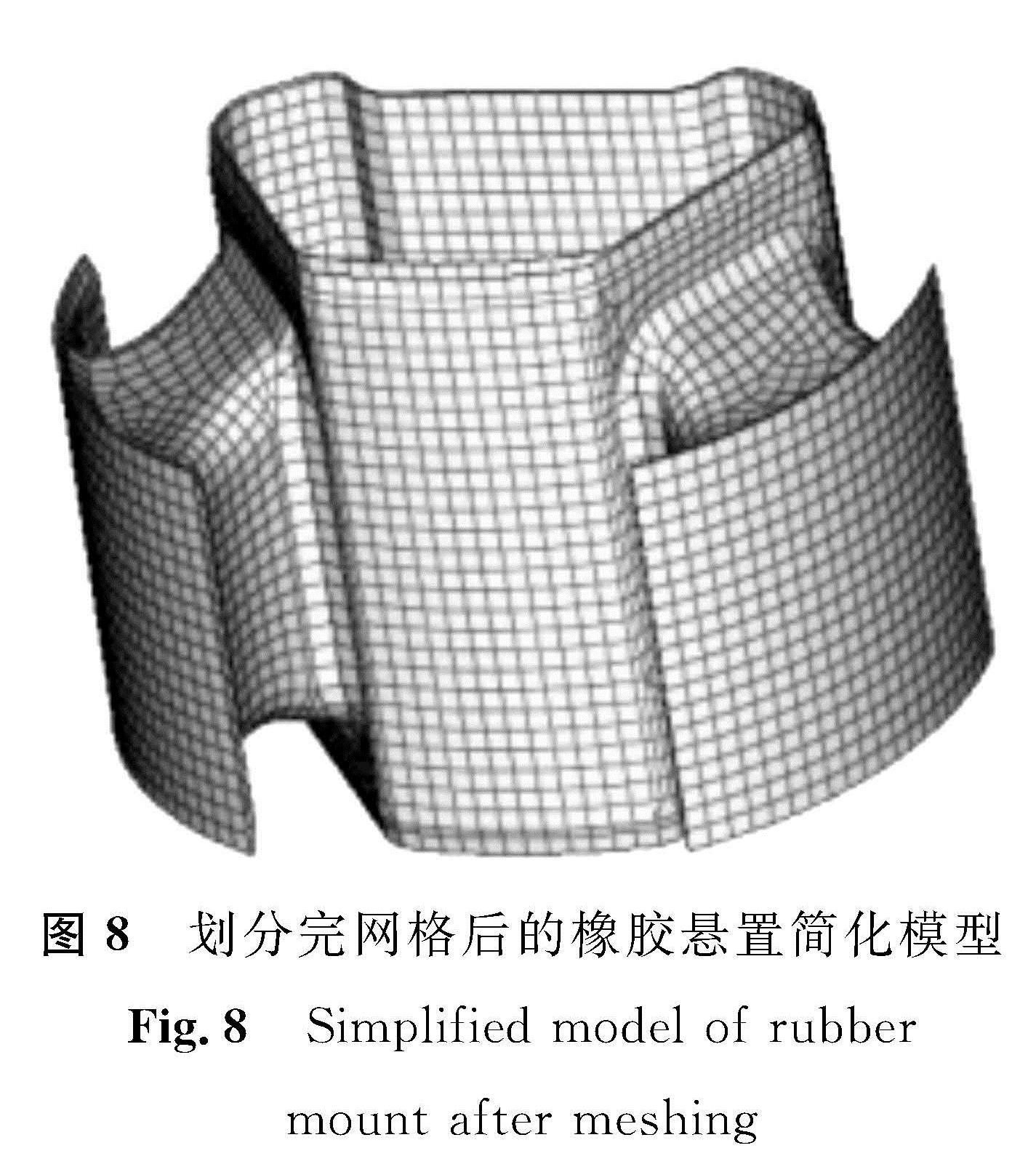
仿真试验的目的是计算橡胶悬置的线性静刚度,悬置线性静刚度一般是在小位移加载下测试得到的,其大小主要由橡胶胶料类型和主簧结构决定。而试验所选用的橡胶悬置结构较为复杂,因此对模型进行了相应的简化,去掉大小2个撞块,保留了主簧部分。将简化后的橡胶悬置模型进行网格划分。网格类型的选择也与仿真试验结果的准确性密切相关,四面体网格相对于六面体网格,单元较少。而六面体网格允许比四面体网格有一个更大的纵横比,因此,为减少应力集中的程度,应尽可能地采用六面体网格。图8为划分完网格后的橡胶悬置简化模型,该模型有12 053个单元,其中六面体单元有11 330个,占单元总量的94%,满足仿真试验计算的精度要求。

在完成几何清理和网格划分之后,将模型导入Abaqus软件中定义橡胶模型参数。施加耦合约束、边界条件和荷载。采用的橡胶模型参数正是单轴拉伸试验中较为接近标准值的试验数据,即C₁₀=0.289,C₀₁=0.044。橡胶悬置大多数硫化在金属内外管上,而金属材料的刚度远远高于橡胶材料,因此将金属外管采用刚性处理,同时在悬置模型弹性中心位置设置一个关联点,刚性连接橡胶内壁金属管,该关联点即为模型的加载点。为保证仿真试验结果的准确性,采用位移加载的形式进行静刚度值预测计算,在仿真试验中分别对悬置X、Y、Z三向加载3 mm的位移,设置加载速度为0.15 mm/s,该加载速度足够慢,可以较好地体现出橡胶材料的超弹性,同时降低橡胶粘弹性对其静态特性的影响。仿真试验的加载情况与实测加载情况保持一致。

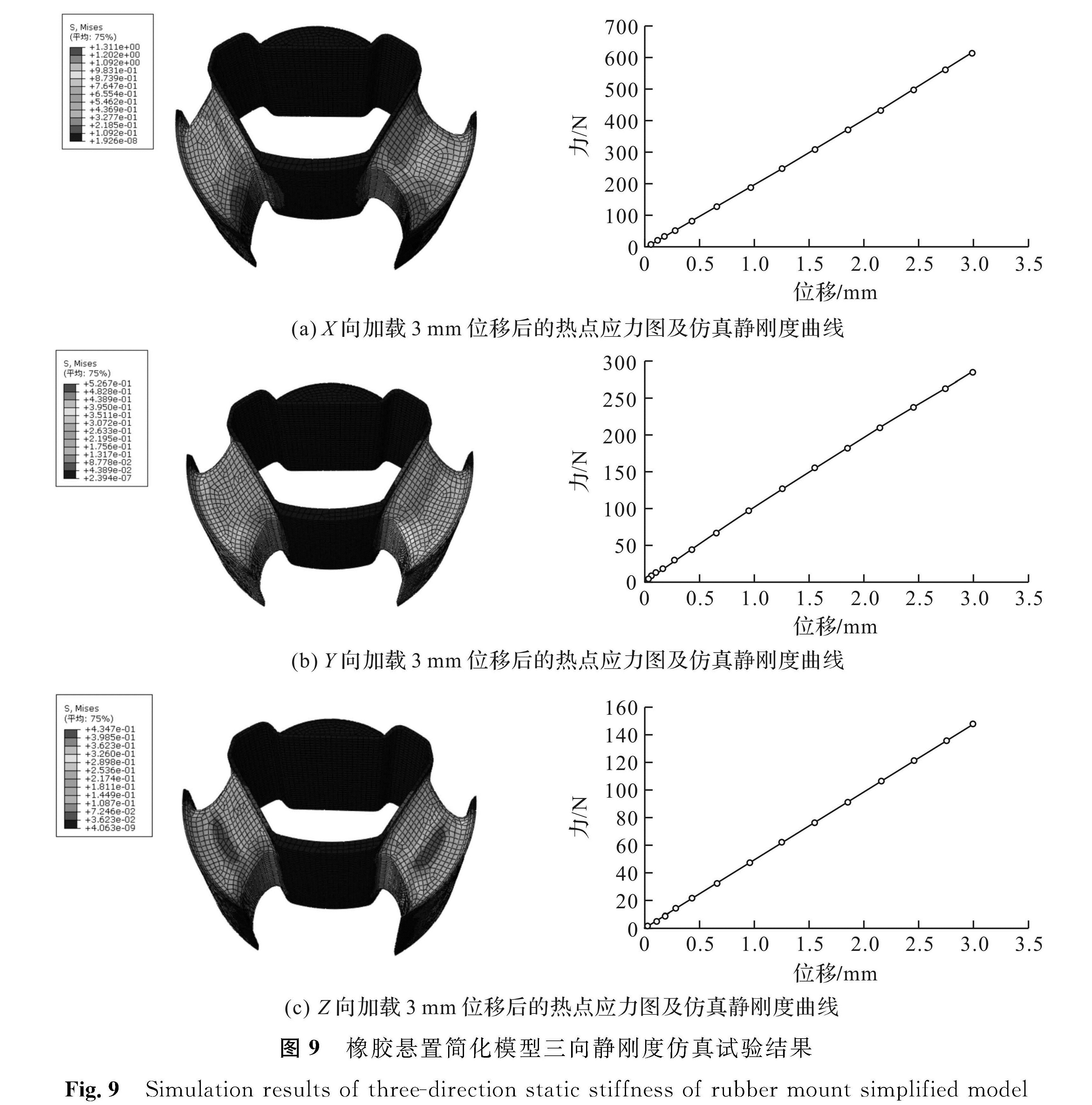
经过Abaqus软件仿真试验得到橡胶悬置简化模型的热点应力图及静刚度数据,将数据整理后绘制出力-位移曲线图,如图9所示。从图9中不难发现,处在小应变范围内悬置的力-位移曲线基本上是一条直线,求其斜率则可以获得橡胶悬置简化模型的预测静刚度值。由此计算出简化悬置X向静刚度为204.09 N/mm,Y向静刚度为95.34 N/mm,Z向静刚度为49.41 N/mm。

图9 橡胶悬置简化模型三向静刚度仿真试验结果
Fig.9 Simulation results of three-direction static stiffness of rubber mount simplified model

橡胶悬置的静刚度测量在MTS700Hz动态仪上进行,该动态仪可进行弹性体单轴动静态特性测试与弹性体单轴耐久性试验,是公认的具有较高试验精度的设备。整套测试系统除动态仪外还包括计算机和用于固定橡胶悬置的特定夹具。

图 10 橡胶悬置静刚度测试
Fig.10 Static stiffness test of rubber mount

为保证有限元分析结果与实际测试结果对比有参考性,实测样件选用与有限元分析模型同款的橡胶悬置,在测试过程中不对悬置作缩径和预加载处理,测试荷载范围为对X、Y、Z三向均加载3 mm的位移,试验温度保持在(23±5)℃。橡胶悬置静刚度实测如图 10所示。

在试验准备阶段,将仪器通电,在计算机上打开静刚度测试软件,预热压力油到正常工作温度,将油源压力调到高压; 将被测悬置通过特定夹具安装在动态仪上,随后开始试验。由于橡胶材料具有马林斯效应,因此,在进行实测时需要进行两次预循环加载来保证试验数据的准确性。悬置静刚度实测的加载方式同样采用以0.15 mm/s的速度加载,传感器上所采集的力-位移数据随之被记录到计算机。试验重复进行3次。

试验结束后将计算机收集到的3次试验的数据进行处理,对力-位移曲线中线性段部分求其斜率即可获得悬置实测静刚度值,将3组实测静刚度值的平均值作为最终实测结果以确保试验结果的精度,结果见表3。

表3 橡胶悬置实测三向静刚度值
Table 3 Measured three-direction static stiffness of rubber mountN·mm-1

至此已获得该款橡胶悬置的预测静刚度与实测静刚度,将两组数据汇入表4进行对比分析,表中相对误差为预测静刚度与实测静刚度之差与实测静刚度的比值。从表4可以看出,对该款悬置三向静刚度的预测结果与实测结果基本上吻合但仍有一定的偏差,其主要原因是对橡胶材料的基础力学试验仅进行了单轴拉伸试验,导致曲线拟合得到的Mooney-Rivlin模型参数偏小,由此造成静刚度预测值均略低于实测值的情况。

表4 橡胶悬置预测与实测静刚度值对比
Table 4 Comparison of static stiffness values between predicted and measured rubber mount

本研究从橡胶材料的本构模型原理入手,通过选用Mooney-Rivlin模型,利用橡胶单轴拉伸试验来获得本构模型参数,随后通过Hypermesh软件对衬套类橡胶悬置的三维模型进行有限元分析前处理,借助Abaqus软件获得橡胶悬置的三向仿真静刚度曲线从而计算出其三向静刚度的预测值。同时,在试验台上对同款悬置进行三向静刚度测试,对比两者的试验结果不难看出,三向静刚度预测值对实测值的相对误差都在10%以内,即在工程允许的误差限范围内。可见,采用单轴拉伸试验获取本构模型参数,结合有限元分析获取衬套类橡胶悬置预测静刚度的方法是可行的。根据该方法可以有效地对某种采用新型胶料或混合胶料的衬套类橡胶悬置进行静刚度预测,这对企业进行悬置类产品的改进与开发有一定的帮助。