离心泵应用领域极为广泛,在生产制造中占据着重要位置[1]。叶轮是离心泵的核心构件,在针对叶轮的优化中叶片包角是一项重要的设计参数,它对水泵性能有着极大的影响[2]。葛书亭等[3-4]利用数值模拟方法对不同叶片内速度场进行大量分析,结果表明叶片存在一个最佳包角值。谢志宾等[5-6]针对离心泵包角对压力脉动展开研究,得到一个适合水泵平稳运行的叶片包角值。牟介刚等[7-8]对包角与水泵特性变化关系展开研究,同时加入了抗气蚀性能的设计因素,从而完善了包角的选择理论。但是,针对中转速比离心泵叶片包角选值研究相对较少,故本研究以一台转速比为129的中转速比离心泵为研究对象,在其他叶轮参数恒定的情况下,分别设计90°、100°、110°、120°、130° 共5种包角的叶轮。利用Fluent仿真软件对不同包角叶轮进行非定常数值模拟分析,得到不同包角叶轮的扬程、效率数值及内部流场分布云图。通过在流道及蜗壳内布置测点得到对应点压力的脉动特性,总结水泵内部流场及压力脉动变化规律。
1 计算模型的建立
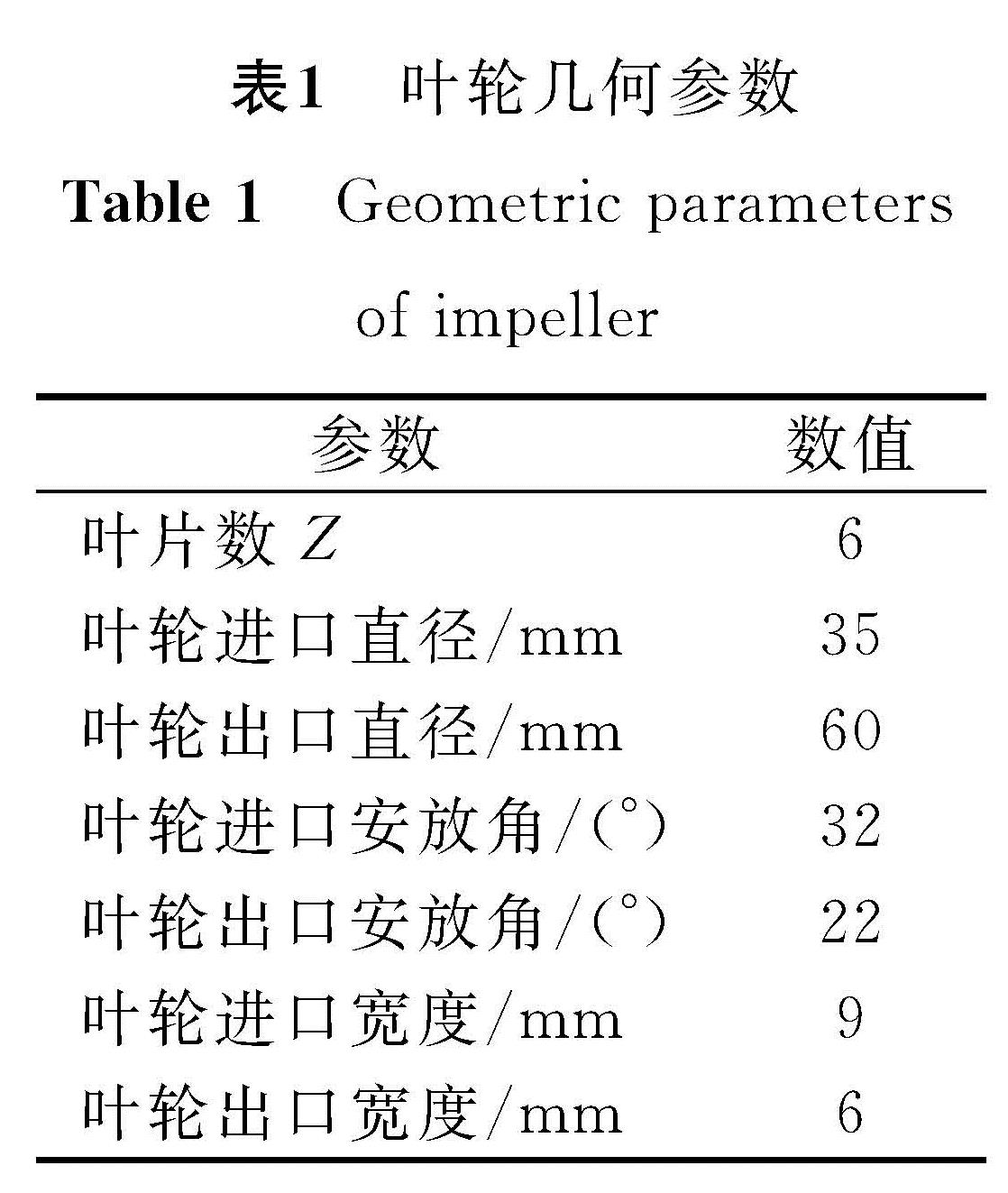
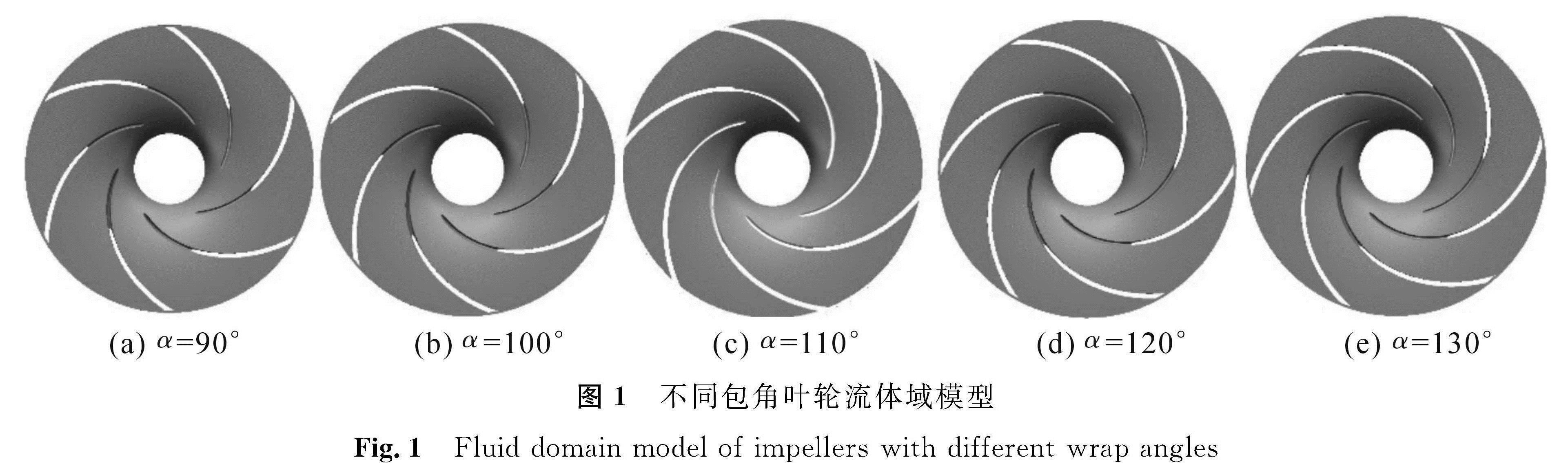
研究对象为一台转速比ns为129的单级单吸式离心泵,额定流量qv为4.8 m3/h,设计扬程H为4.5 m,额定转速n为3 000 r/min。叶轮几何参数见表1。在保持叶轮其他设计参数不变的前提下,对叶片包角α分别设计为90°、100°、110°、120°、130°,根据叶轮其他参数进行三维建模。计算流体力学数值模拟需将水泵模型进行流体域划分,且为确保仿真精度与真实性,需在水泵进出口处各增加一段圆柱形流体域以延长进出口流动路径,使得流体在进出口处充分扩散进而将进出口对流体的影响降至最低[9]。不同包角叶轮流体域模型如图1所示,离心泵全流道流体域模型如图2所示。
2 数值模拟方法2.1 模型网格划分
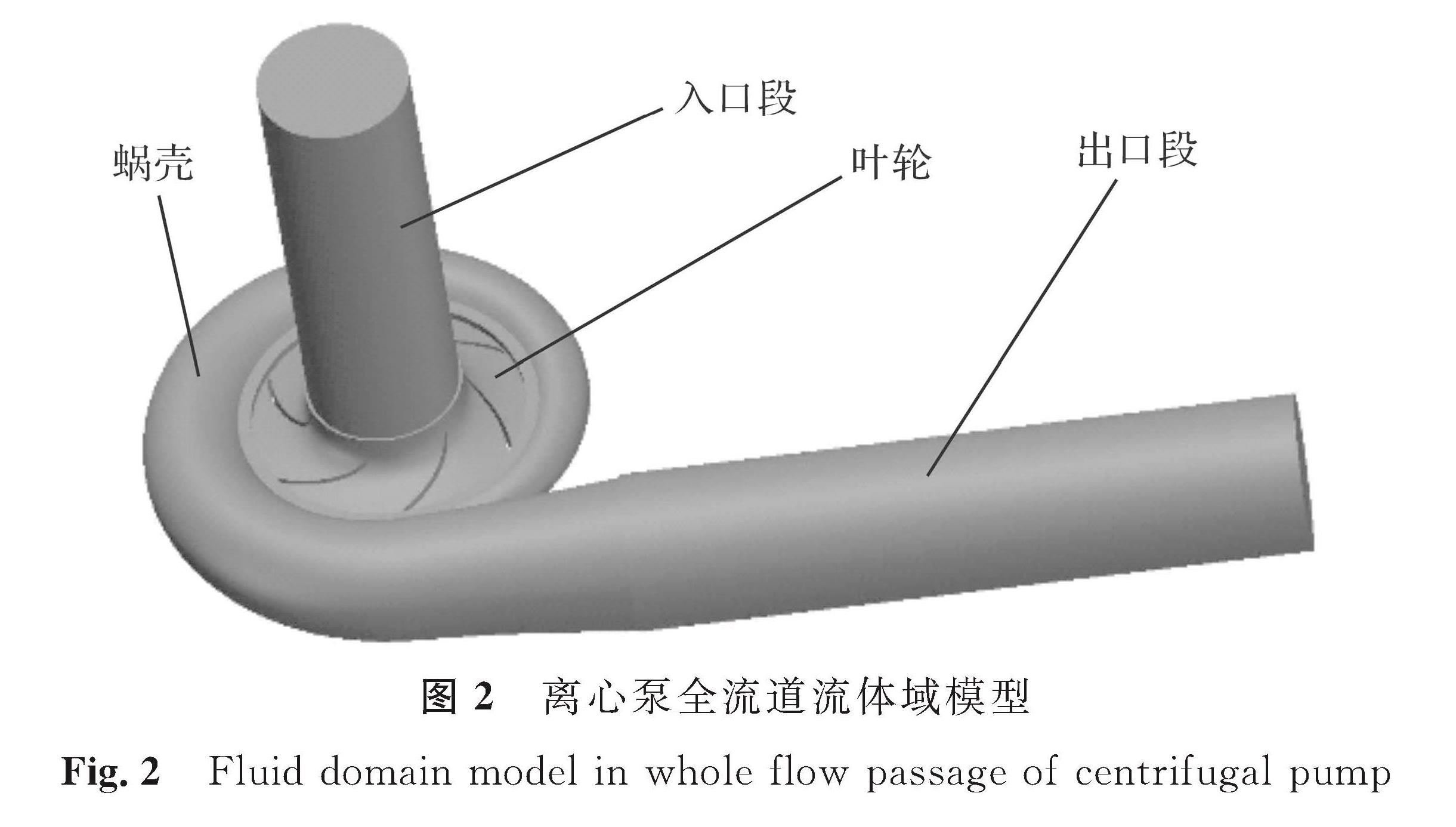
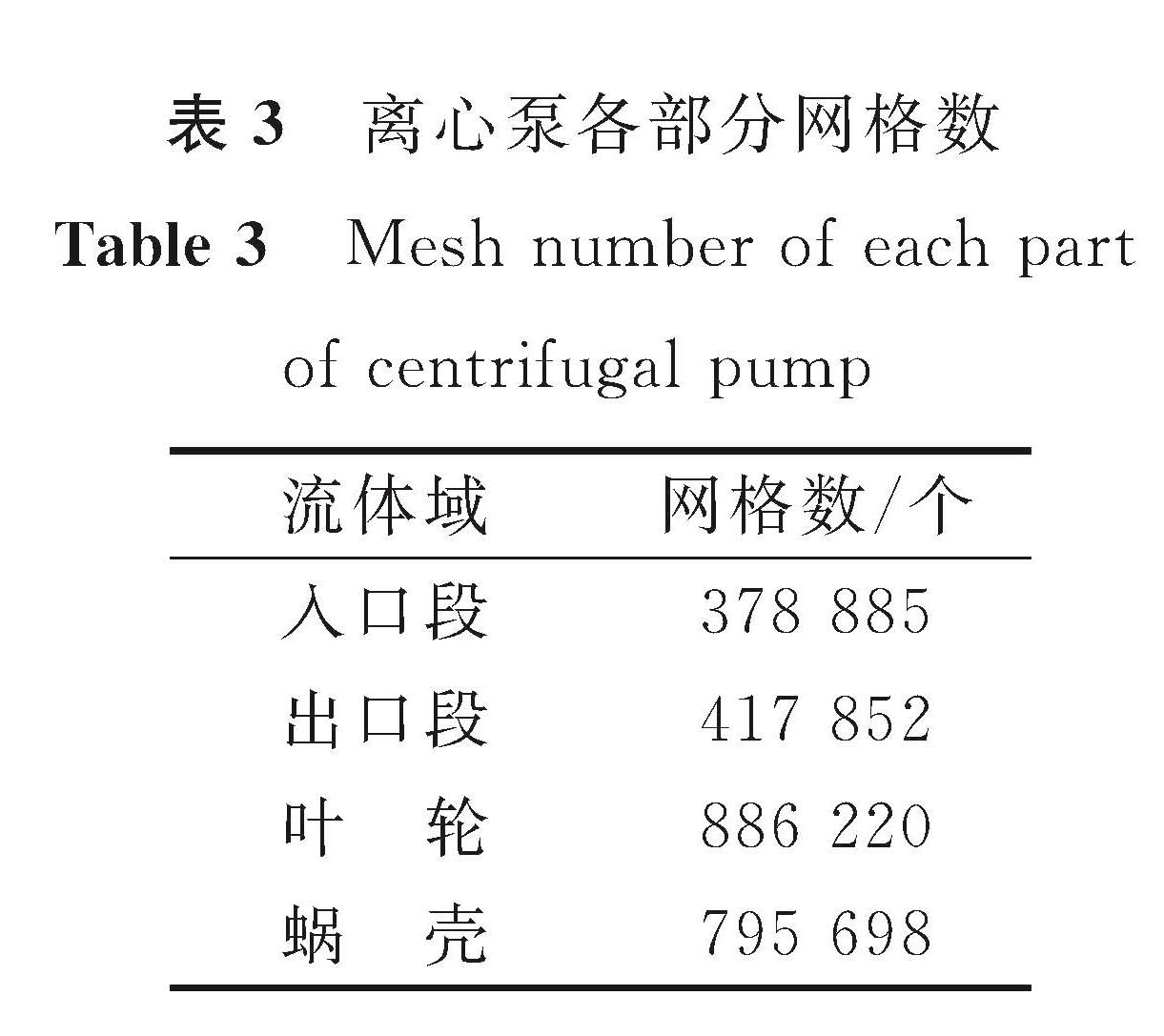
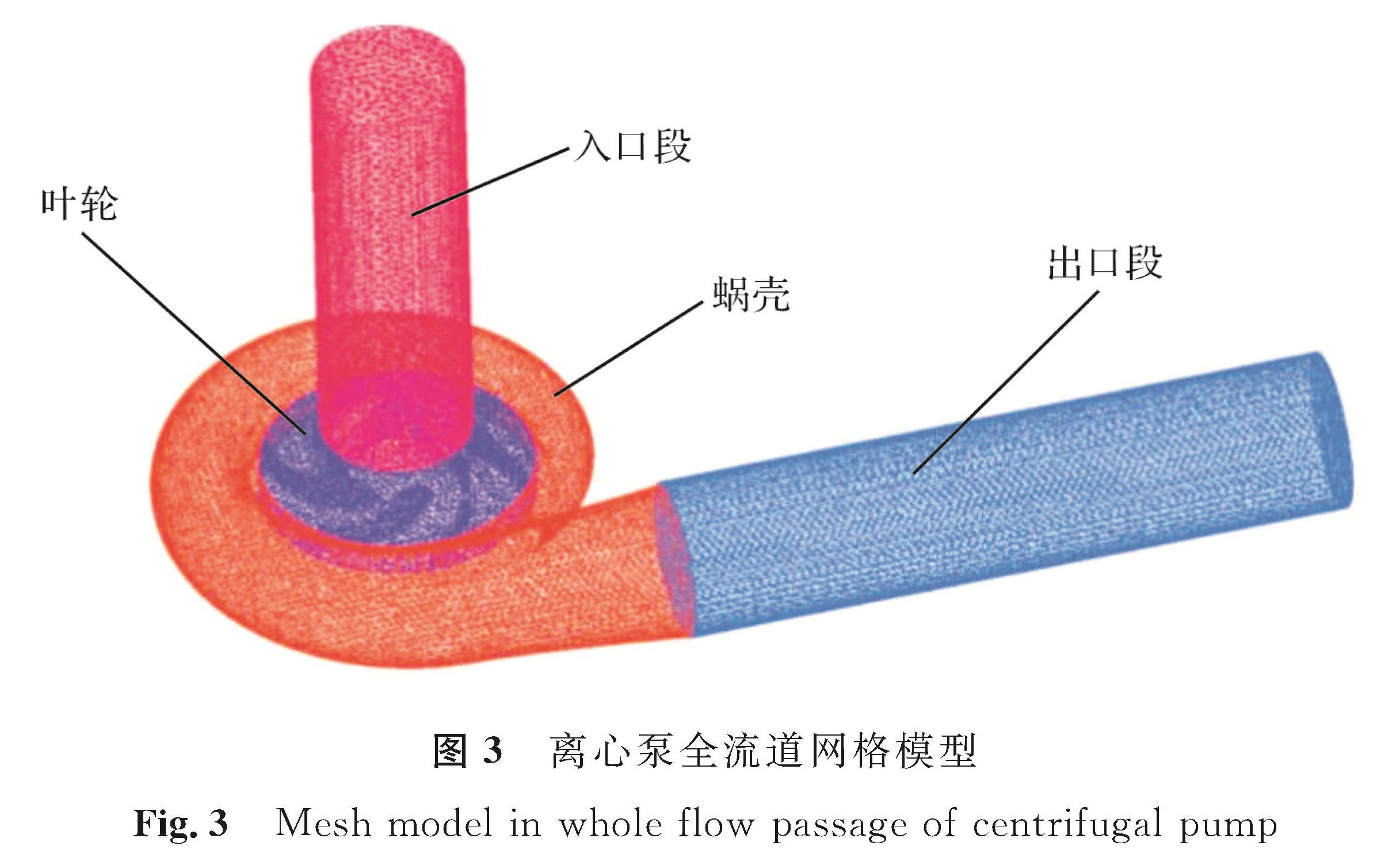
网格划分的质量直接影响仿真精度及收敛程度的计算[10]。使用网格划分软件,利用非结构化四面体网格能较好适应叶轮及蜗壳的过渡性曲面。在蜗壳突变处、蜗舌狭小区域及叶轮较小表面进行局部加密操作能进一步合理划分网格,进而减少收敛误差以保障仿真精度。模型总网格数量过少会使网格质量较差导致模拟失真甚至无法收敛的情况发生,模型网格密度越小越接近真实情况,但此时网格数量会极其多,受计算机性能限制,需进行网格无关性验证以选择最佳网格数量[11]。以90°包角叶轮为例进行网格无关性验证(表2),当模型网格总数约为50万个时,由于网格质量较低导致模拟计算未收敛; 当网格总数约为100万个及200万个时,扬程最大相对误差为23.1%,未满足无关性要求; 当网格总数约为250万个及以上时,扬程最大相对误差仅为1.68%,此时可忽略网格数量带来的误差影响。为了节省模拟仿真收敛时间,最终决定采用247万个左右的网格数量为划分标准。离心泵各部分网格数见表3,离心泵全流道网格模型如图3所示。
2.2 边界条件与压力监测点设定
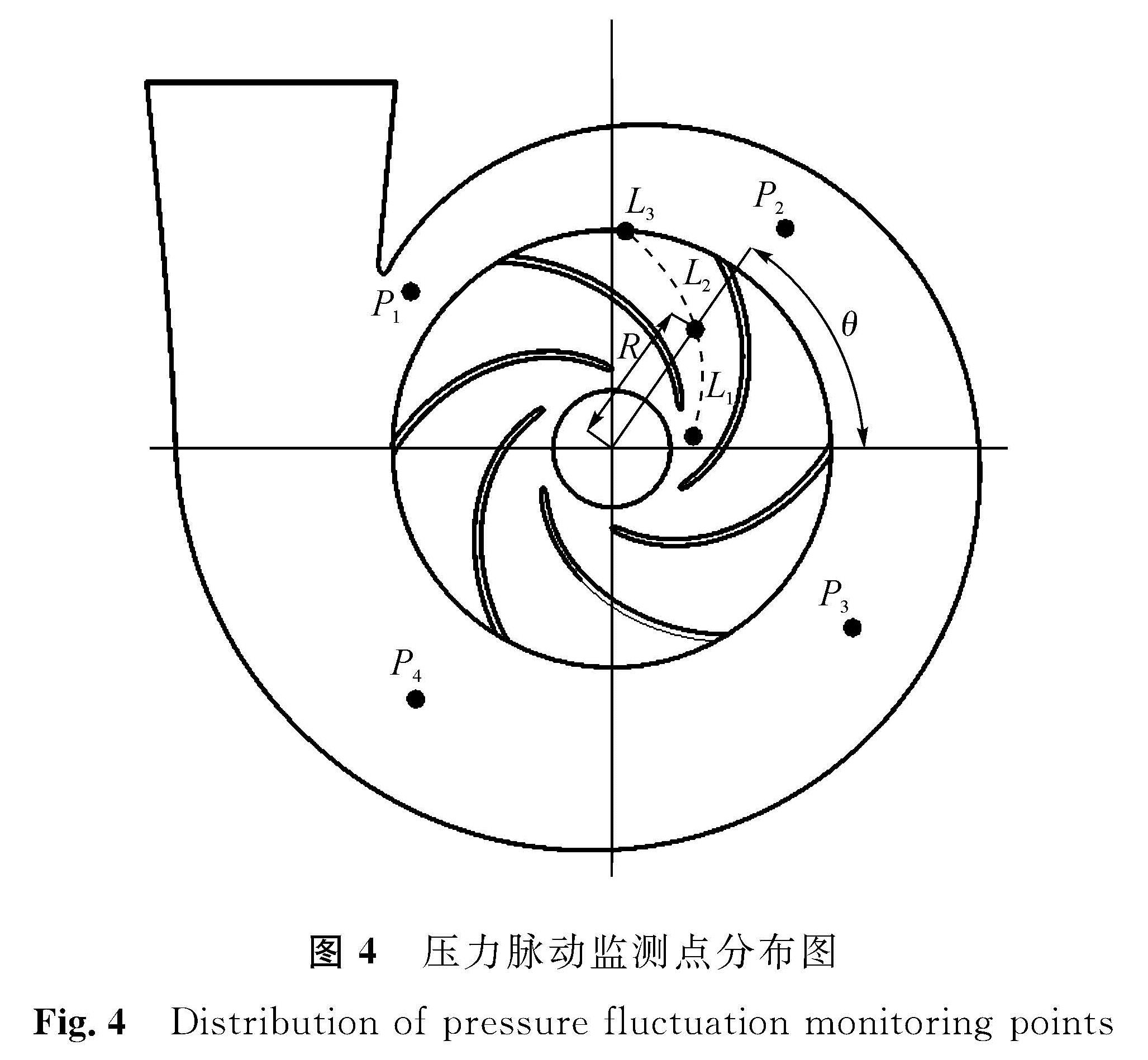
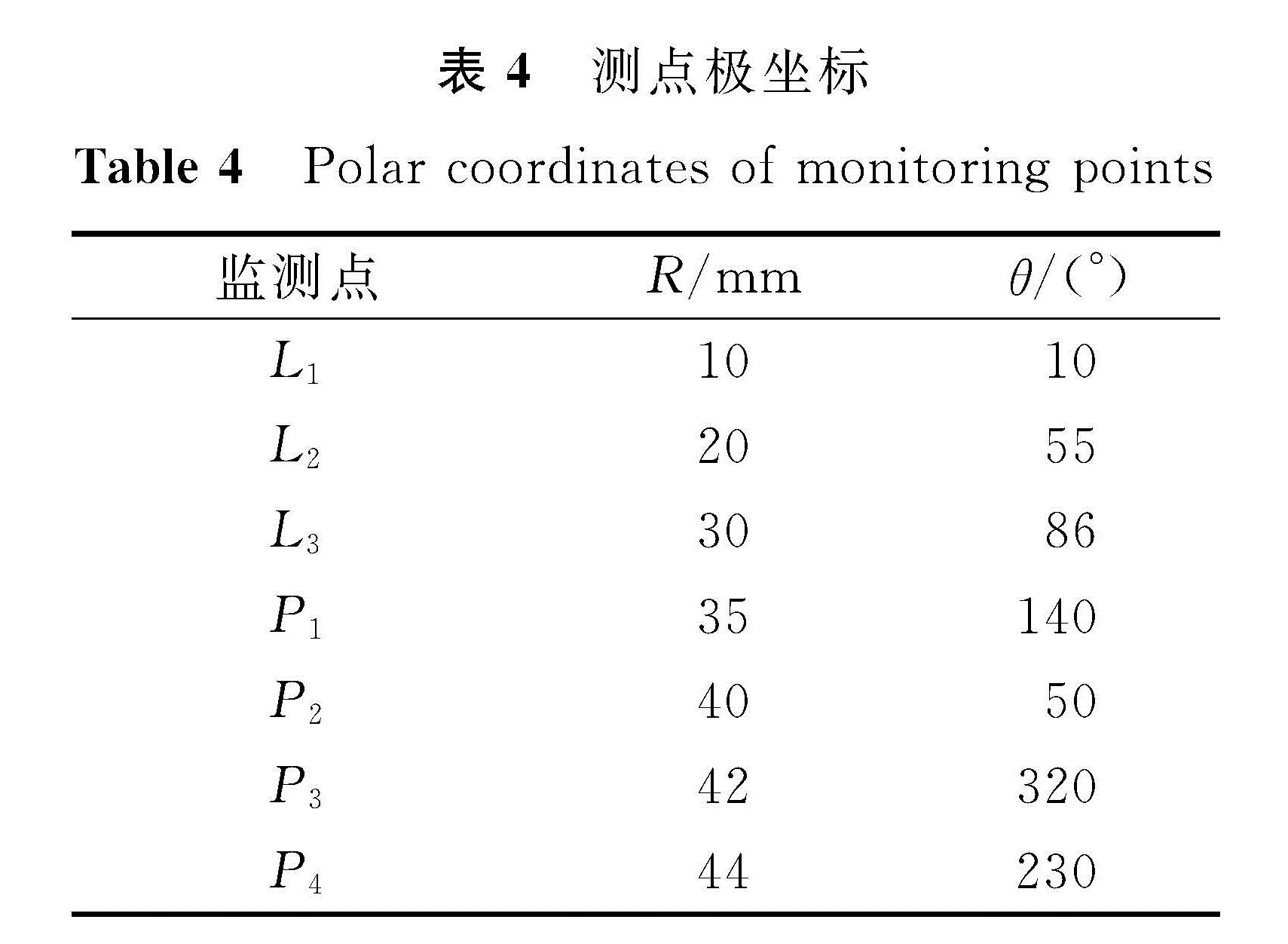
数值模拟使用Fluent软件,选择重整化群(renormalization group,RNG)k -ε。RNG k -ε是一种高雷诺数湍流计算方法,对求解旋转运动中高应变率及流线变化较大的流体运动有着较高的仿真精度,且RNG k -ε模型是对标准k -ε模型的优化,能较准确地模拟动静壁面处的流动特性。流体材料为25 ℃的液体水介质,使用压力耦合方程的半隐相容算法(semi-implicit method for pressure linked equation consistent,SIMPLEC)进行计算,求解精度会进一步提升[12]。收敛条件设置为10-4,对旋转机械采用多重参考系模型(multireference frame,MRF),设置叶轮为转动域,转速为3 000 r/min。入口段、出口段及蜗壳均为固定域,进口设置为速度进口,出口采用压力出口,其余设置保持软件默认[13]。非定常计算中,以首次定常计算结果为初始值。取叶轮每旋转3°的时长为一个时间步,时间步Δ=1.667 10-4 s,每个时间步中最大迭代次数为20次[14]。计算5个旋转周期,总时长t=0.1 s。为避免计算波动,选择最后一个周期作为数据采集周期。同时为研究叶片包角对离心泵压力脉动的影响,在叶轮流道中线处均布L1、L2、L3 3个测点,在水泵蜗壳内均布P1、P2、P3、P4 4个测点。测点位置如图4所示,测点极坐标见表4。
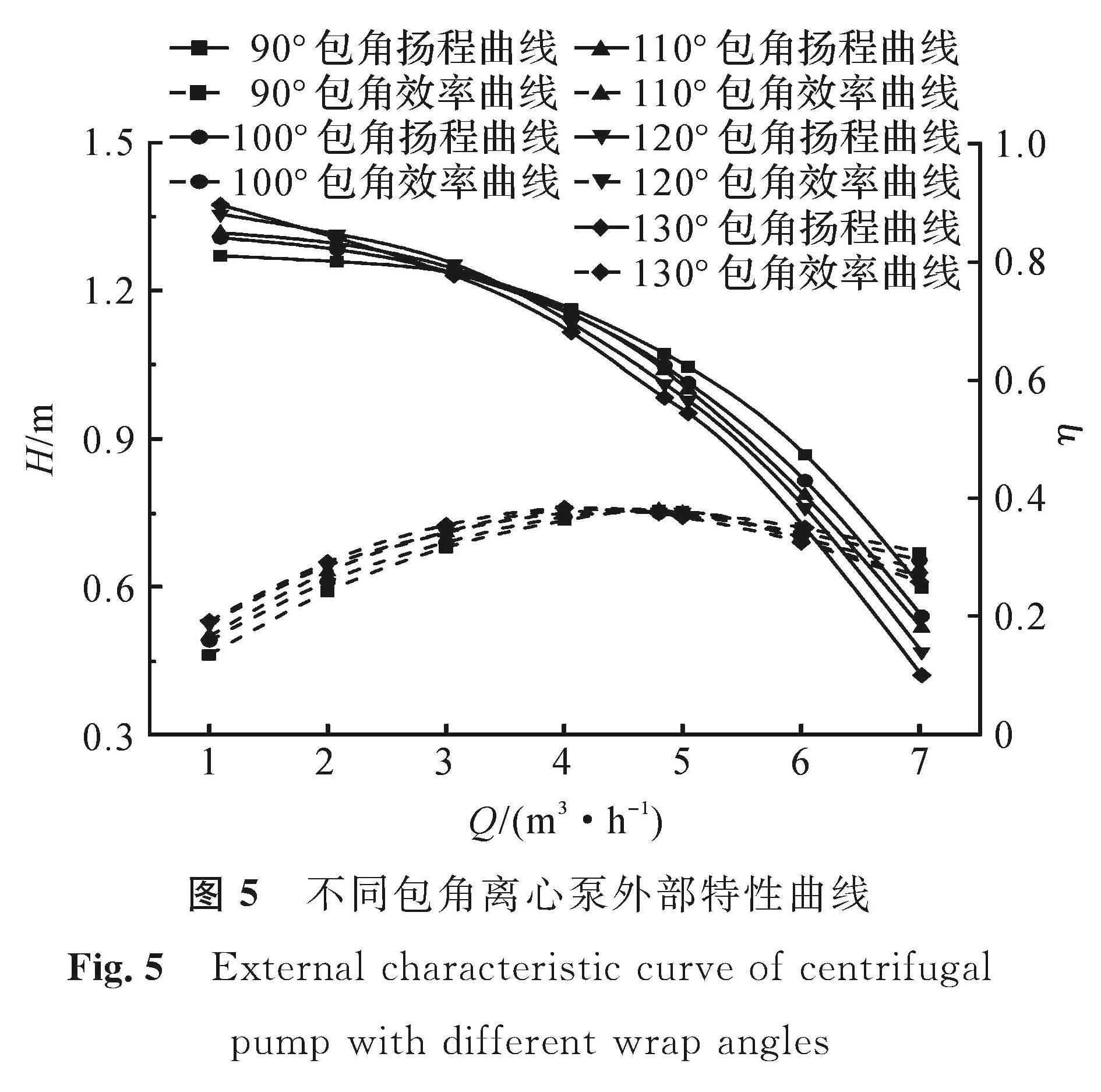
3 仿真结果分析3.1 离心泵外部特性曲线分析
用数值模拟得到的数据计算出不同包角叶轮进出口压力差值。离心泵扬程H与水泵水力效率η[15]计算公式如下:

式(1)~(2)中:P2为叶轮出口压力,Pa; P1为叶轮进口压力,Pa; ρ为流体密度,kg/m3; g为重力加速度,m/s2; Δh为进出口垂直高度差,m; Q为水泵流量,m3/h; M为叶轮轴扭矩,N·m; ω为叶轮轴旋转角速度,rad/s。
图5为不同叶片包角离心泵外部特性曲线图。由图5流量-扬程曲线可知,随着叶片包角的增大,离心泵呈现小流量时扬程上升而大流量时扬程下降的趋势,且包角越大下降趋势越明显,并以额定流量qv=4.8 m3/h为大小流量分界点。随叶片包角增大,额定流量下扬程H降低,且包角增至130°时扬程比包角90°时降低13%。这是由于包角较大时,叶轮喉部的平均安放角减小,导致叶轮的相对液流角逐渐变小,从而使叶轮扬程逐渐降低。由图5流量-效率曲线可知,随着叶片包角增大,离心泵在小流量工况下效率有所提升,而在大流量工况下效率下降较为明显,且包角越大效率下降幅度越大,同时效率最高点也逐渐向小流量方向偏移。额定流量下,130°包角时的效率比90°包角时下降5.2%。这是由于随着叶片包角的增大,叶轮流道逐渐变得狭长,叶片对流体的约束能力增强,流体运动更符合叶片形状流动,也更趋于平缓。但同时叶片表面对流体的摩擦损失也逐渐增大,从而导致水泵效率降低。分析图5曲线趋势可知,较小的叶片包角可得到较高的水泵扬程及效率,但过小的叶片包角会使流道对流体的约束力不足,减少叶片的有效部分,导致水泵效率降低,因此必存在一个较合适的叶片包角使水泵性能达到最佳状态。
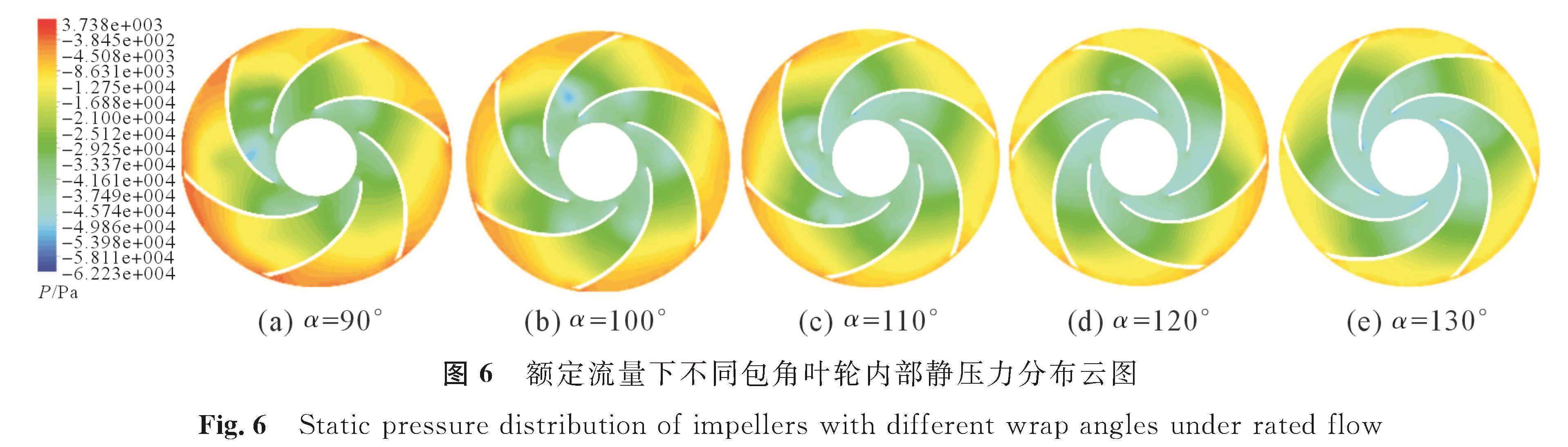
3.2 离心泵内部流场分析3.2.1 叶轮静压力分布云图图6为在额定流量下不同包角叶轮内部静压力分布云图。由图6可知,各叶轮静压力均从进口至出口逐渐增大,这是由于叶轮旋转时对流体做功的结果。随着叶片包角的增大,叶轮进口低压区域变大而出口高压区域减少。其原因是包角增大使得叶片型线变平顺,更贴合流体运动,从而减少了脱流现象的发生; 但过大的包角会产生较大的摩擦,进而降低水泵的扬程与效率。
图6 额定流量下不同包角叶轮内部静压力分布云图
Fig.6 Static pressure distribution of impellers with different wrap angles under rated flow
3.2.2 叶轮速度分布云图
图7为额定流量下不同包角叶轮速度分布云图。由图7可知,叶轮内的速度分布是不完全均匀的。叶轮内低速区主要集中在叶片的工作面,随着包角的增大低速区逐渐减少,叶片背面及叶轮出口的速度逐渐增大。这是由于包角的增加,减少了流道内的当量扩散角,叶片对流体的束缚力增强,但同时大包角会使流道变窄,进而增加了叶轮的摩擦损失。
图7 额定流量下不同包角叶轮速度分布云图
Fig.7 Velocity distribution of impellers with different wrap angles under rated flow
3.3 压力脉动特性分析
由于流体的黏性、惯性及叶轮与蜗壳间的动静干涉造成水泵内出现一种周期性的压力脉动,这种规律性的脉动冲击会造成水泵运行不稳定[16]。为研究中转速比离心泵压力脉动特性,对图4布置的各监测点的压力数据采用无量纲处理,引入压力系数Cp[17],其计算公式如下:

式(3)中:Δp为各点实测压力与平均压力之差,Pa; ρ为流体密度,kg/m3; u2为叶轮出口圆周速度,m/s。
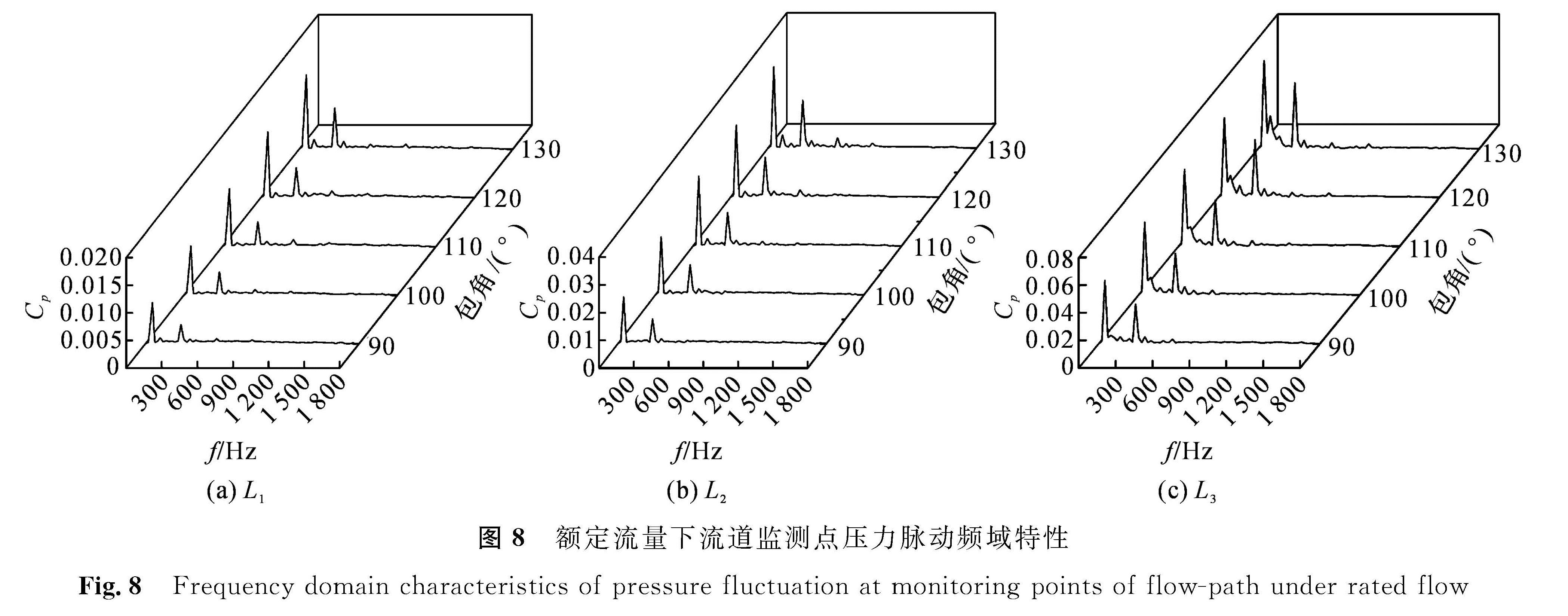
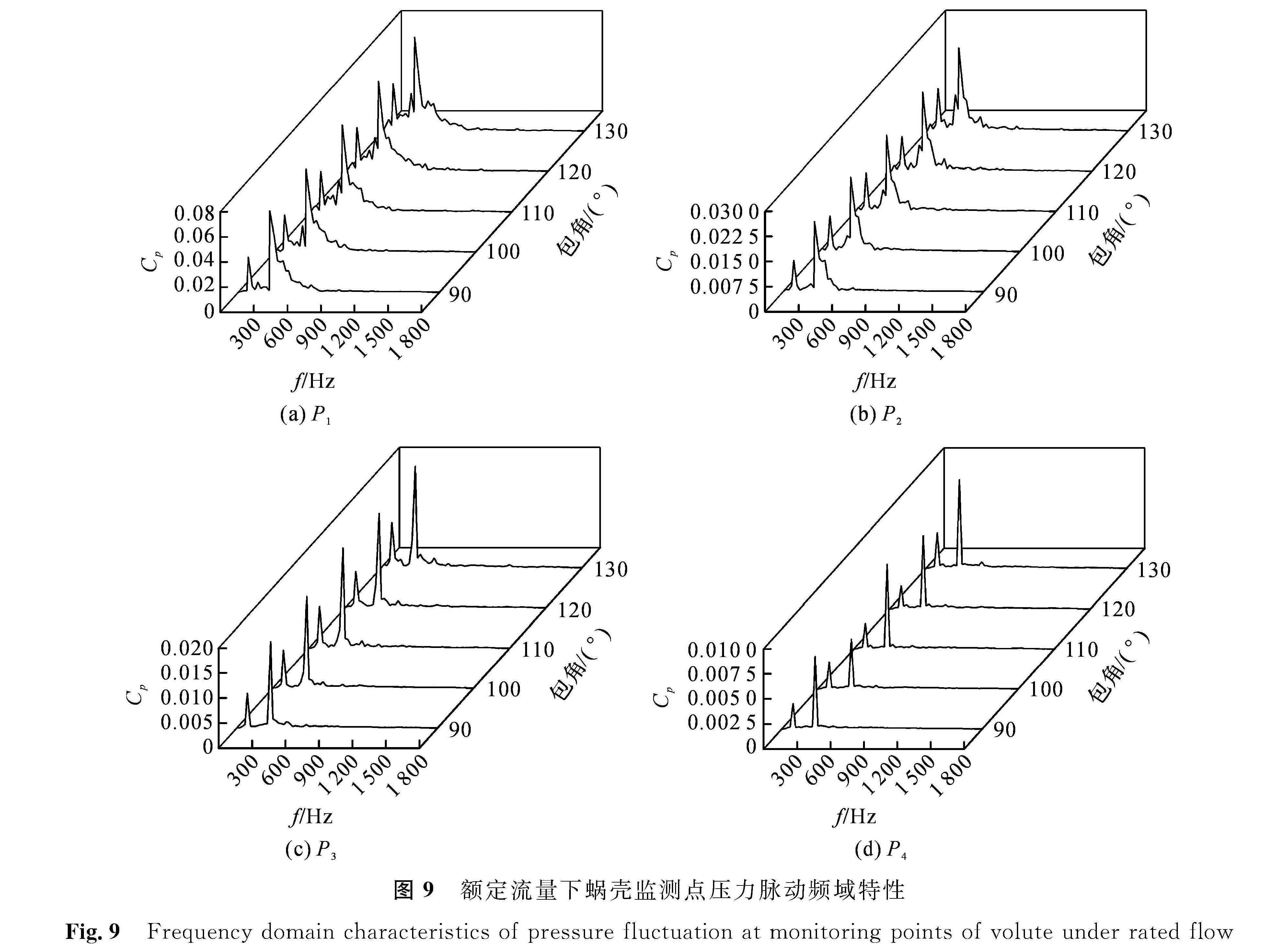
本研究的中转速比离心泵额定转速n为3 000 r/min,故泵转动频率为50 Hz。泵叶片数Z为6,故叶频为300 Hz。将计算得到的压力系数Cp进行快速傅里叶变换,从而得到不同包角下各点的压力脉动频域图。图8为额定流量下叶轮流道监测点压力脉动频域特性图,图9为额定流量下蜗壳内监测点压力脉动频域特性图。
图8 额定流量下流道监测点压力脉动频域特性
Fig.8 Frequency domain characteristics of pressure fluctuation at monitoring points of flow-path under rated flow
由图8可知,在额定工况下流道内各点脉动主频以一倍转频为主,次频以一倍叶频为主; 随着叶片包角的增大,各点脉动幅值均有所提高; 相同叶片包角情况下沿流体流动方向,各测点主频与次主频幅值均明显提高且低频段波动增多,出现叶频代替转频成为主频的趋势。这是由于流道外侧监测点L3最靠近蜗壳,受蜗壳与叶轮间的动静干涉作用影响最大,并且由于前段脉动在蜗舌处消散不及时,第二波脉动在此重叠,使得L3点经过蜗舌处时再次受到脉动影响,这是导致L3点在低频段波动增加的主要原因。
图9 额定流量下蜗壳监测点压力脉动频域特性
Fig.9 Frequency domain characteristics of pressure fluctuation at monitoring points of volute under rated flow
由图9可知,额定工况下蜗壳内监测点频率集中在0~900 Hz,脉动主频约为一倍叶频,次主频约为一倍转频。随着叶片包角的增大,主频与次频幅值均整体呈上升趋势,但120°包角时压力脉动幅值略有所降低,尤其在接近水泵出口P4的点降低较为明显; 相同叶片包角情况下沿P1、P2、P3、P4方向,脉动幅值逐渐减弱,其中P1点脉动最为剧烈,P4点脉动最弱。这是由于P1最靠近蜗舌,蜗舌处径向P4间隙较小,蜗壳与叶片动静干涉最为强烈,随着监测点向P4点移动,逐渐远离蜗舌,径向间隙变大,故压力脉动逐渐减弱。
4 结 论以一台比转速为129的中转速比离心泵为研究对象,通过数值模拟对比分析5种不同包角叶轮的水泵外部特性、内部压力与速度分布及压力脉动特性,得出以下结论:
1)随着叶片包角的增大,离心泵的扬程和效率均有所下降且效率最高点向小流量方向偏移。130°叶片包角相比90°包角时扬程及效率分别降低13%与5.2%。
2)额定工况下,叶片包角的增大导致叶轮进口低压区面积增大,而出口高压区面积减少,流体更贴合叶片流动,进而减少了脱流现象的发生。
3)额定工况下,低速区主要分布在叶片工作面,高速区集中在叶轮出口及叶片背面处。随着叶片包角增大,低速区域逐步减少,出口速度明显上升。
4)离心泵压力脉动特性受蜗舌影响较大。额定流量下蜗壳压力脉动主频约为一倍叶频,叶轮流道内压力脉动主频约为一倍转频。随着叶片包角的增大,各点主次频均整体呈现上升趋势,其中130°包角时各点压力脉动幅值最大。相比其他大包角,120°包角时压力脉动幅值略微降低。综合分析离心泵外部特性、流场特性及脉动特性,于是可取120°作为中转速比离心泵最优包角。
- [1] 周强,李宏坤,仲作文,等.离心泵导叶流道进口处压力脉动研究[J].工程热物理学报,2020,41(7):1679.
- [2] 刘意,王淑红,李华聪,等.叶片包角对组合叶轮离心泵工作特性的数值研究[J].科学技术与工程,2015,15(8):244.
- [3] 葛书亭,宋文武,符杰,等.叶片包角对低比转速离心泵性能的影响[J].水泵技术,2015(5):13.
- [4] 黄茜,袁寿其,张金凤,等.叶片包角对高比转数离心泵性能的影响[J].排灌机械工程学报,2016,34(9):742.
- [5] 谢志宾,陈二云,丁京涛,等.叶片包角对离心泵流场及脉动特性的影响[J].上海理工大学学报,2017,39(5):430.
- [6] 杨泽江,宋文武,万伦.叶片包角对中比转速离心泵水力振动的影响研究[J].水力发电,2020,46(5):79.
- [7] 牟介刚,施郑赞,谷云庆,等.叶片包角对离心泵空化性能的影响[J].浙江工业大学学报,2019,47(1):24.
- [8] 万伦.叶片包角与出口安放角对中比转速离心泵性能的影响研究[D].成都:西华大学,2019.
- [9] 万伦,宋文武,虞佳颖,等.叶片包角对高比转速离心泵水力性能的影响研究[J].人民长江,2018,49(15):98-99.
- [10] 高振军,付威,刘建瑞,等.叶片包角对双吸泵内部流场及水力性能的影响研究[J].中国农机化学报,2019,40(7):85.
- [11] 周晓红,曾维友,陈伟,等.汽车冷却水泵小流量工况下非定常空化特性研究[J].机电工程,2019,36(8):777.
- [12] 裴迎举,宋文武,胡帅,等.多工况下不同叶片包角的斜流泵水力特性研究[J].水利水电技术,2017,48(9):139-140.
- [13] 杨华,刘超,汤方平,等.不同叶片包角的离心泵试验与数值模拟[J].机械工程学报,2007(10):166-168.
- [14] 戴菡葳,刘厚林,丁剑,等.离心泵叶轮出口宽度对泵腔内压力脉动分布的影响[J].排灌机械工程学报,2015,33(1):22-23.
- [15] 赵伟国,翟利静,咸丽霞,等.叶轮出口宽度对离心泵性能及压力脉动的影响[J].兰州理工大学学报,2020,46(2):64-65.
- [16] 周晓红,曾维友,陈伟,等.叶顶间隙对汽车水泵压力脉动影响的数值研究[J].流体机械,2018,46(8):30-31.
- [17] 杨敬江,李先军,潘中永,等.双蜗壳离心泵空化流动对隔舌处压力脉动特性的影响[J].排灌机械工程学报,2020,38(5):448.
 图 1 不同包角叶轮流体域模型
Fig.1 Fluid domain model of impellers with different wrap angles
图 1 不同包角叶轮流体域模型
Fig.1 Fluid domain model of impellers with different wrap angles