近年来,由于STAR(smooth transition autoregression,平滑转换自回归)模型在对时间序列动态中机制转换非线性特征的描述上,具有一般性和灵活性的特点,被广泛应用于汇率^[1]、通货膨胀率^[2-3]、失业率^[4]、股市^[5]等金融与经济领域。在日常生活中,宏观时间序列数据通常具有明显的时间趋势特征,在建模前需对时间序列平稳性进行分析,因此对带线性趋势的时间序列进行单位根检验(检验平稳性)具有广泛的实际意义,进而带趋势项STAR模型的单位根检验受到了国内外研究者的广泛关注^[6-7]。

对带确定性趋势(或者截距)的线性AR(autoregression,自回归)模型的2种表达形式而言,通过对模型化简可知二者具有相同的波动部分,因此对这2种带确定性趋势的AR模型进行单位根检验会得到一致的结论,然而对带确定性趋势项的STAR过程而言,2种形式却包含了不同的波动部分^[6]。如果对这2种形式带趋势项的STAR模型的单位根检验不加以区分,会导致检验结果的不可靠,如Zhang^[8]和Kaufmann等^[9]针对不同形式带趋势项STAR模型进行了线性检验,所得结论不同。目前关于带趋势ESTAR(exponential smooth transition autoregression,指数平滑转换自回归)模型的单位根检验研究较侧重于去趋势的各种方法^[7,10,11],鲜有文献对模型的2种不同形式加以区别研究。因此,我们对ESTAR模型2种形式的单位根检验进行研究,基于模型在不同形式下相应的辅助方程,考察KSS(Kapetanios-Shin-Snell)检验统计量的极限分布,从而对2种形式单位根检验从根本上加以区分,并且还为拓宽对带确定性趋势项STAR模型的单位根检验的研究打下一定的理论基础。

考虑以下一阶带确定性趋势项ESTAR模型:

Δy_t=a+bt+γy_t-1(1-exp{-θy²_t-1})+ε_t,θ>0, (1)

或

y_t=a+bt+e_t,Δe_t=γe_t-1(1-exp{-θe²_t-1})+ε_t,θ>0。 (2)

式(1)～(2)中:误差项ε_t是方差为σ²且sup_tE(ε⁶_t)<∞的鞅差序列。如果式(1)～(2)中γ=0或θ=0,则ESTAR模型简化为AR模型。

Kapetanios等^[12]363证明了当-2<γ<0时,无趋势项的ESTAR模型是全局平稳的,而本文主要研究带趋势项ESTAR模型的单位根检验,即检验带趋势的时间序列是带漂移项的单位根过程(非平稳过程)还是带线性趋势项的平稳ESTAR过程。当时序y_t有非零均值或线性趋势项时,Kapetanios等^[12]364建议先去均值或去趋势项再进行单位根检验,即当y_t=l'd_t+y ^～_t时,其中d_t=1或d_t=(1 t)',则考虑y ^～_t=x_t-l'd_t,其中l为常规最小二乘(OLS)估计量,然后对y ^～_t进行单位根检验。根据泰勒展开,辅助方程为

Δy ^～_t=δy ^～3_t-1+e_t。 (3)

式(3)中:e_t为误差项。进一步,Kapetanios等^[12]363提出了检验H₀:δ=0的t检验(又称KSS检验),检验统计量t_KSS的极限分布为

当y_t具有非零均值或带趋势项时,相应的KSS检验统计量t^μ_KSS,t^τ_KSS的极限分布分别用去均值布朗运动(W^μ(r))或去趋势的布朗运动(W^τ(r))去代替式(4)中的W(r)^[13]362,其中

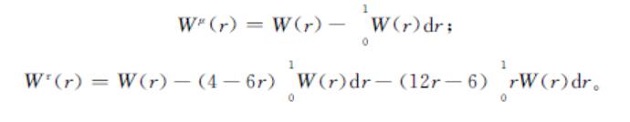
KSS检验统计量的极限分布是基于OLS去趋势方法进行的,即考察的是基于式(2)模型的单位根检验。对式(1)通过泰勒展开可以得到以下辅助方程:

Δy_t=a+bt+δy³_t-1+u_t。 (5)

采用KSS统计量:t=(δ)/(s.e.(δ))来考察式(1)的单位根检验,对应非零均值过程(a≠0,b=0)和带趋势项过程(b≠0)时分别记作t^μ,t^τ。基于辅助方程式(5)进行单位根检验,即检验原假设H₀:δ=0和备择假设H₁:δ<0,以下定理1和定理2给出了t^μ和t^τ的极限分布。

定理1 假设Δy_t=ε_t,则

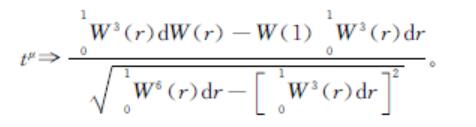
“=>”表示弱收敛。在备择假设下,即基于式(5)(b=0)情况下带均值ESTAR模型的检验统计量t^μ具有一致性,且以速率T(样本量)收敛。

证明:根据辅助方程式(5)(b=0),在原假设H₀下OLS估计量

两边同乘对角阵(T^1/2,T²),有

根据定理1的假设,则在辅助方程式(5)中u_t=ε_t。根据随机积分的弱收敛定理和ε_t的半鞅性质^[14],则有

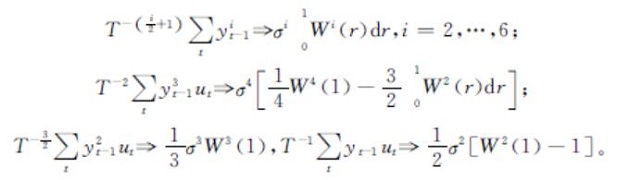
因此我们可以得到

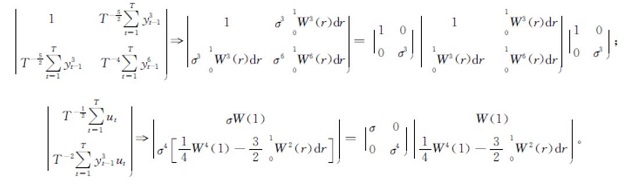
在备择假设下,Δy_t,yⁱ_t-1都是I(0)过程,容易得出t^μ=O_P(T),即以速率T收敛,得证。

文献[8]给出了相应的结论,但没有给出证明。而Kapetanios等^[12]364和Hanck^[13]362给出式(2)的t^μ的极限分布为,通过计算可得极限分布为

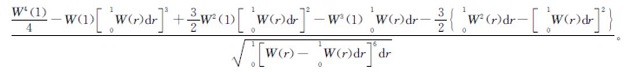
通过对上述极限分布的对比发现,对于具有均值过程的时序,基于式(1)和式(2)的模型检验统计量极限分布不一致,因此临界值不一样,对这2种形式的模型不加以区分,直接用去趋势KSS检验临界值对式(1)进行单位根检验,所得检验结果必定不可靠。

定理2 假设Δy_t=a+ε_t且y₀=0,则

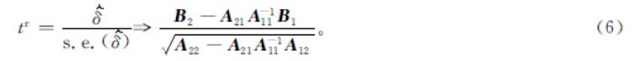
式(6)中:A₁₁、A₁₂、A₂₁、A₂₂和B₁、B₂分别为矩阵A(W(r))、B(W(r))的分块矩阵,具体形式参见以下证明。

证明:在原假设下Δy_t=a+ε_t,y₀=0,则有y_t=at+∑^t_i=1ε_i。这意味着y_t-at和∑^t_i=1ε_i有着同样的收敛性。令y_t-at=z_t,Δy_t-a=Δy^*_t,则辅助方程式(5)为

Δy^*_t=bt+a³(t-1)³+3δ²az²_t-1(t-1)+3δ a²z_t-1(t-1)²+δ z³_t-1+u_t。

不妨记

,则有ΔY^*=Xβ+U。在原假设下(过程为带漂移的单位根过程),β的OLS估计量为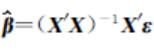,其中ε=(ε₁,…,ε_T)'。根据随机积分的弱收敛定理和ε_t的半鞅性质,则有

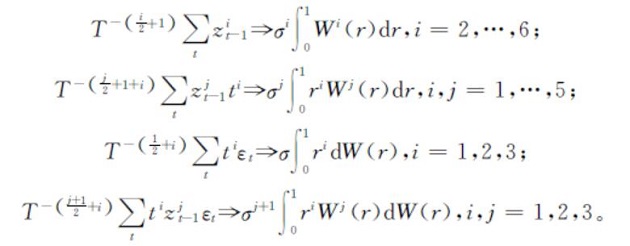
根据连续映射定理,我们可以得到[γ^-1(X'X)γ^-1]=>H(W(r),σ),且[γ^-1(X'ε)]=>Q(W(r),σ),其中

γ为5×5的对角元素(T^3/2 T^7/2 T^5/2 T³ T²)的对角阵。令D(σ)为5×5的对角元素(1 1 σ² σ σ³)的对角阵,E(σ)为5×5的对角元素(σ σ σ³ σ² σ⁴)的对角阵,则有H(W(r),σ)=D(σ)A(W(r))D(σ)和Q(W(r),σ)=E(σ)B(W(r)),其中

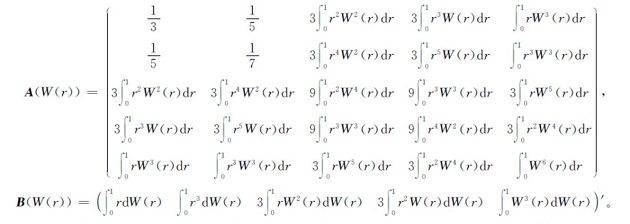
因为在原假设下H₀:δ=0可以写成H₀:Rβ=0,其中R=(0 0 0 0 1),则通过计算可得

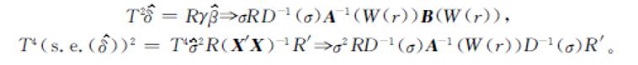
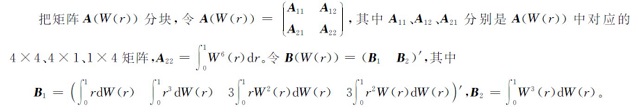
因此,则有

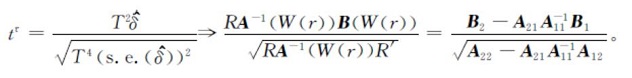
得证。

在上述定理1和定理2中,由于y₀是有界的随机变量或者是常数,其相应的极限分布不变^[15],为了证明方便起见,我们假设y₀=0。基于式(2)的模型在原假设下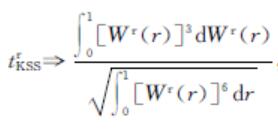,其中W^τ(r)=。对比二者极限分布,发现分子分母均含有W(r)最高次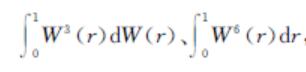,但其他项却不完全相同,基于带趋势项式(1)和式(2)二者单位根检验极限分布并不相同,因此要对这2种情况加以区别对待。

定理1和定理2说明了不同形式带趋势项的ESTAR模型t检验统计量的极限分布并不相同,因此在分析带趋势项过程时,单纯地使用先去趋势然后用常用的临界值表检验法并不十分科学。考虑到带趋势项的非线性ESTAR模型的2种形式导致的波动不一致,本研究从理论角度给出了证明,这一结果为带确定性趋势项ESTAR模型单位根检验的研究提供了理论参考,故建议在采用带趋势项ESTAR模型建模分析数据时,应对采用式(1)还是式(2)加以区分。本研究侧重考虑的是带趋势项ESTAR模型的2种不同形式的极限理论,考察的是常用的线性趋势部分,接下来我们将会把研究进一步扩展到傅里叶趋势^[16]情景中去,以进一步拓宽带趋势项ESTAR模型单位根检验的研究思路。