永磁同步电机由于其优良的功率密度、效率和初始转矩,被广泛用作电动汽车的核心驱动部件[1]。但高功率密度会造成电机严重的温度上升,从而影响工作效率,甚至损坏电机的核心部件。因此需要探寻有效的方法来预测永磁同步电机的温度,以保障电机的安全稳定运行。现有关于永磁同步电机的温度预测方法主要有:温度公式法、参数辨识法和热网络法。温度公式法主要使用计算流体力学中的有限元分析法进行建模,从而实现温度预测[2-3]; 参数辨识法一般通过通量观测和信号注入,根据磁通量和信号的变化预测温度[4-5]; 热网络法的主要代表为集总参数热网络(lumped parameter thermal network,LPTN),通过将热路等效为电路建立网络进行计算,实现温度的预测[6-7]。随着人工智能技术的迅速发展,深度学习在永磁同步电机的温度预测领域得到了应用。相比传统方法,深度学习对永磁同步电机的温度预测,并不需要具备大量电机发热原理相关知识,其预测效果主要取决于数据集的可靠性和模型的性能。2017年,Wallscheid等[8]首次引入长短期记忆(long short-term memory,LSTM)[9]网络来预测永磁同步电机核心部件的温度,其预测精度较高。Kirchgässner等[10]证明了深度残差卷积循环网络在永磁同步电机温度预测方面的可行性,并在试验中加入了贝叶斯优化法优化了超参数。Guo等[11]建立了一种深度神经网络模型用于定子绕组温度的预测,为温度预警系统提供一定的技术支持。在使用循环网络对时间序列进行预测时,部分研究者会使用堆叠的结构来增加模型的深度,包括堆叠的门控循环单元(stacked gated recurrent unit,SGRU),堆叠的长短期记忆网络(stacked LSTM,SLSTM)[12]及不同循环网络组合的堆叠模型[13]等,这类模型包含多个相同或类似的隐藏层,相比单层的循环网络结构具有更强的表达能力及更好的抽象特征提取能力。但是这些方法在面对复杂的时间序列预测任务时,不易确定隐藏层之间的单元数,易造成算子的浪费。
针对永磁同步电机温度预测模型精度有待提升的问题,本研究对门控循环单元(gated recurrent unit,GRU)[14]进行了改进,提出一种新型循环网络嵌套式门控循环单元(nested gated recurrent unit,NGRU)网络,并引入一维卷积神经网络(1D convolutional neural networks,1D-CNN),进一步提出一种用于预测永磁同步电机核心部件温度的深度学习模型——1D-CNN串联NGRU(1D-CNN tandem NGRU,CNGRU)。在本研究中,使用NGRU和CNGRU及其对比模型对永磁同步电机核心部件定子轭、定子绕组和定子齿进行温度预测,并根据试验结果分析论证了NGRU和CNGRU预测的精度和稳定性。
1 方法原理1.1 1D-CNN
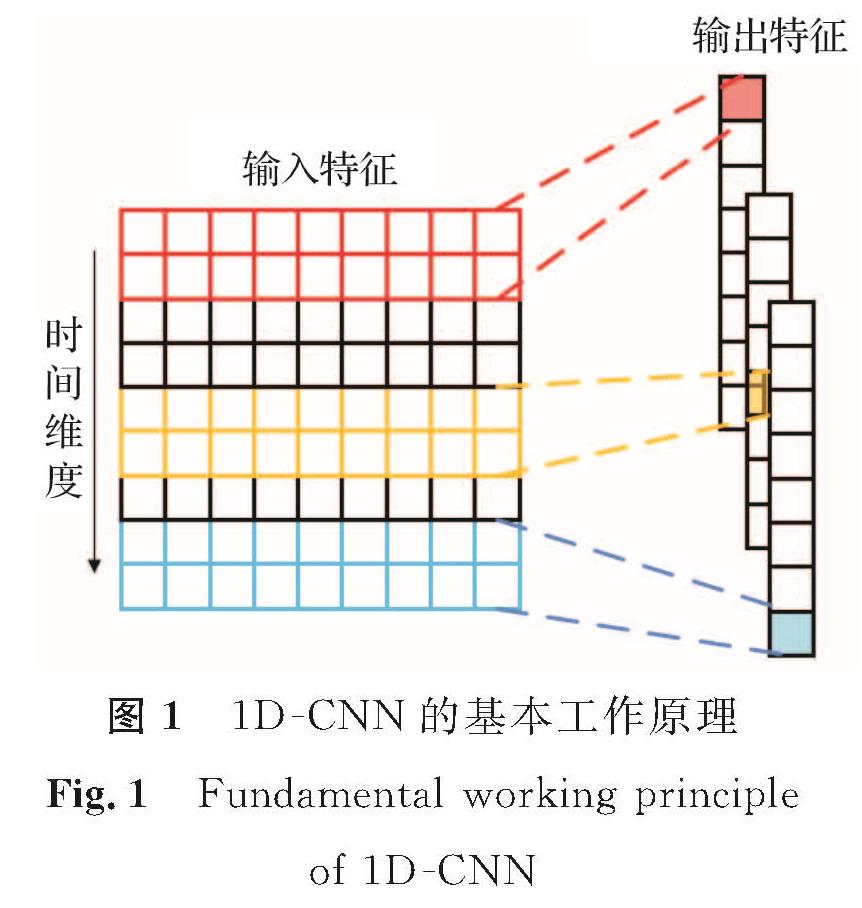
CNN是一种基于局部连接和权值共享的神经网络[15],而1D-CNN的输入通常为一维或二维数组,其卷积核仅在一个方向上进行滑动,在处理时间序列数据领域应用广泛。本研究使用1D-CNN对永磁同步电机的特征进行初步提取,1D-CNN的基本工作原理如图1所示。1D-CNN的基本运算表达式如下:
hk=f((Wk·x)+bk) (1)
式(1)中:hk为经过第k个卷积核卷积运算得到的卷积结果; f(·)为激活函数; Wk为第k个卷积核的权重矩阵; x为输入特征; bk为偏置项。1D-CNN利用卷积核在时间维度方向上滑动,对时间窗口内的元素进行加权,再通过激活函数进行非线性变换来提取特征。
1.2 NGRU
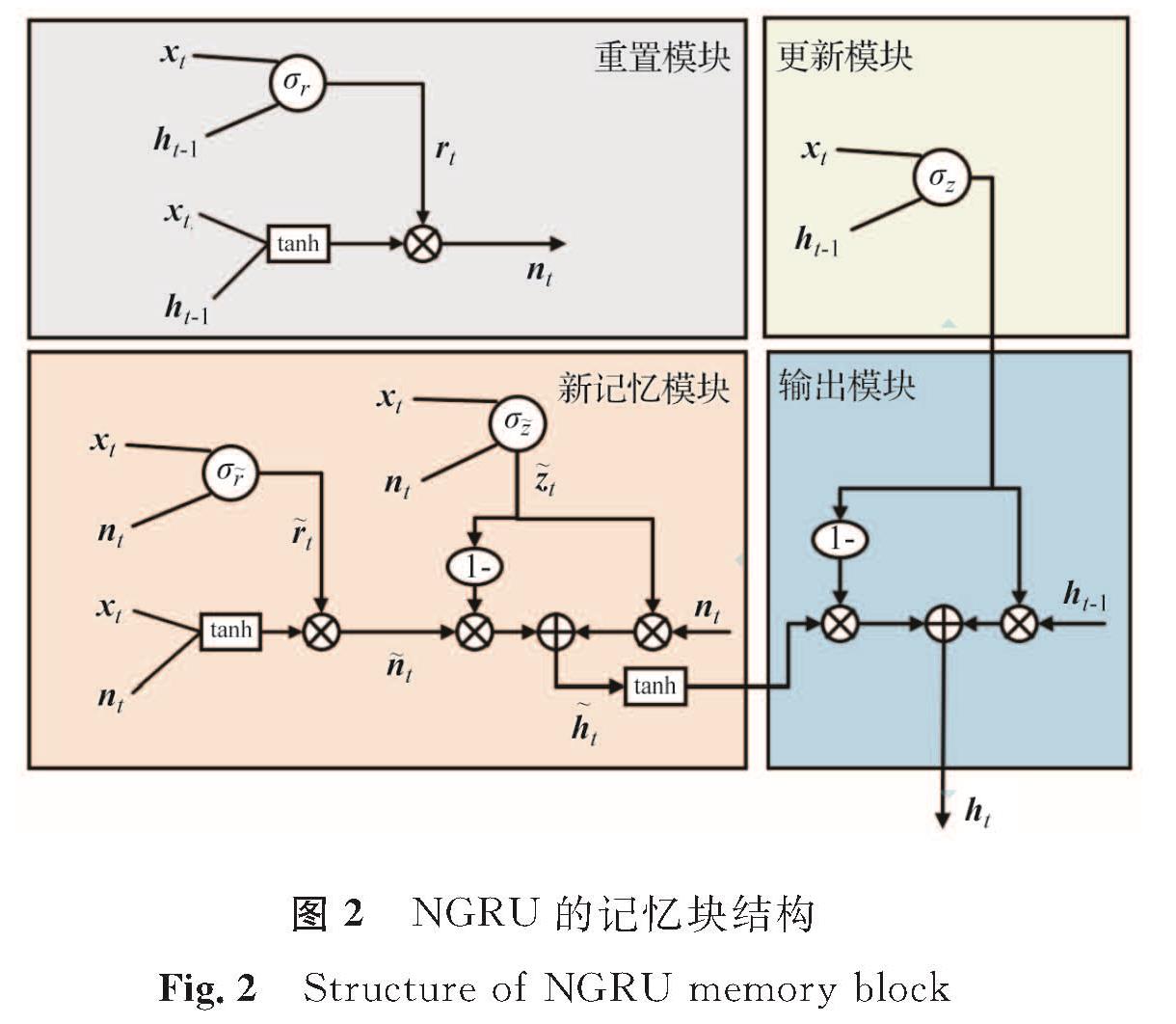
在使用循环网络对永磁同步电机进行温度预测时,为了去除相关特征中的噪声,并通过有限的特征探寻电机温度变化规律,提取更高层次的抽象的温度变化特征,本研究在GRU的基础上,采用嵌套的方式来增加模型的深度,提出一种新型循环网络并命名为NGRU。NGRU的记忆块结构如图2所示,由重置模块、更新模块、新记忆模块及输出模块组成,且NGRU仍旧保留了GRU中的重置门与更新门。在永磁同步电机的温度预测中,NGRU使用全连接层对提取的深层次特征降维,得到目标部件的预测温度。
NGRU中重置模块的作用是计算得到重置的隐藏状态,其定义如下:
rt=σr(Wr[xt,ht-1]+br) (2)
nt=rt·tanh(Wn[xt,ht-1]+bn) (3)
式(2)~(3)中:rt为重置门; σr为sigmoid激活函数; xt为当前时刻的输入; ht-1为隐藏状态; nt为重置的隐藏状态。rt与tanh(Wn[xt,ht-1]+bn)进行点乘,rt在此处起到重置的作用,决定nt包含多少xt和ht-1相关的信息。
NGRU的更新模块与常规GRU的更新门相同,其定义如下:
zt=σz(Wz[xt,ht-1]+bz) (4)
式(4)中:zt为更新门; σz为sigmoid激活函数。zt的表达式与重置模块中的重置门的表达式相似,但是线性变化的参数是不同的,因此它们具有不同的功能。
NGRU的新记忆模块用于计算得到新的记忆状态。这个模块内部包含了一个改动的GRU,将其定义为内部GRU,其定义如下:
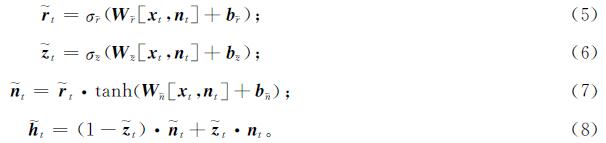
式(5)~(8)中:r~t为内部重置门; z~t为内部更新门; n~t为内部重置隐藏状态; h~t为新记忆状态; σr~、σz~为sigmoid激活函数。由重置模块得到的nt,与xt一起作为内部GRU的输入。n~t的计算不同于常规的GRU,r~t并没有与nt直接进行点乘,而是与tanh(Wn~[xt,nt]+bn~)点乘,这一步模仿了LSTM中的输出门,同时也能方便计算。在内部GRU中,通过z~t决定新记忆状态 h~t包含多少n~t与nt相关的信息。在此模块中,NGRU利用内部GRU创建了一个新的记忆层级,能更好地重构当前时刻的新记忆。
NGRU的输出模块的定义如下:
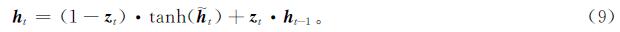
式(9)中,tanh激活函数将h~t映射到[-1,1],限制其值以便于神经网络的学习,最终通过线性差值运算得到当前时刻的隐藏状态ht。
1.3 CNGRU
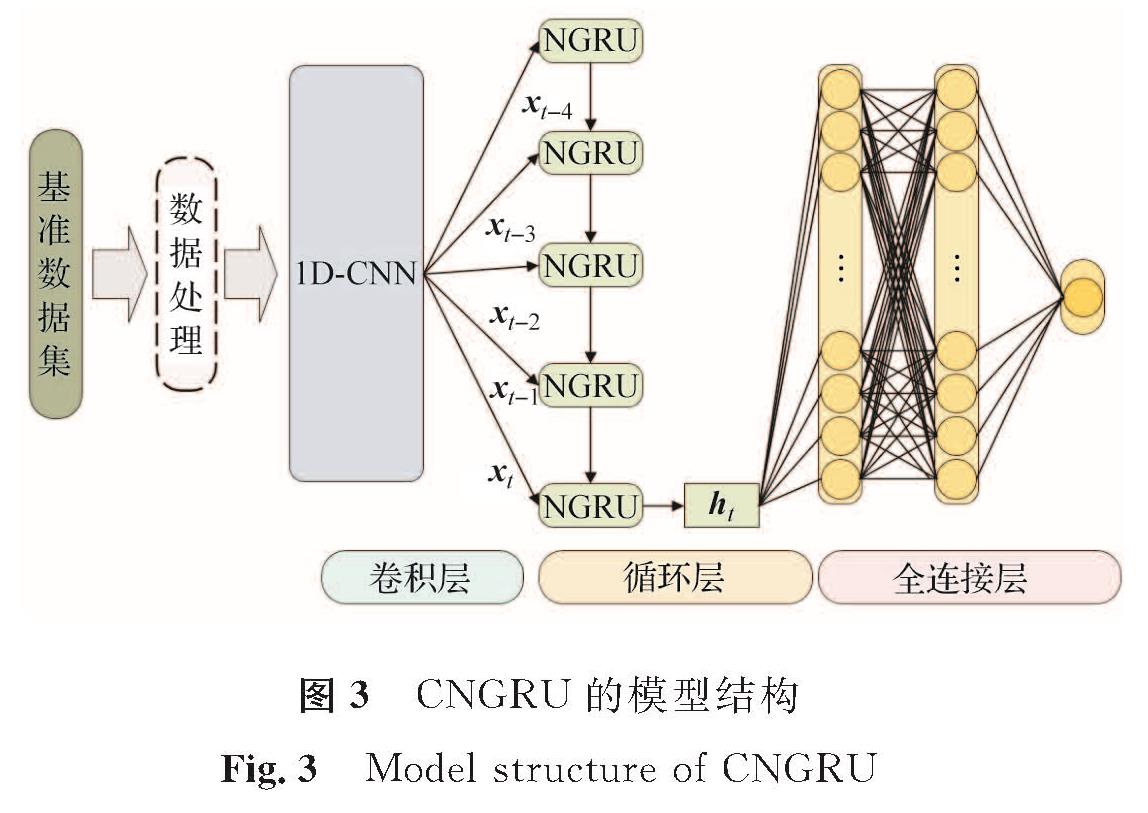
结合NGRU与1D-CNN,本研究提出了一种用于预测永磁同步电机温度的新型深度学习模型——CNGRU,模型结构如图3所示。整个模型主要分为3个部分:卷积层、循环层及全连接层。在CNGRU模型中,连续5个时刻(t-4至t)的温度相关特征被输入模型,用来预测t时刻目标部件的温度。永磁同步电机的基准数据集经过适当的处理之后,首先进入卷积层,1D-CNN进行卷积运算,从多个角度对温度变化的特征进行提取,卷积核步长为1,数量为16,相关温度特征维度将变成16维; 然后进入循环层,NGRU通过非线性变换对相关温度特征进行进一步的噪声过滤,这里的非线性变换主要依赖于NGRU模型中激活函数的作用,并且由于电机温度序列中当前温度只与当前和过去的电机状态有关,NGRU的循环网络结构能挖掘永磁同步电机温度序列在时间上的联系,从而提取更加抽象的高层次且易于神经网络计算的温度特征,经过循环层的运算,得到关于t时刻温度的相关特征; 最后经过全连接层进行降维提取,汇聚由NGRU提取的温度特征中的t时刻目标部件的预测温度。
2 试验设计2.1 数据集本试验使用的数据集来自Kaggle Data Science在线竞赛平台,由一个安装有三相永磁同步电机[16]的测试平台测得。数据的测量和收集由德国帕德伯恩大学电力电子和电气驱动系完成。数据集包含了130万余条数据,基准数据标签包括:环境温度a、冷却液温度c、电压d坐标ud、电压q坐标uq、电机转速nmech、电机扭矩Tm、电流d坐标id、电流q坐标iq、永磁体表面温度PM、定子轭温度SY、定子齿温度ST、定子绕组温度SW、唯一性标识uid。
每条数据都以2 Hz采样,唯一性标识相同的数据是在同一时间段内连续测得,并且每组标识相同的数据都可以反映永磁同步电机的整个电热特性。为节省计算资源,本研究以适当的频率对数据集进行降采样处理。由于每组标识相同的数据彼此独立,降采样操作是单独执行的,只使用相同的频率。
为了更好地预测永磁同步电机的温度,由ud、uq、id和iq衍生出以下2个特征:

式(10)~(11)中:us为d-q坐标系合成的电压值; is为d-q坐标系合成的电流值。
选取约30 000条数据作为训练集,300条数据作为测试集。定子轭、定子齿和定子绕组的温度作为永磁同步电机的温度预测目标。由于这些核心部件的温度特性不同,因此针对每个部件分别训练了CNGRU和对比模型。在温度预测中,除了预测的目标温度与唯一性标识,其余特征都被作为输入。为了使神经网络更好地进行学习,数据集进行了标准差标准化处理:
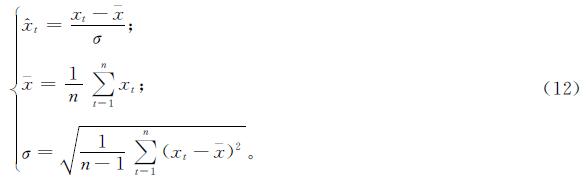
式(12)中:x^t为标准化处理后的数据; xt为t时刻的数据; x-为数据的平均值; σ为数据的标准差。
2.2 评价指标本研究引入回归任务中常用的评价指标均方误差(mean square error,MSE)yMSE、平均绝对误差(mean absolute error,MAE)yMAE及决定系数R2,分别定义如下:
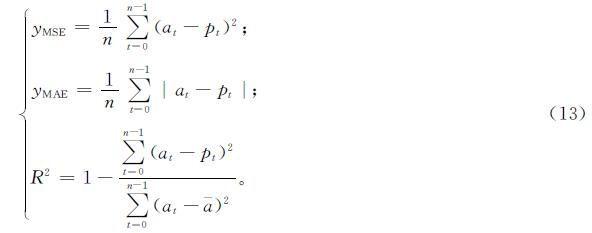
式(13)中:at、pt分别为t时刻的真实值和预测值; a-为真实值的平均值。这3个评价指标能反映模型的预测精度。
为了从其他角度评价模型表现,能反映逼近程度的L2范数和最大偏离状况的L∞范数也作为评价指标,它们能在一定程度上反映模型的稳定性,分别定义如下:

式(14)~(15)中:dt为t时刻预测值和真实值之间的差值。
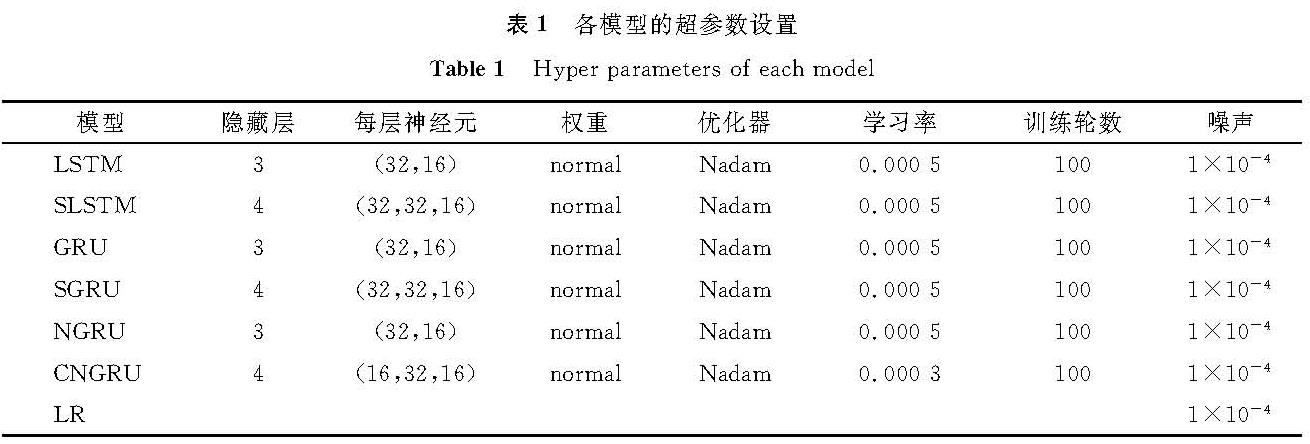
2.3 对比模型选取及参数设置本研究提出的CNGRU主要基于GRU,所以GRU被作为对比模型之一,同时LSTM也被引入进行对比。为了更好地比较本模型嵌套结构的有效性,试验中还引入了双层堆叠结构的LSTM(SLSTM)和双层堆叠结构的GRU(SGRU)作为对比模型。在此基础上,线性回归模型(linear regression,LR)也被作为对比模型。所有的深度学习模型均采用相同的时间步长5来进行永磁同步电机温度的预测。各模型的超参数设置见表1。试验硬件环境如下:CPU为i7-6700HQ,内存为16 GB; 显卡为GTX960M-2G。软件环境如下:框架库为Keras 2.2.4,Tensorflow 1.14.0; 开发环境为Pycharm 2020.3.2。
3 试验结果
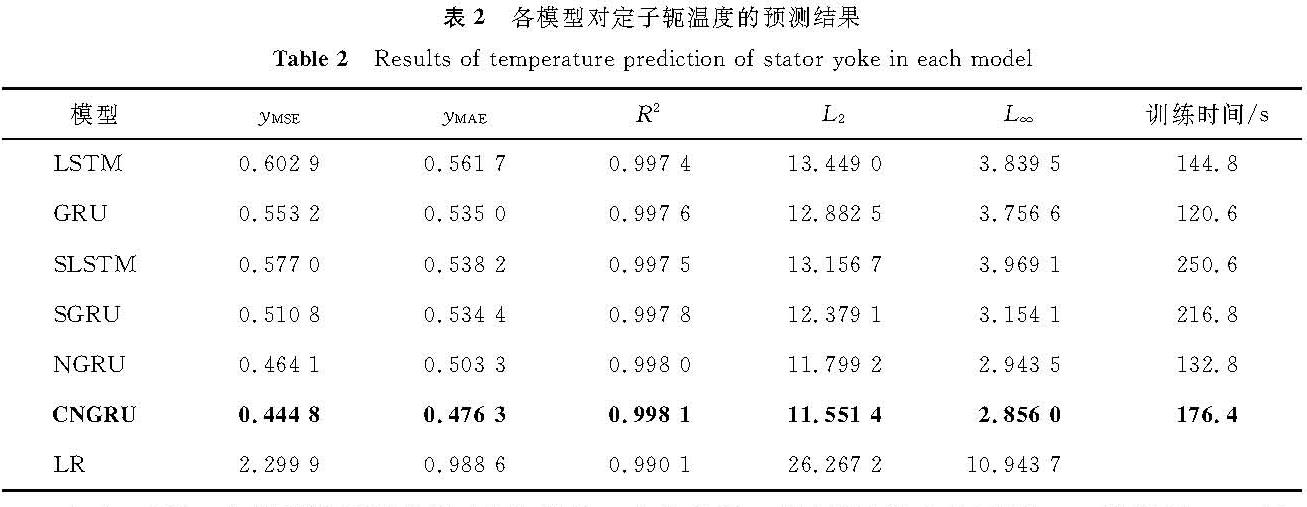
采用CNGRU、NGRU、LSTM、SLSTM、GRU、SGRU及LR模型对永磁同步电机的核心部件定子齿、定子轭及定子绕组的温度进行了预测。由于各部件温度特性存在差异,因此各目标部件温度预测的训练是分别进行的。各模型对定子轭、定子齿及定子绕组温度的预测结果见表2~4。本研究用yMSE、yMAE、R2、L2、L∞、训练时间共6个评价指标描述各模型的性能。
由表2可知,各深度学习模型相比LR都有一定的优势。SLSTM相比LSTM,yMSE降低了4.30%。SGRU和GRU相比,SGRU的yMSE也降低了7.66%。而NGRU的yMSE、yMAE值均比SLSTM和SGRU要小,yMSE分别降低了19.57%和9.14%,并且NGRU的yMSE相比GRU降低了16.11%。在定子轭的温度预测上,采用嵌套结构增加深度的NGRU表现出更强的噪声过滤能力,比其他循环网络具有更高的预测精度。CNGRU相对NGRU而言,在yMSE上降低了4.16%,而1D-CNN的引入对NGRU性能的提升效果不明显。观察各模型L∞,所有深度学习模型的L∞都明显小于LR,可见它们相对LR模型具有一定的优势。NGRU的L∞比其他循环网络平均降低0.736 3,CNGRU的L∞比其他循环网络平均降低0.823 8。这意味着在遇到电机状态改变等导致温度突变的情况时,NGRU和CNGRU相对其他对比模型具有更强的稳定性,其预测效果受到的干扰更小。
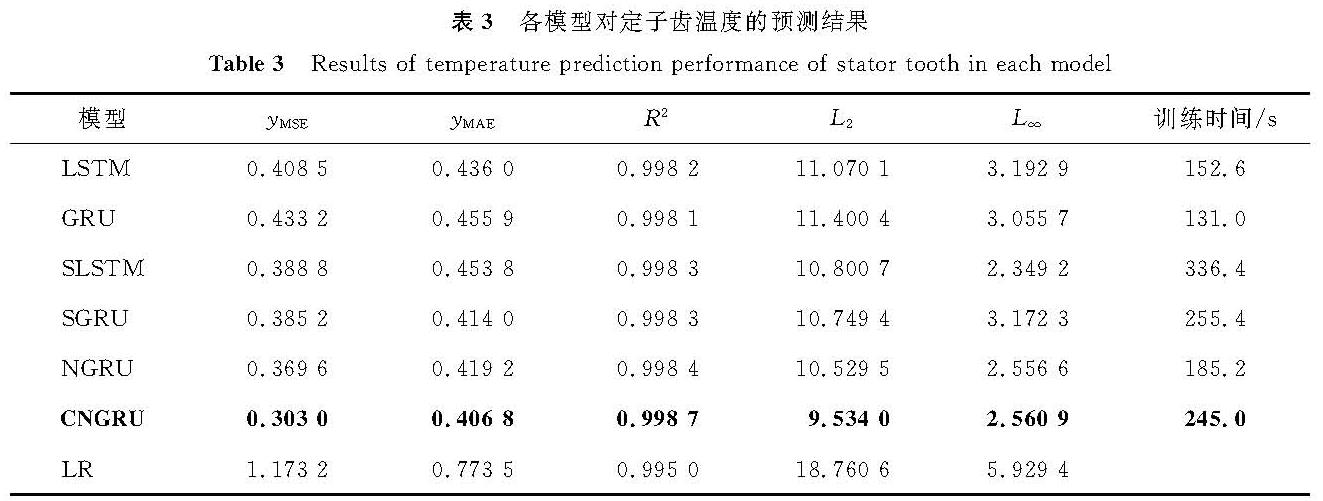
表3 各模型对定子齿温度的预测结果
Table 3 Results of temperature prediction performance of stator tooth in each model
由表3可知,NGRU比GRU的yMSE降低了14.68%,其yMSE、yMAE和L2要略优于SGRU和SLSTM,但是在L∞上略差于SLSTM。综合其余评价指标,在定子齿的温度预测中,NGRU预测的整体精度要略微优于SGRU和SLSTM。CNGRU的1D-CNN对特征的提取效果得到体现,其yMSE相比NGRU降低了18.02%。结合各模型的评价指标,定子齿的预测难度相对较小,各深度学习模型的R2都接近1,表明均达到良好的预测效果。NGRU和CNGRU相比其他循环网络,优势较小。
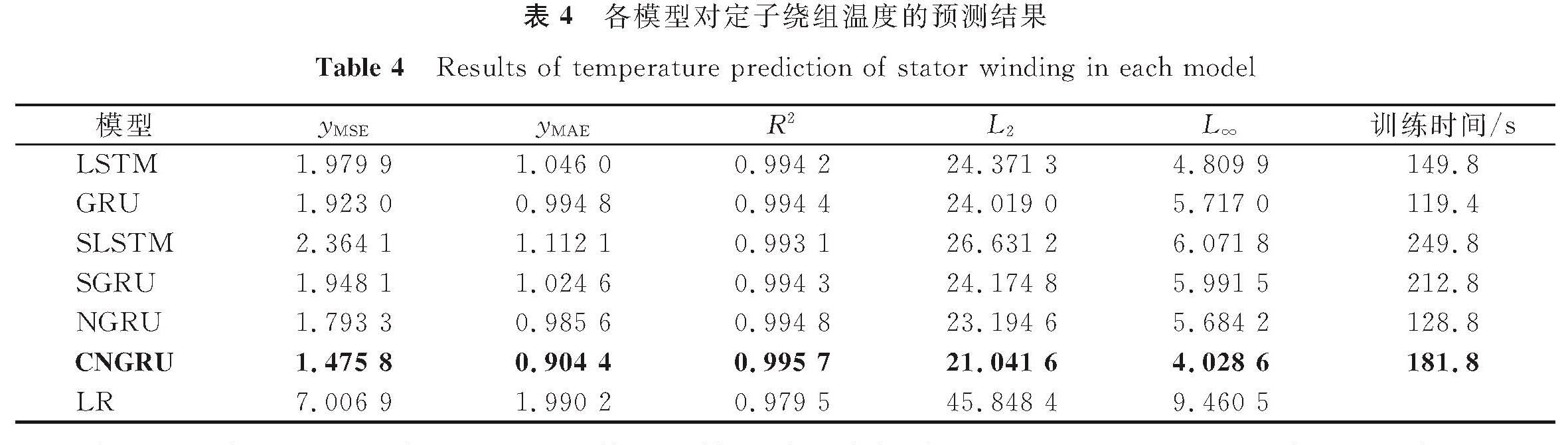
由表4可知,SLSTM相比LSTM,其预测效果并没有提升,甚至更差。而SGRU与GRU的预测表现总体上是接近的。NGRU相比SGRU和SLSTM,yMSE分别降低了7.95%和24.14%。在定子绕组的温度预测中,NGRU的嵌套结构相比SLSTM和SGRU的堆叠结构,优势明显,NGRU滤除定子绕组相关温度特征中噪声的能力更强。CNGRU相比NGRU,其yMSE降低了17.70%,L∞降低了1.655 6,1D-CNN对NGRU性能的提升得到体现。CNGRU相比其他循环网络,yMSE平均降低了27.63%,L∞平均降低了1.619 0,yMAE和R2的优势明显。对于定子绕组,CNGRU比其他模型的准确性和稳定性更高。
CNGRU和NGRU比其他循环网络具有更复杂的结构,但由表2~4可知,它们在提升预测精度的时候,并未大幅度增加训练时间,并且NGRU的嵌套结构相比堆叠结构训练时间明显减少。结合各模型对3个目标部件温度预测的表现,永磁同步电机温度预测难度由高至低依次为:定子绕组、定子轭和定子齿。对于预测难度最小的定子齿,其相关温度特征中包含的噪声较少,CNGRU和NGRU与对比模型相比并没有明显的优势,各模型都能较好地挖掘温度特征中所蕴含的信息。对于预测难度最大的定子绕组,其输入的相关温度特征中可能包含着大量的噪声。CNGRU和NGRU在预测精度上较对比模型都展现出了一定的优势,试验结果能印证NGRU具有更强的噪声过滤能力。在模型的稳定性上,NGRU要弱于LSTM,这可能是由于LSTM的细胞状态与隐藏状态相比NGRU的传递了更多有用的信息。但是CNGRU中1D-CNN的引入,进一步提升了预测效果。1D-CNN对特征多角度的提取有利于NGRU进行深层次抽象温度特征的提取,NGRU的隐藏状态能传递更加有效的信息,从而进一步提升NGRU挖掘温度序列在时间上的联系的能力。
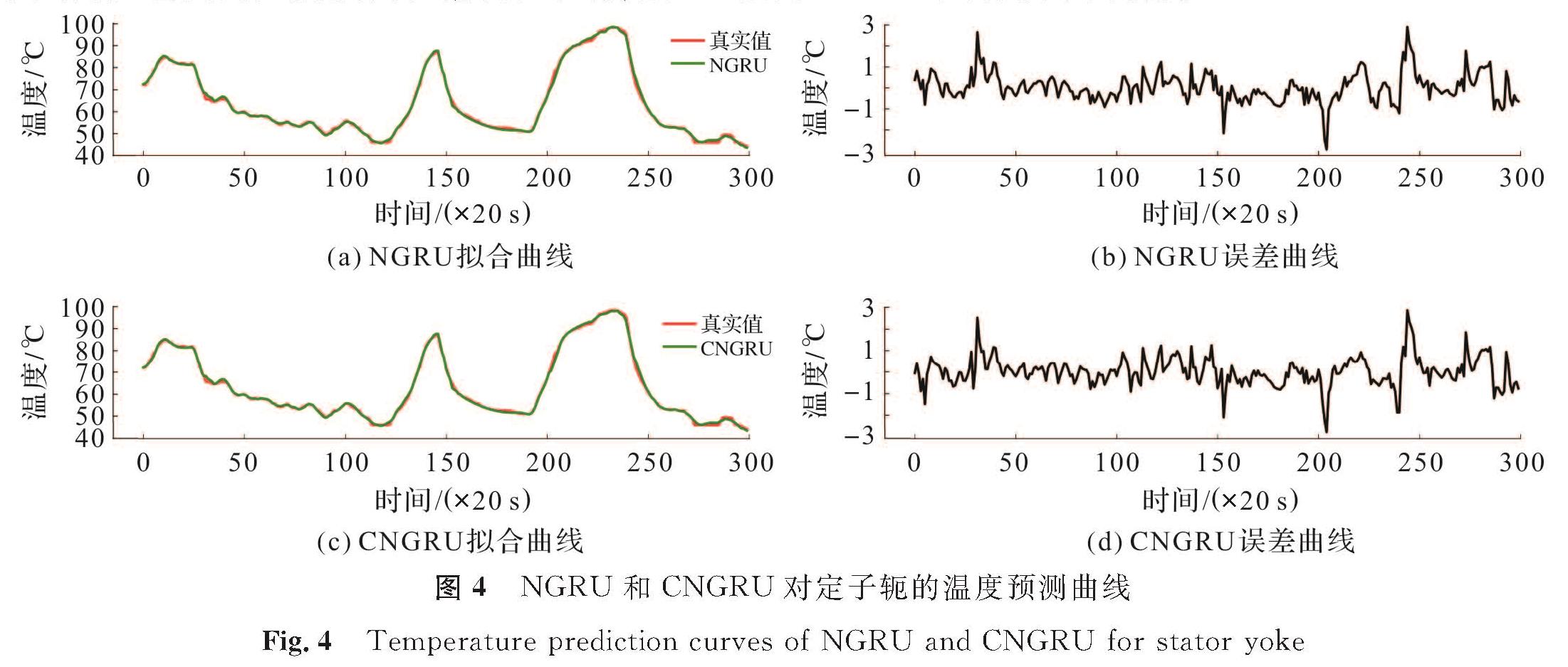
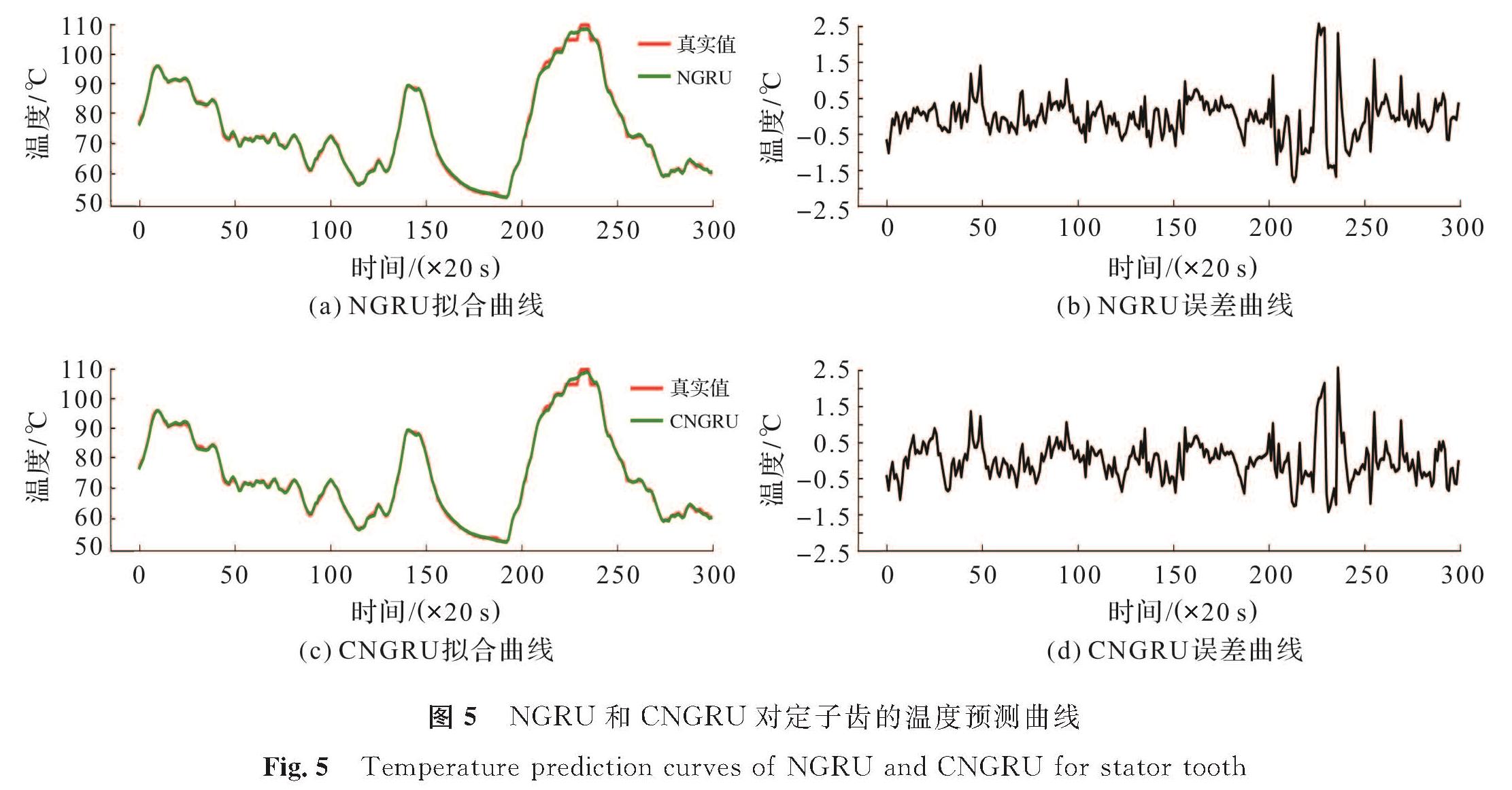
CNGRU和NGRU对比其他循环网络基本上都有着更有效与更稳定的预测能力,且CNGRU相比NGRU,yMSE平均降低了13.29%,L∞平均降低了0.579 6。CNGRU和NGRU对永磁同步电机的定子轭、定子齿和定子绕组的温度预测曲线如图4~6所示。二者对各部件温度曲线拟合良好,但对温度突变的预测精度还有待提高。对比各模型间的误差曲线,CNGRU在部分情况下略微降低了温度突变点的误差。计算各误差曲线的方差,NGRU依次为0.68、0.61和1.30,CNGRU依次为0.67、0.55和1.21。再结合表2~4中二者的拟合表现,可以得到1D-CNN的引入略微提升了CNGRU预测的稳定性,CNGRU对永磁同步电机的温度预测在精确性和稳定性上相比NGRU只有较小的优势。
4 结 语
本研究提出了一种基于GRU的新型循环网络——NGRU,将其结合1D-CNN进一步提出了一种用于永磁同步电机温度预测的深度学习模型。通过对永磁同步电机定子轭、定子齿及定子绕组的温度预测,论证了NGRU嵌套结构相比堆叠结构的有效性; 相比其他循环网络模型,NGRU和CNGRU对永磁同步电机温度预测具有一定的有效性和准确性。在此基础上,进一步对比了NGRU与CNGRU的性能差异。本研究提出的CNGRU对永磁同步电机的温度预测具有更高的精度和稳定性,能为电机的安全稳定运行提供技术保障。对循环网络在永磁同步电机温度预测上的性能比较,能为其他相关工作提供一定的参考。
- [1] 孙竟成.基于热网络法的永磁同步电机三维温度场研究[D].天津:天津大学,2016.
- [2] SI J, ZHAO S, FENG H, et al. Analysis of temperature field for a surface-mounted and interior permanent magnet synchronous motor adopting magnetic-thermal coupling method[J].CES Transactions on Electrical Machines and Systems,2018,2(1):166.
- [3] FANG J, DING S, SUN Y, et al. Signal injection method without torque ripple for stator winding temperature estimation of surface-mounted PMSM drive systems[J].Journal of Power Electronics,2020,20(6):1504.
- [4] 丁树业,朱敏,江欣.永磁同步电机三维全域温度场与温度应力耦合研究[J].电机与控制学报,2018,22(1):53.
- [5] 刘平,王鑫,孙千志,等.永磁同步电机定子绕组温度估计的信号注入策略优化[J].电机与控制学报,2019,23(11):18.
- [6] 丁树业,江欣,朱敏,等.基于集总参数热网络法的永磁同步电机启动及稳态温升分析[J].电机与控制学报,2020,24(5):143.
- [7] BALAMURALI A, KUNDU A, CLANDFIELD W, et al. Non-invasive parameter and loss determination in PMSM consideringthe effects of saturation, cross-saturation, time harmonics and temperature variations[J].IEEE Transactions on Magnetics,2021,57(2):340.
- [8] WALLSCHEID O, KIRCHGÄSSNER W, BÖCKER J. Investigation of long short-term memory networks to temperature prediction for permanent magnet synchronous motors[C]//2017 International Joint Conference on Neural Networks(IJCNN). Anchorage:IEEE,2017:1940.
- [9] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J].Neural Computation,1997,9(8):1735.
- [10] KIRCHGÄSSNER W, WALLSCHEID O,BÖCKER J. Deep residual convolutional and recurrent neural networks for temperature estimation in permanent magnet synchronous motors[C]//2019 IEEE International Electric Machines & Drives Conference(IEMDC). Santiago:IEEE,2019:1439.
- [11] GUO H, DING Q, SONGY, et al. Predicting temperature of permanent magnet synchronous motor based on deep neural network[J].Energies,2020,13(18):4782.
- [12] WANG X F, ZHANG Y. Multi-step-ahead time series prediction method with stacking LSTM neural network[C]//2020 3rd International Conference on Artificial Intelligence and Big Data(ICAIBD). Chengdu:IEEE,2020:51.
- [13] WANG X, XU L, CHEN K. Data-driven short-term forecasting for urban road network traffic based on data processing and LSTM-RNN[J].Arabian Journal for Science and Engineering,2019,44(4):3043.
- [14] CHUNG J, GULCEHRE C, CHO K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL].(2014-12-19)[2021-06-10].https://arxiv.org/abs/1412.3555.
- [15] KIRANYAZ S, AVCI O, ABDELJABER O, et al. 1D convolutional neural networks and applications:a survey[J].Mechanical Systems and Signal Processing,2021,151:107398.
- [16] WALLSCHEID O, BÖCKER J. Global identification of a low-order lumped-parameter thermal network for permanent magnet synchronous motors[J].IEEE Transactions on Energy Conversion,2015,31(1):354.
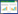 图 1 1D-CNN的基本工作原理
Fig.1 Fundamental working principle of 1D-CNN
图 1 1D-CNN的基本工作原理
Fig.1 Fundamental working principle of 1D-CNN