在高速列车场景下,自由空间光(free space optical,FSO)通信技术使用激光作为载体,具有不受多普勒频移影响,抗干扰、带宽大[1-2]等优点,可以为高速列车乘客提供高质量网络。虽然FSO通信技术具有很多优势,但是将其应用在高速列车上也面临一些困难,如高速列车运行时的振动对车体的建模、激光的发射与接收等有着不可忽视的影响。Paudel等[3]建立了一种包含地上和地下两种形式的高速列车FSO通信模型,仿真结果表明,模型中基站覆盖范围达到75 m,在误码率为10-6下传输速率达到10 Mb/s。Mohan等[4]设计了分布式多波束覆盖模型,减少了基站切换带来的影响,优化了通信链路。Akella等[5]设计了一种可以自动校准激光收发机的模块,解决了视距线和通信天线之间对准的问题。Fathi-Kazerooni等[6]提出了2种不同的FSO覆盖模型,找到了从列车轨道到地面基站、无缝连接的基站之间的最佳距离。Fan等[7]建立了一种具有双收发机的高速铁路场景下FSO通信系统模型,并分析了该模型最小覆盖点的发散角和距离对接收功率沿轨迹的影响,得到了该模型单个基站的收发机的最大总覆盖长度。文献[3-7]建立的模型未考虑列车在高速运行时的振动对激光收发机的影响,列车的振动会影响激光收发机的对准,进而会影响激光信号在激光收发机间的传输,严重时可使通信链路中断。由于高速列车在运行时振动会影响车体顶部与基站激光收发机间的相互对准,进而影响通信系统的性能,所以将FSO通信技术应用在高速列车上就必须考虑高速列车车体的振动对FSO通信系统的影响。陈春俊等[8]设计了多目标约束下的混合半主动控制算法,改善了列车横向平稳性。许文天等[9]提出了一种模糊天棚阻尼控制方法,建立一个动车组横向半主动悬挂控制模型,仿真结果表明该方法能有效提升动车组横向动力学水平。Kang等[10]对高速列车横向动力学进行了研究,分析了从0.53 Hz到39.77 Hz车体滚动、轮对偏航等13种振动模式。缪慧敏[11]15建立了1/4车体四自由度垂向振动模型,利用车体垂向位移与轨道高低不平顺之间的传递函数来搭建车体的Simulink仿真模型,获得了车体的垂向位移,并分析了垂向位移对FSO通信链路中指向性误差的影响。高速列车的振动主要有垂向和横向上的振动,文献[8-11]建立的模型对车体的振动考虑不全,其中文献[8-10]建立了高铁列车横向振动模型,未将垂向上的振动加入模型中; 文献[11]在其建立的高铁车体垂向振动模型基础上,研究了车体垂向位移对FSO通信链路中指向性误差的影响。
针对上述文献对车体横向振动影响下高铁FSO通信链路指向误差的研究不足,本研究将使用TB/T 3352—2014 《高速铁路无砟轨道不平顺谱》[12]中的轨向、轨距不平顺功率谱推导横向合成不平顺谱公式,利用横向合成不平顺谱生成横向合成不平顺数据。在此基础上建立车体振动模型仿真获取车体横向位移,对其进行验证并做统计特性分析,研究车体横向位移对FSO通信链路中指向性误差的影响。
1 轨道横向合成不平顺数据在常见的车地FSO通信链路中,在轨道旁平行于轨道间隔分布基站,且基站顶部安装激光发射机。车体顶部安装接收机,在高铁运行中收发机需要保持对准。图1是车地间的FSO通信链路模型,z为激光收发机间的距离。
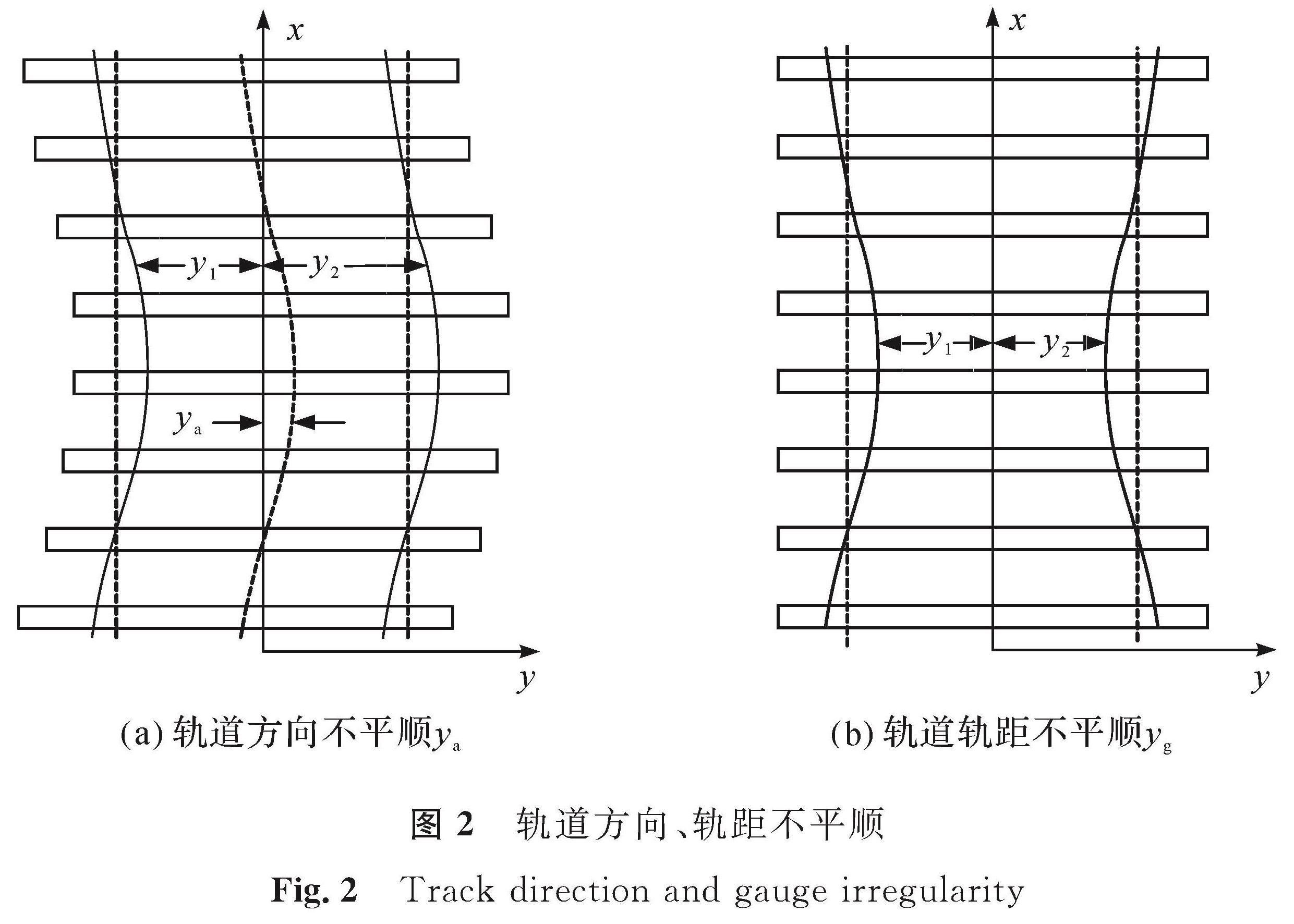
一般情况下轨道不平顺指两股钢轨的实际尺寸与理想平顺状态的偏差[13]113。轨道横向上常见的不平顺有轨道方向、轨距不平顺两种,如图2所示。
图2(a)中,轨道方向不平顺ya为实际轨道中心线相对理论轨道中心线的偏差,即
ya=(y1+y2)/2。(1)
式(1)中:y1为左轨道的横向坐标值,在图2中y1为负值; y2为右轨道的横向坐标值。
图2(b)中,轨距不平顺yg为实际轨距与名义轨距之差,即
yg=y2-y1-G。(2)
式(2)中:G为轨道名义轨距[14]。
为研究轨道方向不平顺ya、轨距不平顺yg对车体横向随机振动的影响,将二者进行叠加,得到横向合成不平顺
yh=ya+(yg)/2。(3)
影响轨道不平顺的因素很多,轨道不平顺呈随机性,是一个复杂的随机过程。为描述轨道不平顺,常用功率谱密度函数(power spectral density,PSD)来表征轨道随机不平顺[15]。横向合成不平顺谱Syh可由横向合成不平顺的自相关函数做傅里叶变换[16]得到,即

根据自相关函数定义[17]可知,RXX(t,t+τ)=E[X(t)X(t+τ)],将其代入式(4),可得
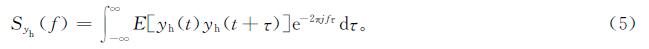
将式(3)代入式(5)整理可得
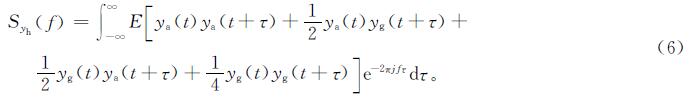
由随机变量数学期望的性质可知

假设ya(t)和yg(t)是相互独立的随机过程,且E[ya(t)]=0,可得
E[ya(t)yg(t)]=E[ya(t)]E[yg(t)]=0。(8)
将式(8)代入式(7)整理可得

再将式(5)代入式(9)可得横向合成不平顺的功率谱

根据TB/T 3352—2014 《高速铁路无砟轨道不平顺谱》,其中高速铁路无砟轨道轨向、轨距不平顺功率谱[12]
S(F)=A/(Fn)。(11)
式(11)中:F为空间频率; A和n分别为轨向、轨距拟合系数。为方便计算,对式(10)中的功率谱进行单位换算。利用Sf(f)df=SF(F)dF,f=Fv,可得
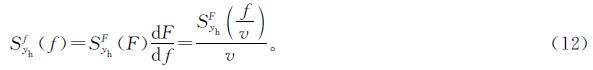
将式(11)代入式(12),可得

式(13)中:Aya、nya均为《高速铁路无砟轨道不平顺谱》中轨向不平顺的拟合系数。

式(14)中:Ayg、nyg均为《高速铁路无砟轨道不平顺谱》中轨距不平顺的拟合系数。再将式(13)、式(14)代入式(10)中可得
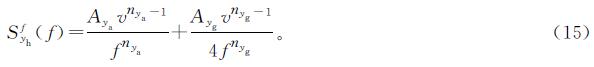
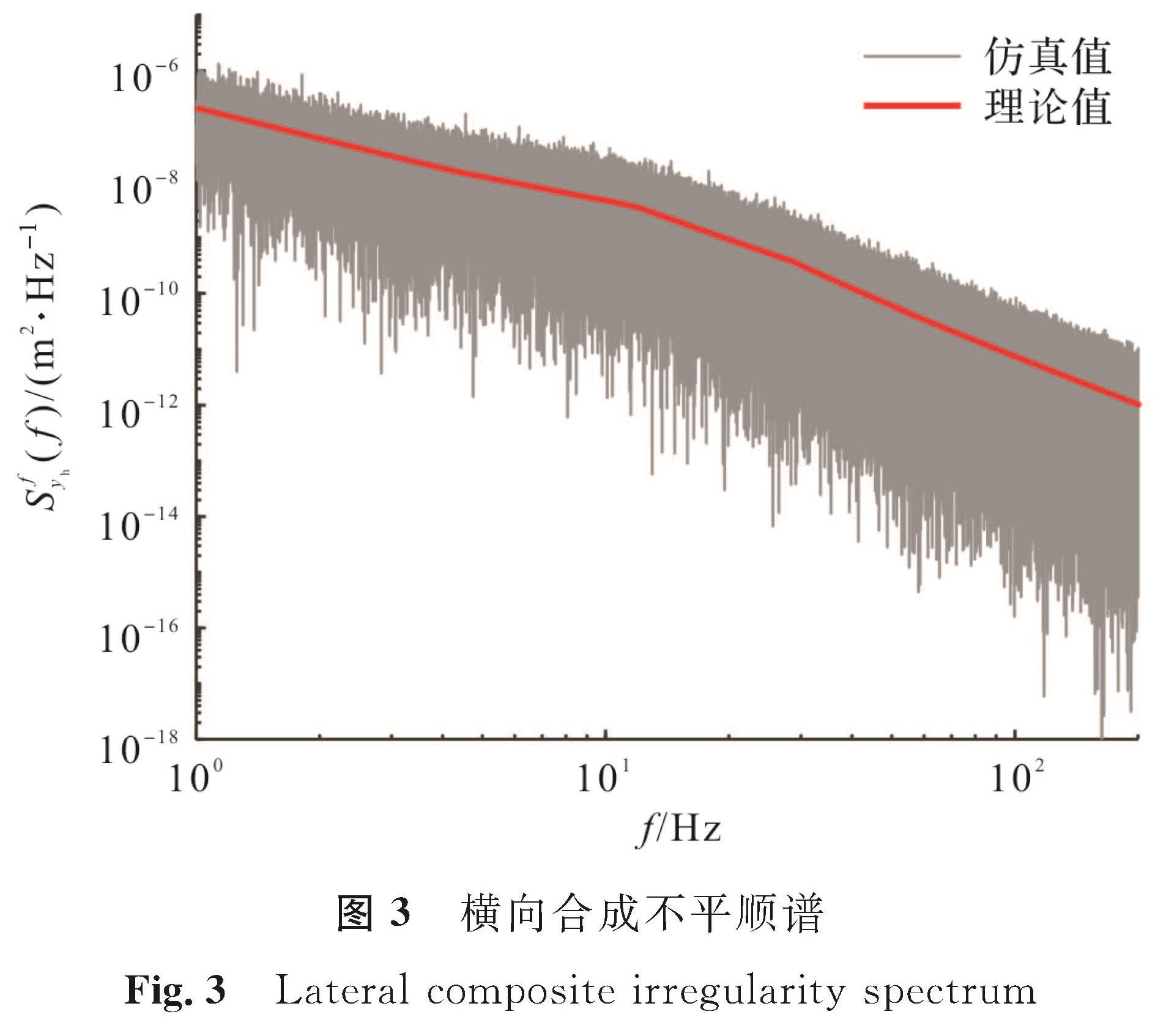
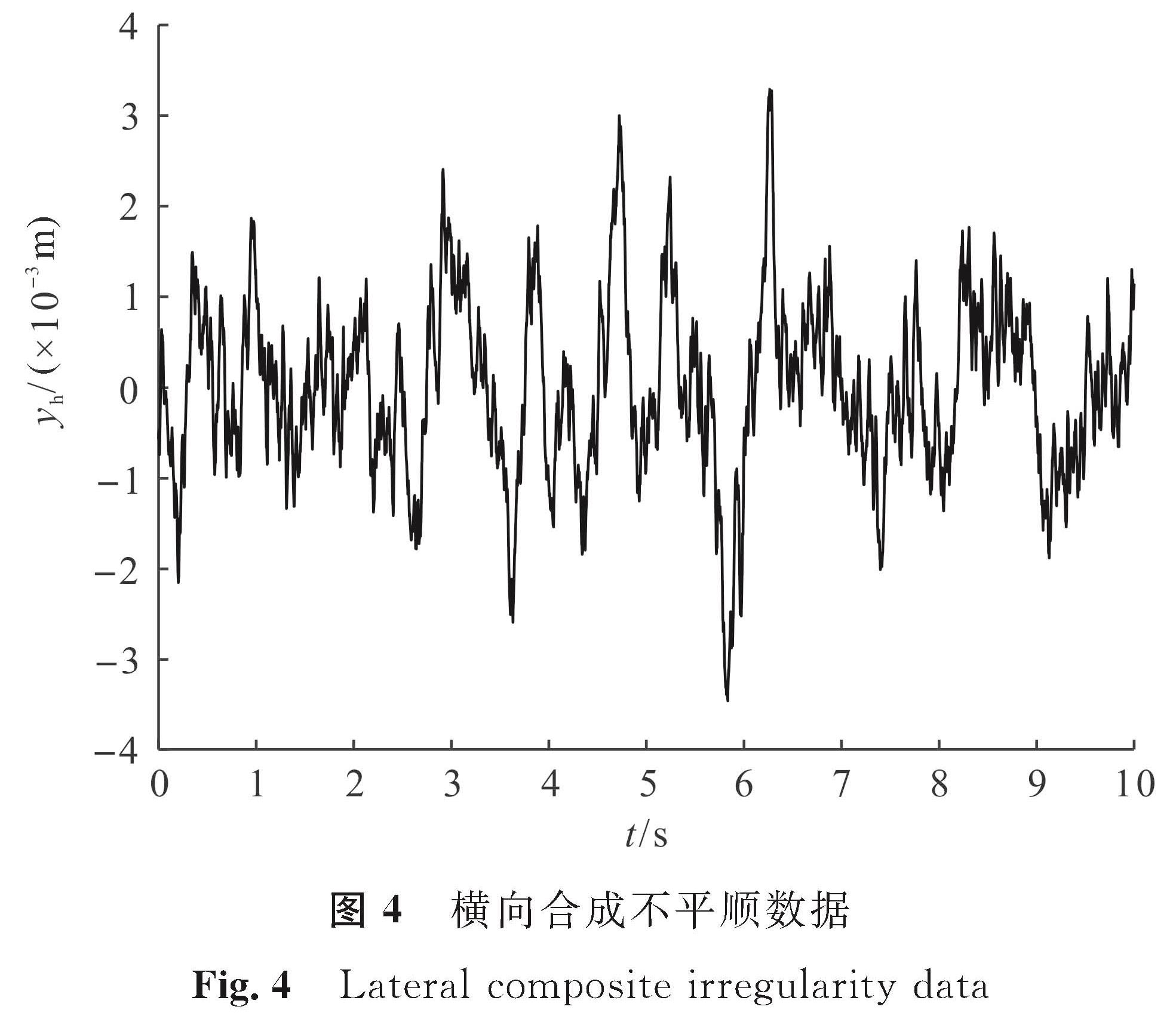
利用式(10)计算中国高速无砟轨道横向合成不平顺的功率谱密度函数理论值。利用逆傅里叶变换法[13]128及式(15)给出的关系式,在v=350 km/h下仿真可得横向合成不平顺功率谱密度和横向合成不平顺数据。图3是横向合成不平顺谱,从中可以看出横向合成不平顺谱的理论值与仿真值相吻合。横向合成不平顺数据如图4所示。
2 车体横向位移
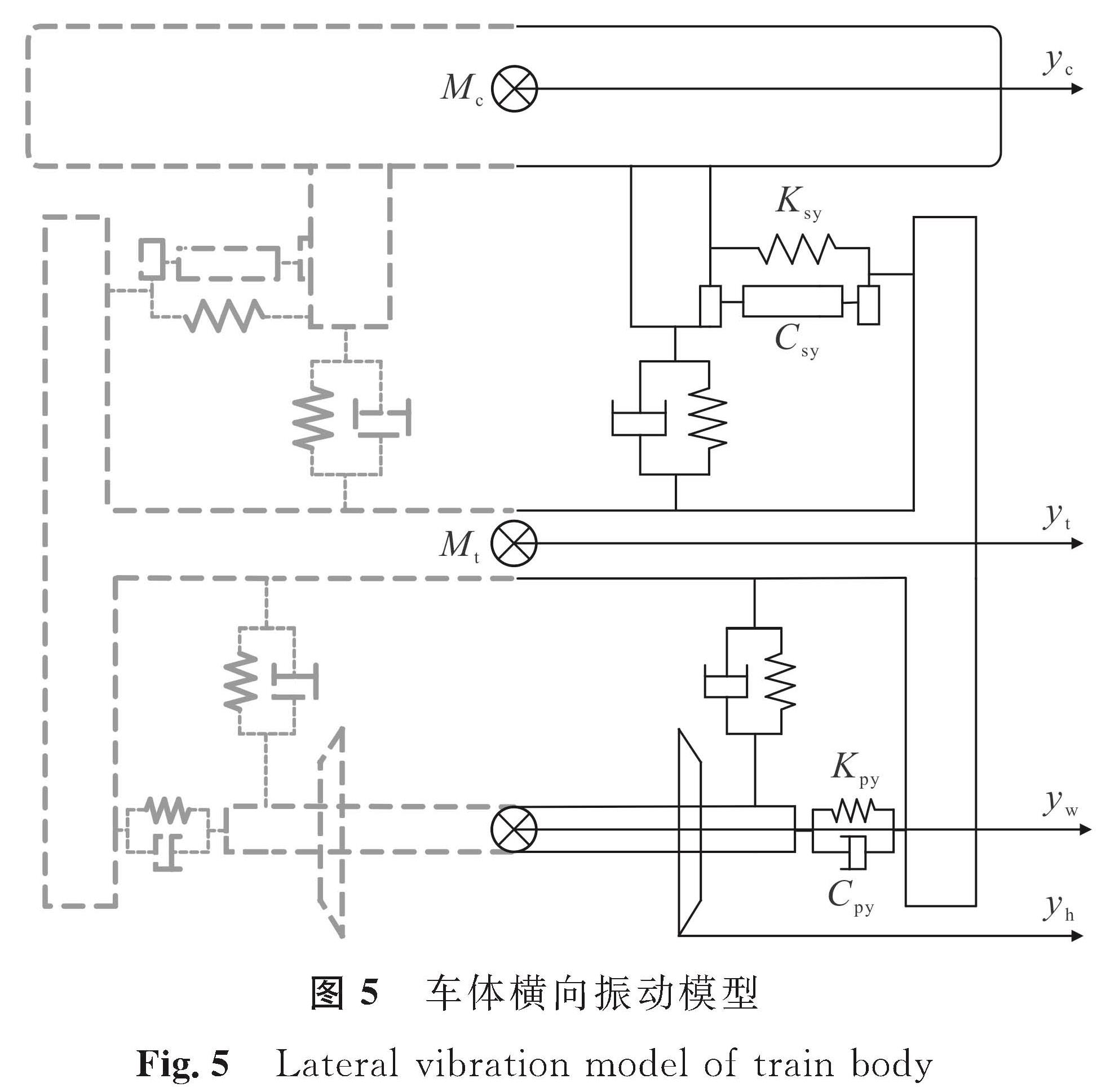
为研究车体横向位移,建立了一个3自由度1/4车体横向振动模型,如图5所示。忽略轮轨的蠕滑力关系,轮子视为刚体,只考虑轨向和轨距不平顺引起前后轮构架和车体的横向移动、构架和车体横移。图5中Mc为车体质量; Mt为一台转向架构架的质量; Kpy为一系悬挂每轴箱横向弹簧刚度; Cpy为一系悬挂每轴箱横向阻尼系数; Ksy为二系悬挂每侧横向悬挂刚度; Csy0为二系悬挂每侧横向阻尼的最小值; Csy为二系悬挂每侧可调减振器的值(除去最小值Csy0的部分); yc为车体的横向振动位移; yt为悬挂的横向振动位移; yw为轮对中心的横向位移,因为忽略轮轨的蠕滑力,yw与横向合成不平顺yh相等。模型微分方程[18]35如下:

式(16)中:Csy0=20 000 N/m; Csy=20 000 N/m; 其余参数数值见文献[18]232-233。
根据式(16)车体横向振动微分方程,对式(16)做拉普拉斯变换,可得车体横向振动微分方程的拉普拉斯变换形式,整理后如下:
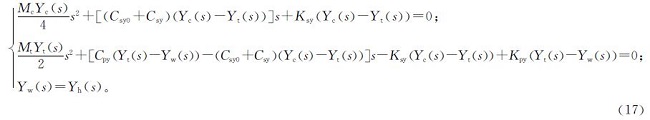
传递函数指线性系统输出y(t)的拉普拉斯变换Y(s)与输入x(t)的拉普拉斯变换X(s)之比,记作H(s),即
H(s)=(Y(s))/(X(s))。
对经过拉普拉斯变换的式(17)求解,可得车体横向位移yc与横向合成不平顺yh之间的传递函数

式(18)中:

利用式(18)和Simulink中的传递函数模块搭建车体横向振动仿真模型,如图6所示。
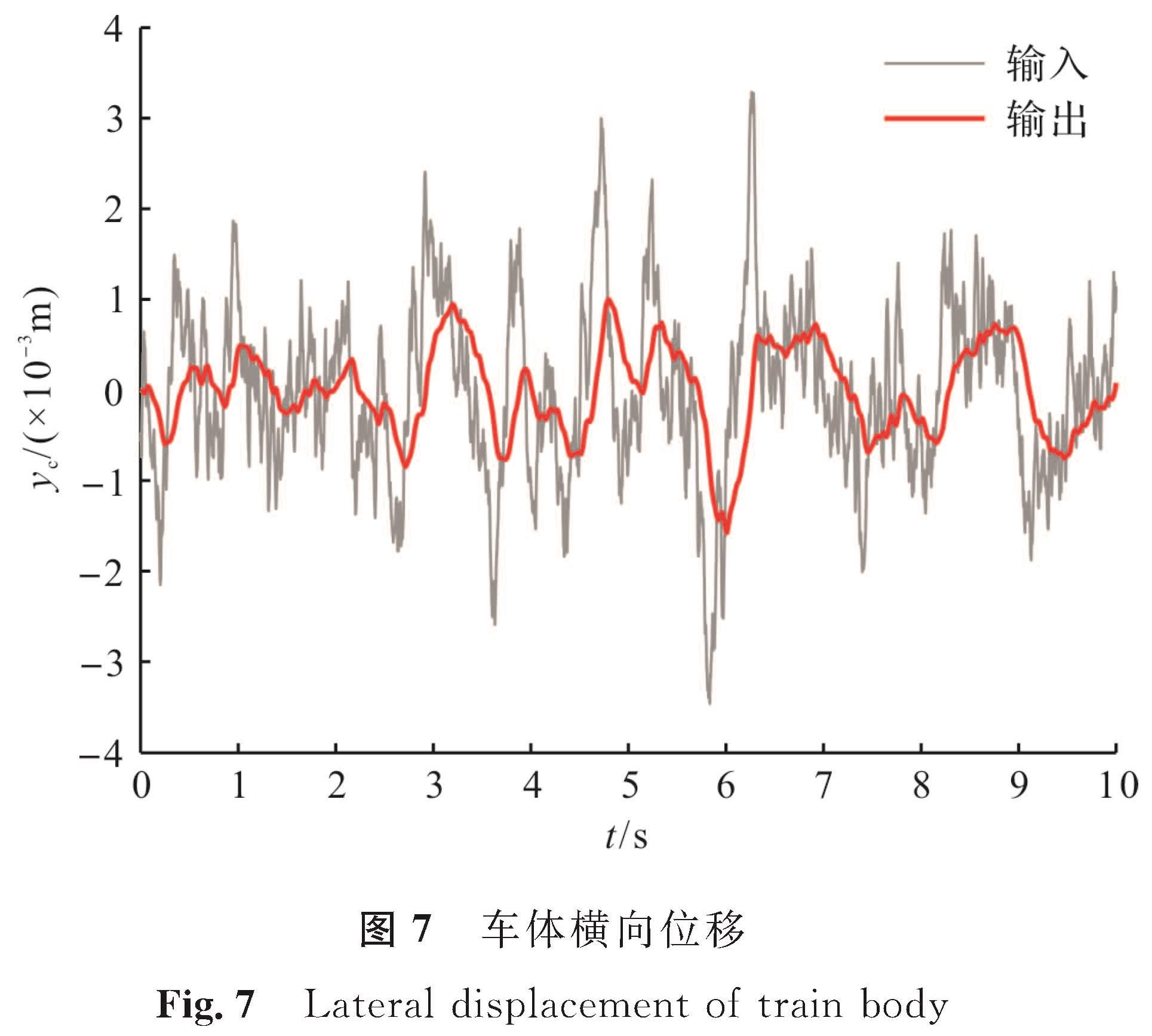
在Simulink仿真模型中,将传递函数的参数写入传递函数模块,使用生成的中国高速无砟轨道横向合成不平顺时域数据作为车体横向振动模型仿真的输入数据,在速度为350 km/h、采样间隔为10-4 s、采样点数为225条件下,仿真即可得车体的横向振动位移yc,如图7所示。由图7可以看出经过车体悬架的减振,车体的横向位移yc明显小于输入的轨道横向合成不平顺yh。
通过式(18)车体横向位移yc与横向合成不平顺yh之间的传递函数,可推导出车体横向位移yc的功率谱密度函数。利用拉普拉斯变换与傅里叶变换的换算关系s=jω,又ω=2πf,可得s=2πjf,便可将H(s)改为H(ω)。Yc(ω)与Yh(s)之间的传递函数
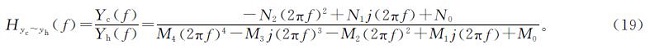
又由输入信号功率谱密度SX(f)和输出信号功率谱密度SY(f)的关系[19]为SY(f)=SX(f)|H(f)|2,则可得车体横向位移的功率谱密度函数
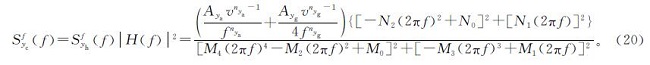
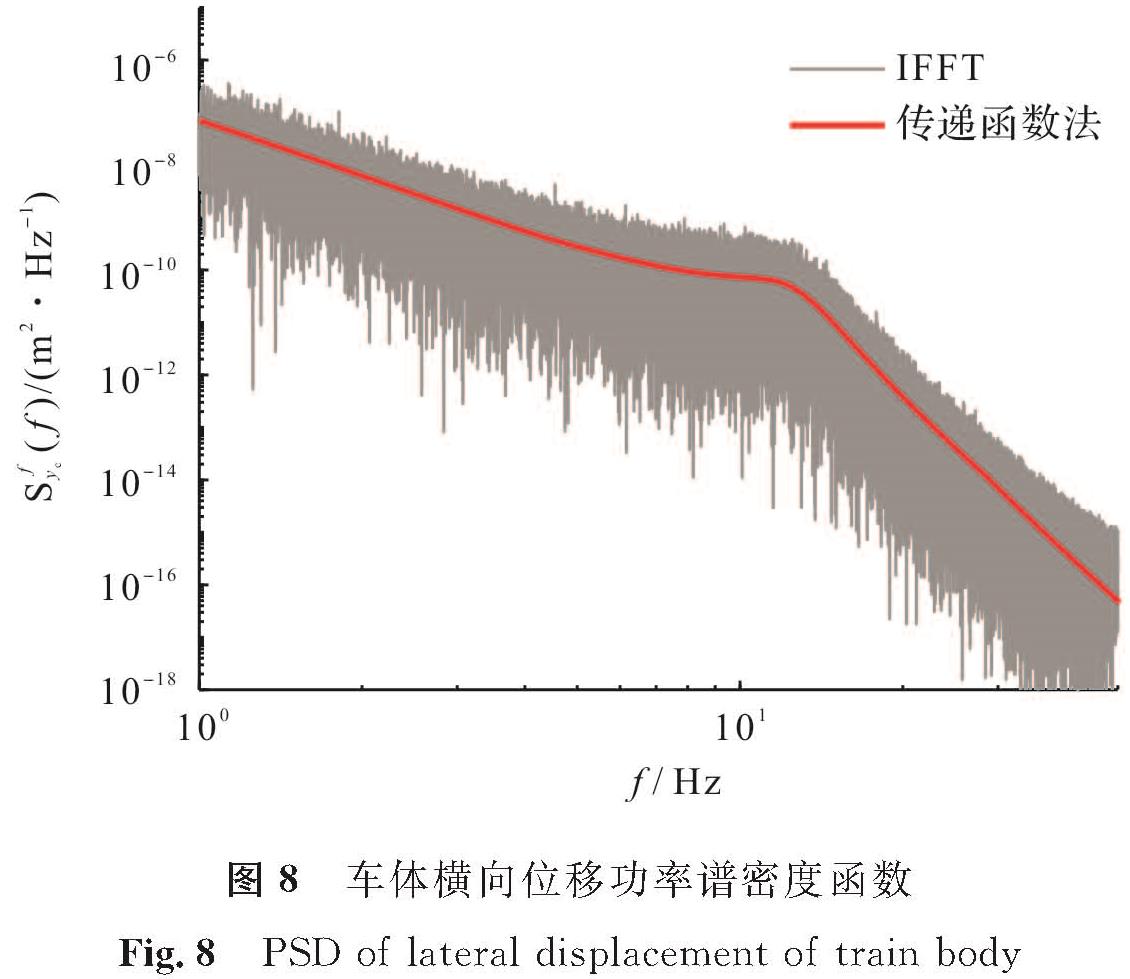
利用式(20)计算出车体横向位移yc功率谱密度的理论函数,再利用傅里叶变换求出仿真得到的车体横向位移功率谱密度函数,如图8所示,从中可以看出理论曲线与仿真曲线相吻合。
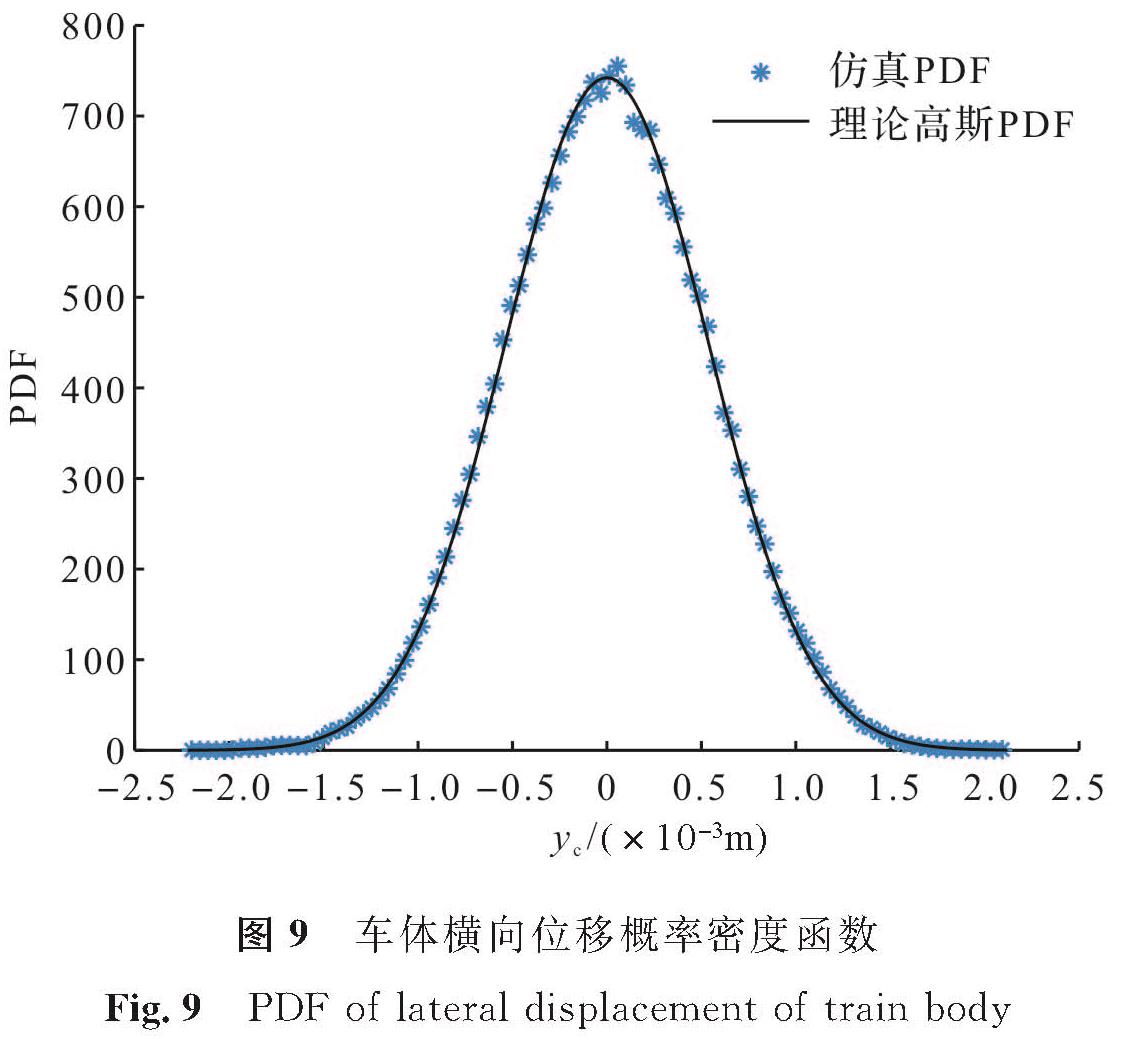
由于轨道不平顺具有随机性,则车体横向位移也具有随机性。从概率论的角度来看,车体横向位移是一离散型随机变量,其均值和方差可按照离散型随机变量来计算。使用仿真得到的车体横向位移数据来计算,可得其均值估计量(^overμ)yc=-3.72×10-8,方差估计量(^overσ)2yc=2.91×10-7。由此可以认为yc服从均值为0、方差为2.91×10-7的高斯分布,概率密度函数
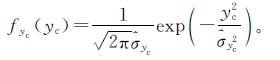
将其与具有相同均值和方差的高斯分布函数做对比,如图9所示,从中可以看出两者相吻合。
3 FSO通信横向指向性误差
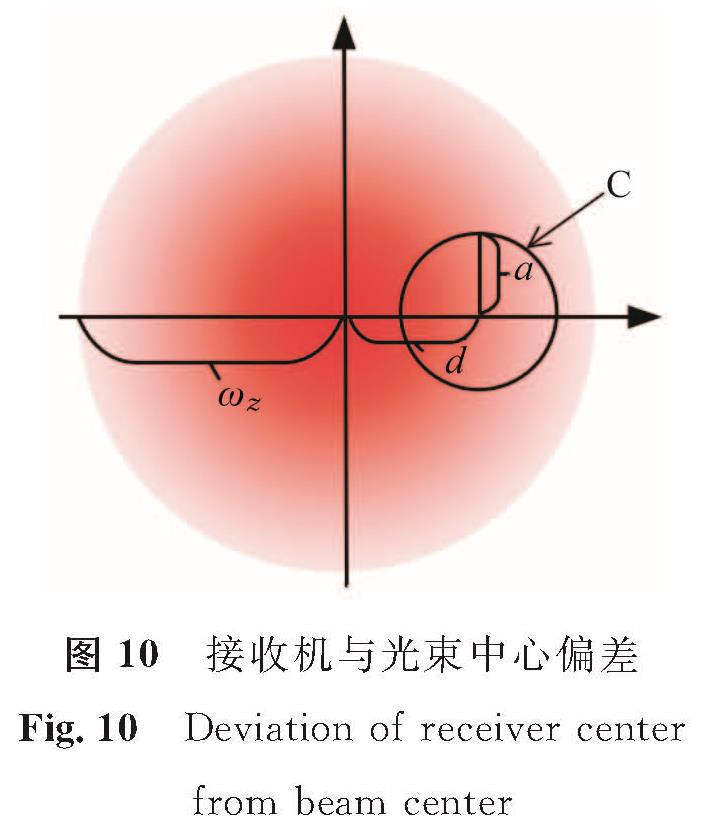
在利用式(18)仿真得到车体横向位移的基础上,我们研究高铁激光收发机间的指向性误差。图 10为激光光束照射到接收机上,接收机与光束中心偏差的示意图。以接收机上的激光束的中心为原点建立坐标系,红色圆圈是发射机发射出的激光束,接收机C是以a为半径的圆形透镜。由于车体存在随机的横向振动,造成安装在车体上的接收机左右横向振动,使发射机所发出的激光束中心和接收机中心之间产生横向偏差位移d,进而使收发机中心不能对准,产生指向性误差hp。
本文仅研究车体的横向振动对通信链路造成的指向性误差,故可将车体横向位移视作激光光束的横向偏差,即d=yc。接收机C所能收集到的光斑功率与光斑总功率的比值即指向性误差。为了便于计算,将hp表示为Marcum Q函数的形式[20]:

式(21)中:QMar是一阶Marcum Q函数; ωz是光束强度在距离中心点下降e-2时的半径值。这种形式可以近似为高斯分布形式[21]:
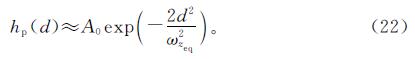
式(22)中:A0为接收到的光束功率在横向偏差d=0时的部分,A0=[erf(υ)]2; ωzeq为等效光束宽度,

式(23)中:
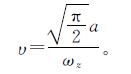
若已知随机变量x的概率密度函数,则可利用y=g(x)关系式来确定的y概率密度函数。解方程y=g(x),xn为实根,则有y的概率密度函数[22]
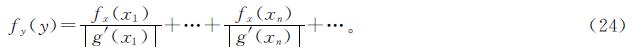
式(24)中:g'(x)为g(x)的导数。可利用式(23)推导出hp的概率密度函数[11]41-42

式(25)中:
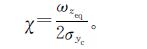
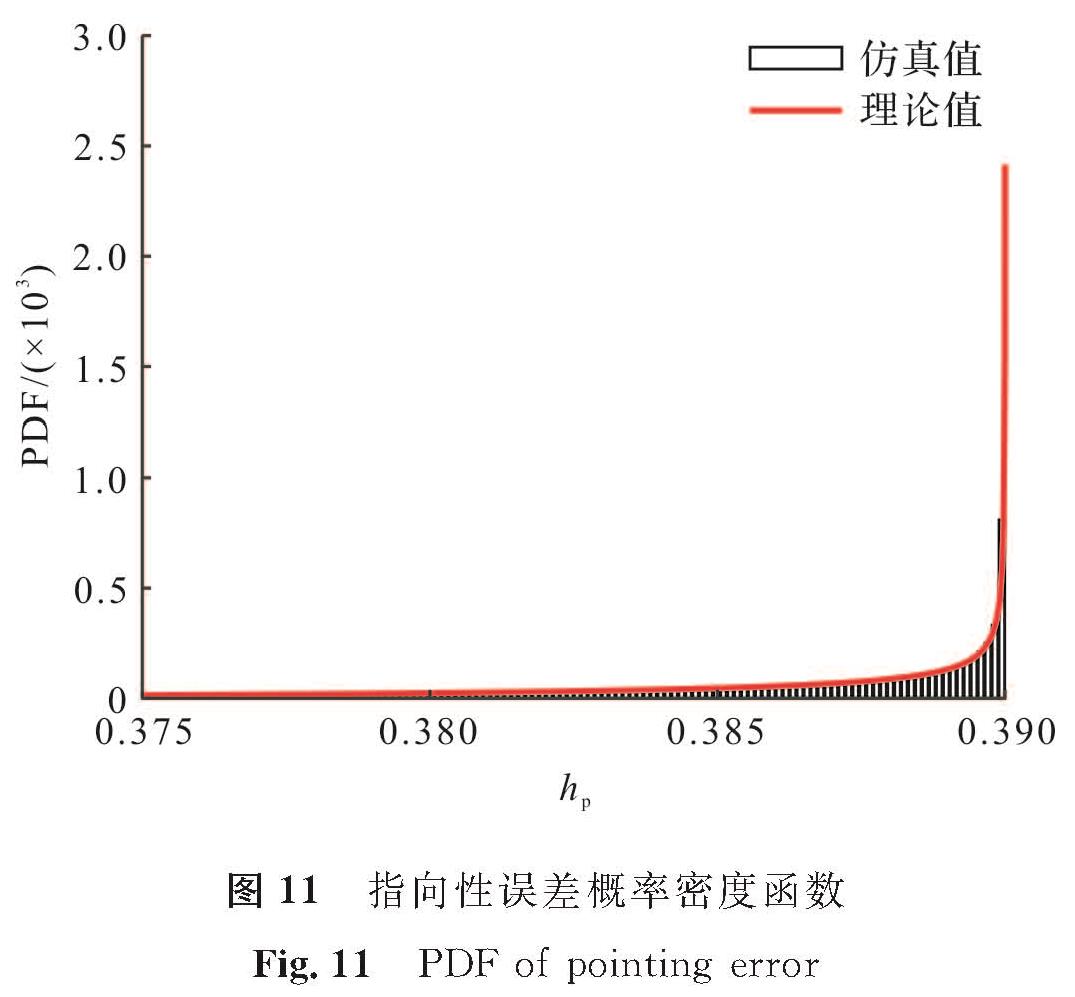
根据式(25)可画出hp的PDF理论值,即图 11中红色理论值曲线。用蒙特卡洛仿真随机生成yc,根据式(22)计算可得hp,利用直方图法统计hp的PDF,得其仿真值。指向性误差概率密度函数如图 11所示。从图 11中可知,理论值和仿真值相吻合。
4 结 语
本研究探讨了车体横向振动对高铁FSO通信指向性误差的影响,推导出了中国高速铁路无砟轨道横向合成不平顺谱公式。利用车体模型的传递函数仿真得到车体横向位移,大约在-1~1 mm,推导并仿真了其功率谱,验证其概率密度函数呈高斯分布。仿真验证车体在横向位移影响下高铁FSO通信指向性误差的概率密度函数,该指向性误差的概率密度函数将用于后续FSO通信链路信道模型的建立、性能分析和仿真。轨道水平不平顺也可以造成一定的横向、垂向振动,下一步将轨道水平不平顺加入模型并将车体横向、垂向振动融合并建模,以仿真分析其对高铁FSO通信指向性误差的影响。
- [1] FAN Q, TAHERI M, ANSARI N, et al. Reducing the impact of handovers in ground-to-train free space optical communications[J].IEEE Transactions on Vehicular Technology,2018,67(2):1292.
- [2] PLANK T, LEITGEB E, LOESCHNIGG M. Recent developments on free space optical links and wavelength analysis[C]//International Conference on Space Optical Systems and Applications. Santa Monica:IEEE,2011:14.
- [3] PAUDEL R, GHASSEMLOOY Z, MINH H L, et al. Lambertian source modelling of free space optical ground-to-train communications[C]//2012 8th International Symposium on Communication Systems, Networks & Digital Signal Processing(CSNDSP). Poznan:IEEE,2012:1.
- [4] MOHAN N, GHASSEMLOOY Z, ZVANOVEC S, et al. Relayed FSO links for ground-to-train communications[C]//2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing. Porto:IEEE,2020:1.
- [5] AKELLA J, LIU C, PARTYKA D, et al. Building blocks for mobile free-space-optical networks[C]//Second IFIP International Conference on Wireless and Optical Communications Networks. Dubai:IEEE,2005:164.
- [6] FATHI-KAZEROONI S, KAYMAK Y, ROJAS-CESSA R, et al. Optimal positioning of ground base stations in free space optical communications for high-speed trains[J].IEEE Transactions on Intelligent Transportation Systems,2018,19(6):1940.
- [7] FAN Q, ANSARI N, FENG J, et al. Reducing the number of FSO base stations with dual transceivers for next-generation ground-to-train communications[J].IEEE Transactions on Vehicular Technology,2018,67(11):11143.
- [8] 陈春俊,陈仁涛.高速列车多目标约束横向半主动控制算法研究[J].计算机测量与控制,2021,29(1):120.
- [9] 许文天,梁树林,池茂儒,等.动车组横向半主动悬挂模糊天棚控制研究[J].铁道机车车辆,2020,40(5):28.
- [10] KANG C G, HA M T, CHO Y H. Modal analysis for lateral dynamics of a high-speed train[C]//2017 11th Asian Control Conference. Gold Coast:IEEE,2017:479.
- [11] 缪慧敏.车体垂向振动对高铁自由空间光通信指向性误差和系统性能的影响分析[D].杭州:浙江科技学院,2020.
- [12] 国家铁路局.高速铁路无砟轨道不平顺谱:TB/T 3352—2014[S].北京:中国铁道出版社,2014:1.
- [13] 翟婉明.车辆-轨道耦合动力学:上册[M].4版.北京:科学出版社,2015:113,128.
- [14] 任尊松.车辆系统动力学[M].北京:中国铁道出版社有限公司,2019:158.
- [15] 罗林.轨道随机干扰函数[J].中国铁道科学,1982(1):80.
- [16] 斯克拉.数字通信:基础与应用[M].徐平平,宋铁成,叶芝慧,译.2版.北京:电子工业出版社,2010:19.
- [17] 盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.北京:高等教育出版社,2008:305.
- [18] 陈春俊.高速列车主动与半主动控制[M].成都:西南交通大学出版社,2015:35,232-233.
- [19] PROAKIS J G, SALEHI M.数字通信:中文精简版[M].张力军等,改编.5版.北京:电子工业出版社,2012:39.
- [20] WANG Q, SONG T, WU M W, et al. Influence of pointing errors on error probability of inter-satellite laser communications[C]//2016 21st OptoElectronics and Communications Conference(OECC)held jointly with 2016 International Conference on Photonics in Switching(PS). Niigata:IEEE,2016:2.
- [21] FARID A A, HRANILOVIC S. Outage capacity optimization for free space optical links with pointing errors[J].Journal of Lightwave Technology,2007,25(7):1705.
- [22] 帕普里斯,佩莱.概率、随机变量与随机过程[M].保铮,冯大政,水鹏朗,译.4版.西安:西安交通大学出版社,2012:101.
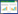 图 1 车地间FSO通信链路模型
Fig.1 Train-to-ground FSO communication link model
图 1 车地间FSO通信链路模型
Fig.1 Train-to-ground FSO communication link model