自从1895年数学家Korteweg与de Vries导出著名的浅水波(Korteweg de vries,Kdv)方程[1-2],并给出该方程的解析解,即孤子解,孤子理论便被广泛应用于非线性科学领域[3-4]。一般情况下非线性模型有多种解,孤子解是其中的一类解,孤子与非线性微分方程存在巧妙的关系,色散与非线性的共同作用产生了孤子。杨高翔[5]建立了一类具有强滞核的单种群扩散模型,并用摄动理论证明行波解的存在性,这为双线性方法求解波动方程提供了参考; 段亮等[6]基于非线性可积模型中的严格解和线性稳定分析结果,讨论了如何建立基本非线性波与调制不稳定性的精确对应关系; Yan[7]研究了Ivancevic期权定价模型在某种程度上可以替代传统的Black-Scholes期权定价模型,发现该模型在一定情况下存在畸形波现象,并选取多种参数展示了金融畸形波的动态性质; Osman等[8]构造了(2+1)维Heisenberg自旋链方程精确的孤子解,为复杂非线性偏微分方程孤子解的构造提供了思路; Rizvis等[9]用Hirota双线性方法得到(1+1)维广义超弹性杆方程的lump孤子解、多重孤子解、周期解; Hossen等[10]提出了一种求解非线性方程精确多孤子解的直接有理指数方法,给出了(1+1)维Benjamin-ono方程的双线性形式来实现截断展开,并给出波解的密度图。在常见的几类期权定价模型中,Black-Scholes模型求解涉及布朗运动、随机积分等; 蒙特卡洛方法与二叉树模型则基于计算机模拟,而求解Ivancevic期权定价模型需要严谨的数学证明与计算机仿真。综观现有文献缺乏对非线性波与多组参数的纵向比较,人们从直观上较难理解两者的对应关系。本研究将基于双线性导数方法研究Ivancevic期权定价模型孤子解,运用多组参数展示、分析孤子解的结构特征,并给出相关参数的实际意义。
1 基础知识定义1[11] 如果作用在函数f(x)、g(x)上的二元微分算子,满足以下条件:
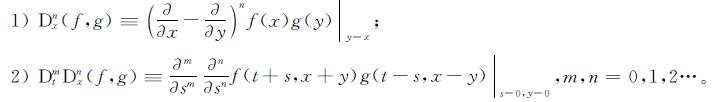
则称这种形式的算子为D-算子,也叫做Hirota导数。二元微分算子Dnx(f,g)简记为Dnxf·g,是一种用于求解非线性偏微分方程的算子,该过程通常要用到变量变换,把非线性偏微分方程转化为双线性方程,最终化为一般可求的常微分方程。
从定义上较难理解Hirota导数定义,用几个简单的例子加以说明,设f、g为关于x的函数,则
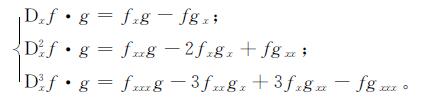
性质1 设a为常数,f为函数,ξj=pjx+wjt+η0j(j=1,2),定义1中的二元微分算子有如下结论:

非线性薛定谔(Nonlinear Schrodinger,NLS)方程被广泛应用于光学、金融系统、固体介质等非线性科学领域[12]。澳大利亚学者Ivancevic基于NLS方程、现代适应性市场假说、Elliott波市场理论[13]提出一种新的非线性期权定价模型,用以描述金融市场波动性的变化规律,称为Ivancevic期权定价模型[14],定义如下:
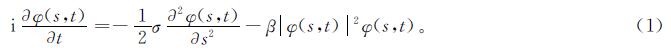
式(1)中:i=(-1)1/2; φ(s,t)为关于s、t的期权价格波函数; s为资产价格; t为时间过程; σ为离散频率系数; β为自适应市场需求量; |φ|2=φ φ*,其中φ*表示φ的共轭。
定理1 模型(1)具有单孤子解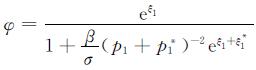 。
。
证明:假设分母为实值函数且不为0,做有理变换φ=g/f,引入Hirota导数,模型(1)变为如下形式:
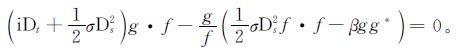
从而得到Ivancevic期权定价模型的双线性形式:
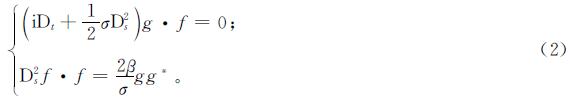
将实值函数f与复函数g展开成含小参数ε的幂级数:

再将展开式代入式(2),得
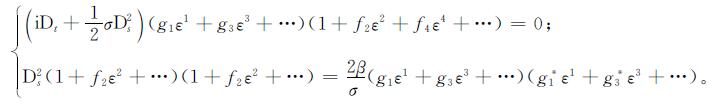
结合性质1,按ε的次幂排列,得
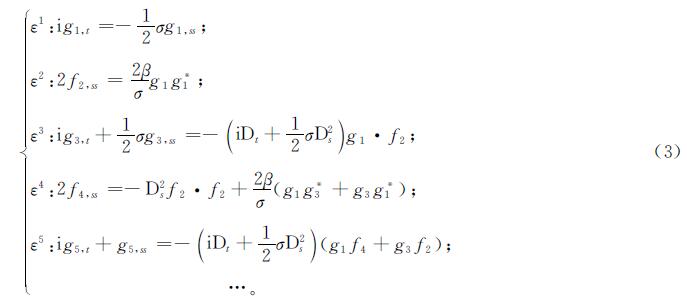
在非线性波理论里,可以选择一个指数衰减型函数刻画孤立波,从系数项ε1出发构造一组色散关系

取

将式(4)代入系数项ε2,解得:

将式(5)代入系数项ε3
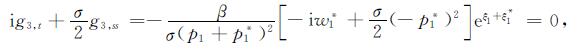
解得:
g3=0。(6)
将式(6)代入系数项ε4,解得:
f4=0。(7)
以此类推,不难得到g5=0,f6=0…,函数g、f的展开式被截断为有限项和,特别地,当ε=1时得到Ivancevic期权定价模型的单孤子解

定理1 得证。
定理2 模型(1)具有双孤子解
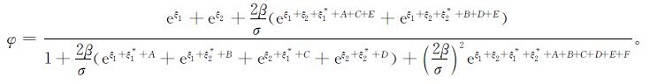
证明:由于函数g、f是线性指数函数,对函数g1应用性质1,取
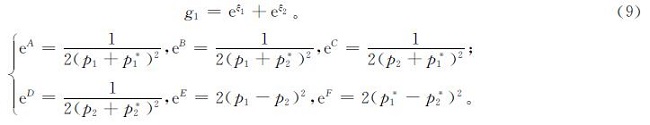
将式(9)代入系数项ε2,求解f2:
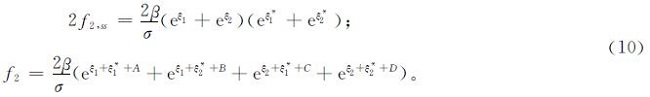
将式(10)代入系数项ε3,求解g3:
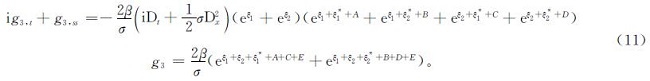
再代入系数项ε4,解得:

以此类推,不难发现
g5=0。(13)
依次将结果代入系数项ε5,ε6,…,发现f6=0,g7=0,…,函数g、f的展开式被截断为有限项和,特别地,当ε=1时得到Ivancevic模型的双孤子解

定理2 得证。
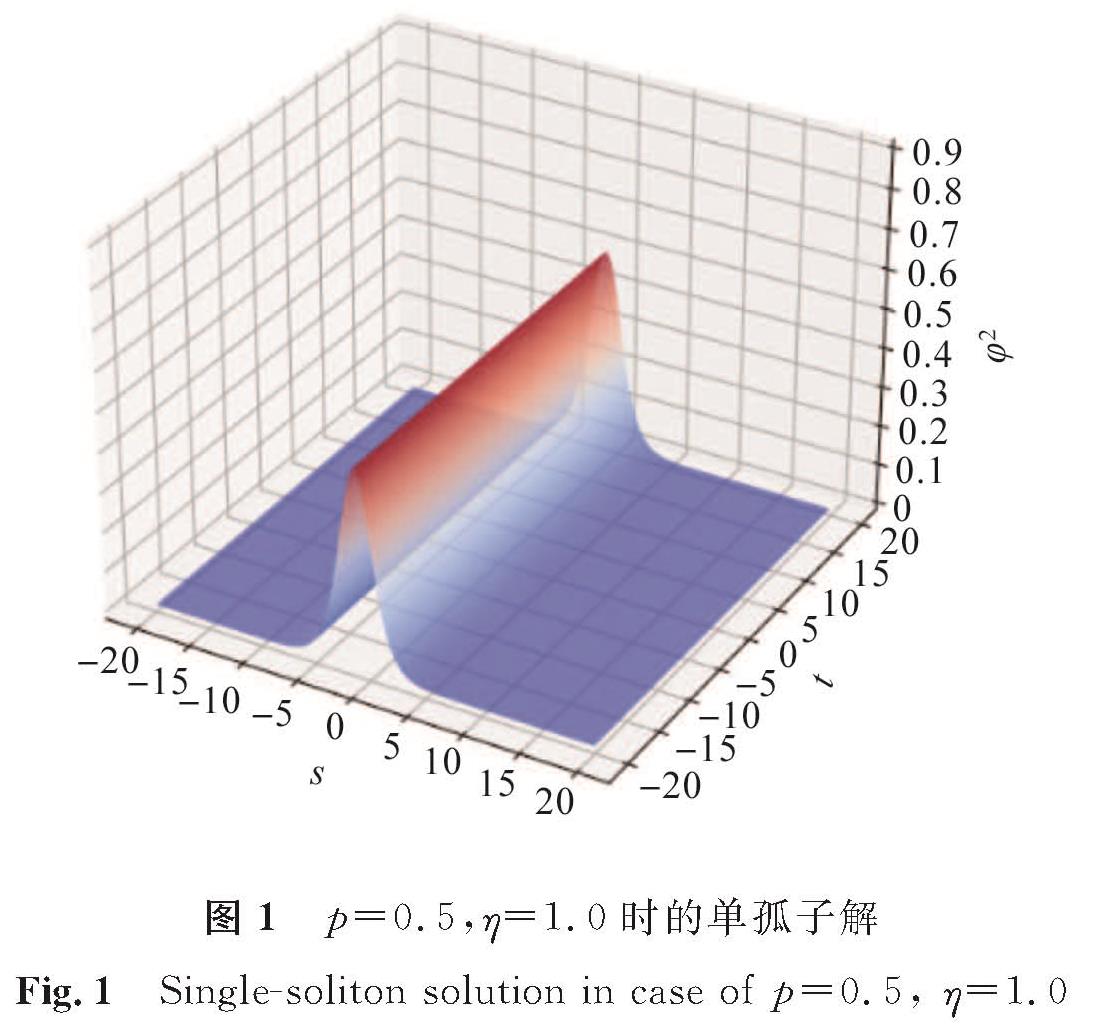
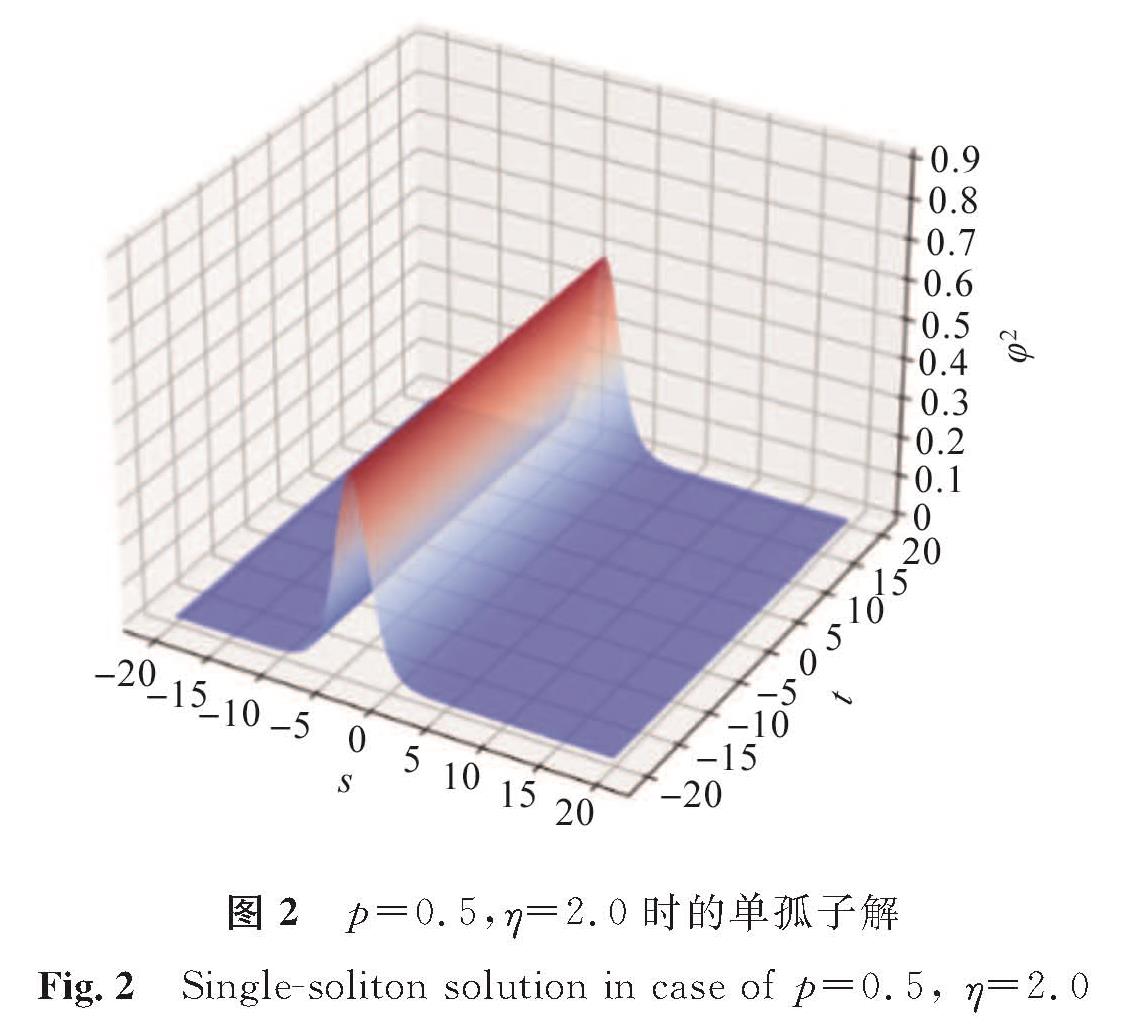
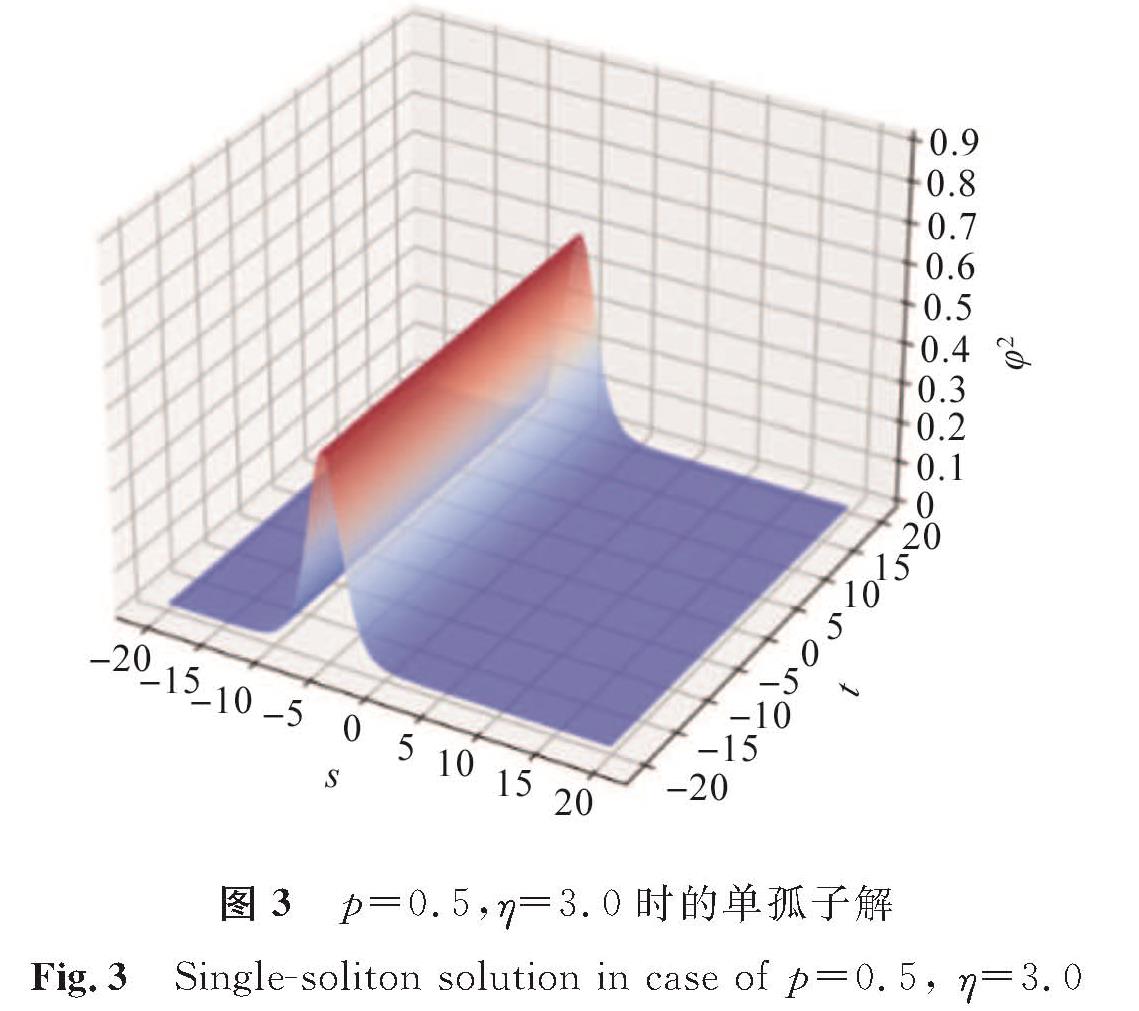
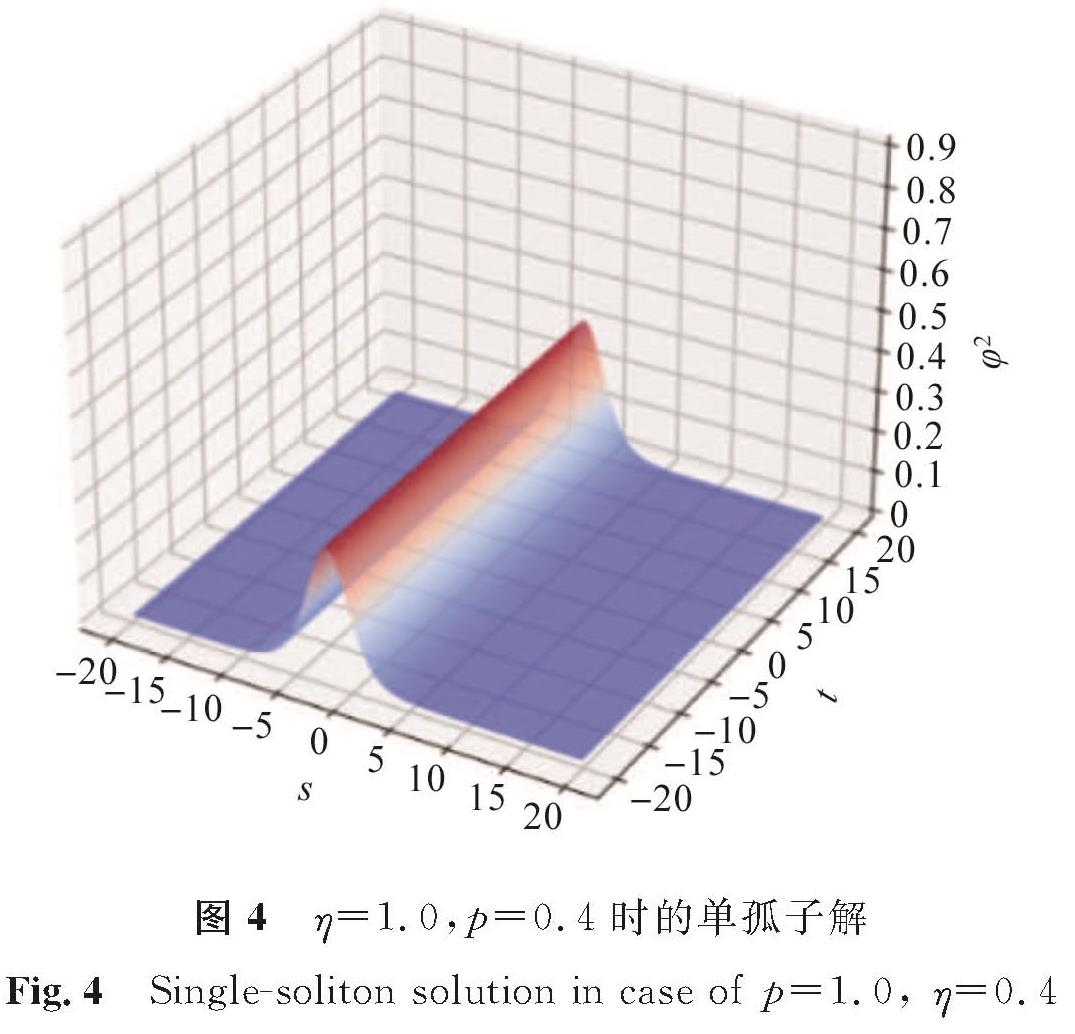
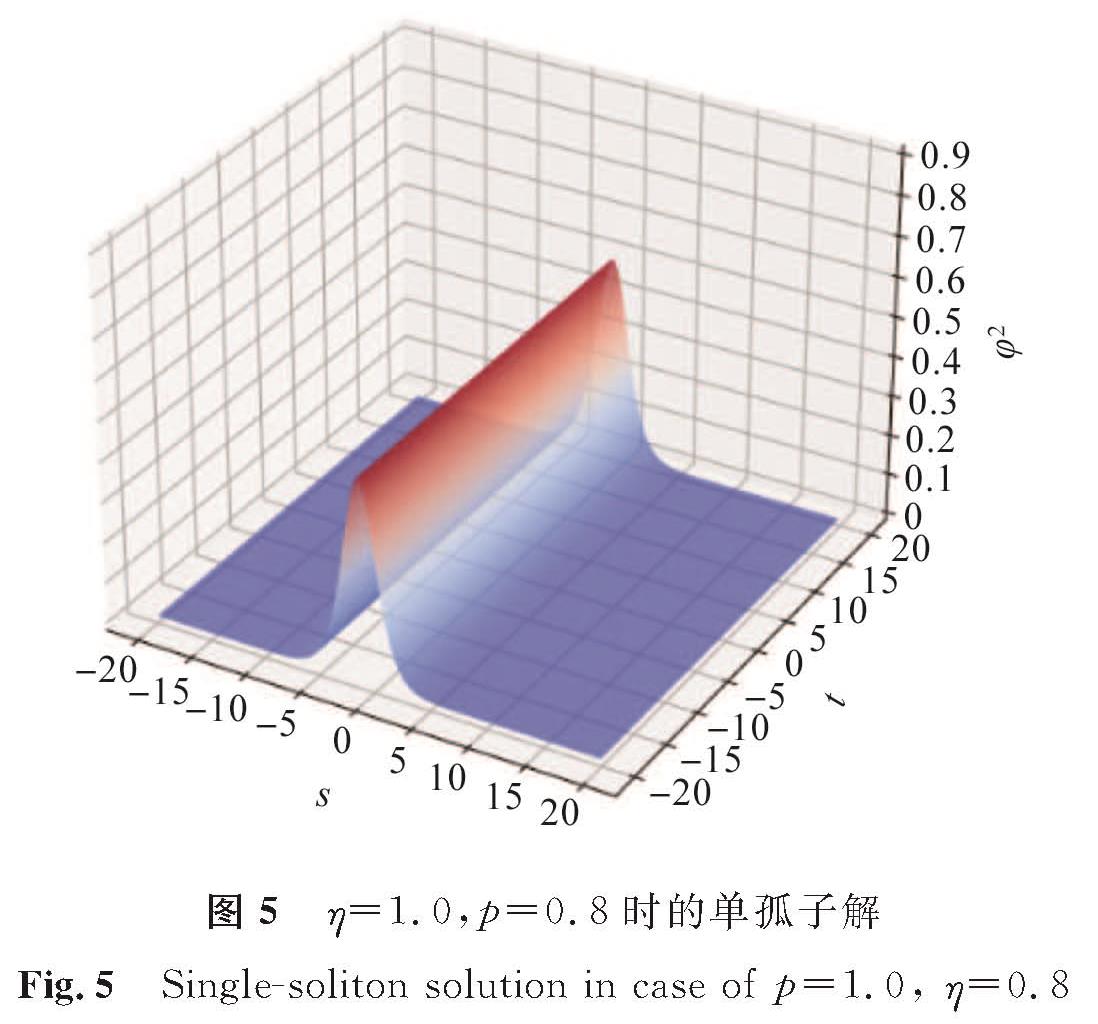
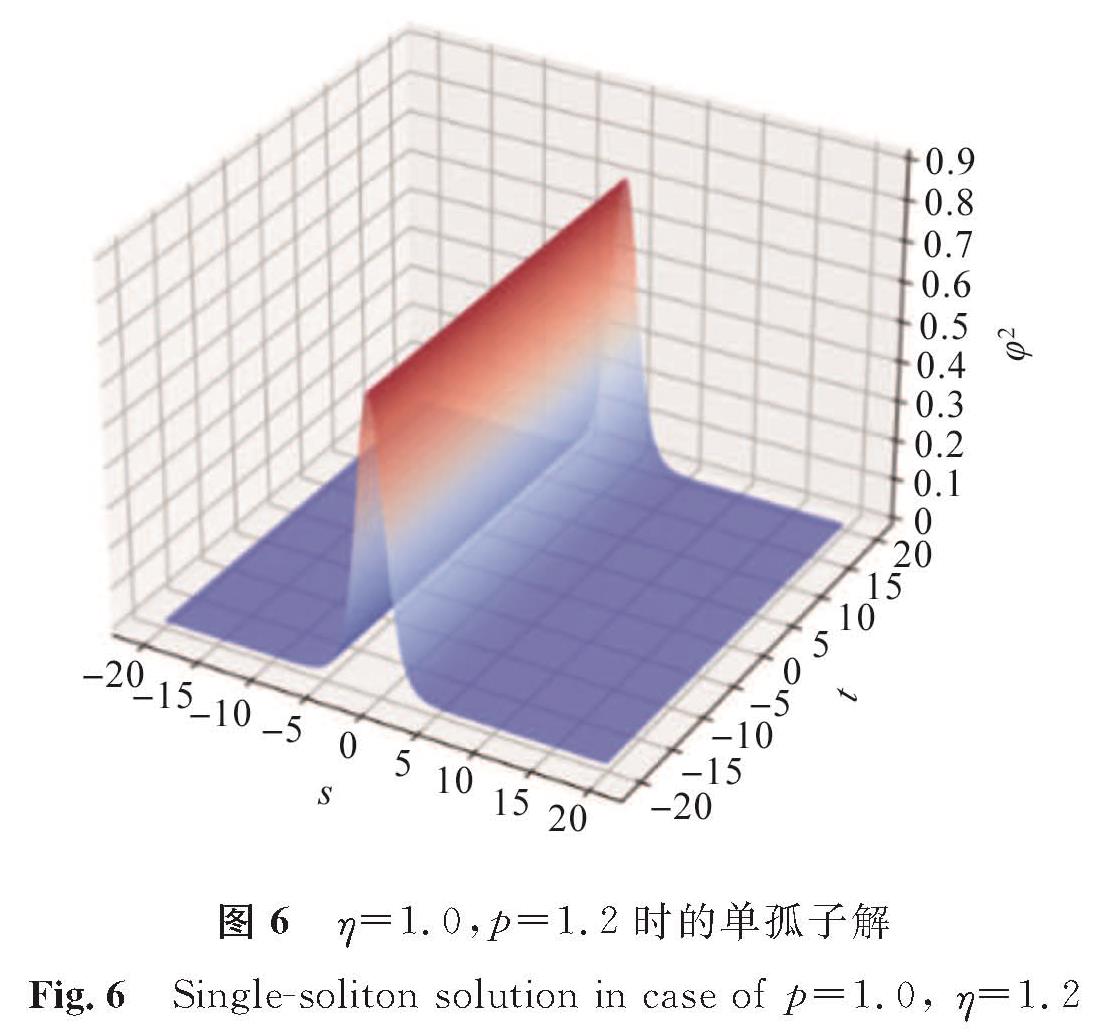
3 数值试验通过控制变量法分别控制参数p、η的取值,探究这两个参数对Ivancevic期权定价模型的影响效果。在两类孤子解式(8)和式(14)中:φ2为关于s与t的波动密度函数; 取辅助参数ε=1.0,离散频率系数σ=2.0,自适应市场需求量β=1.0。当p=0.5,η取1.0、2.0、3.0时,模型(1)单孤子解如图1~3所示; 当η=1.0,p取0.4、0.8、1.2时,模型(1)单孤子解如图4~6所示。
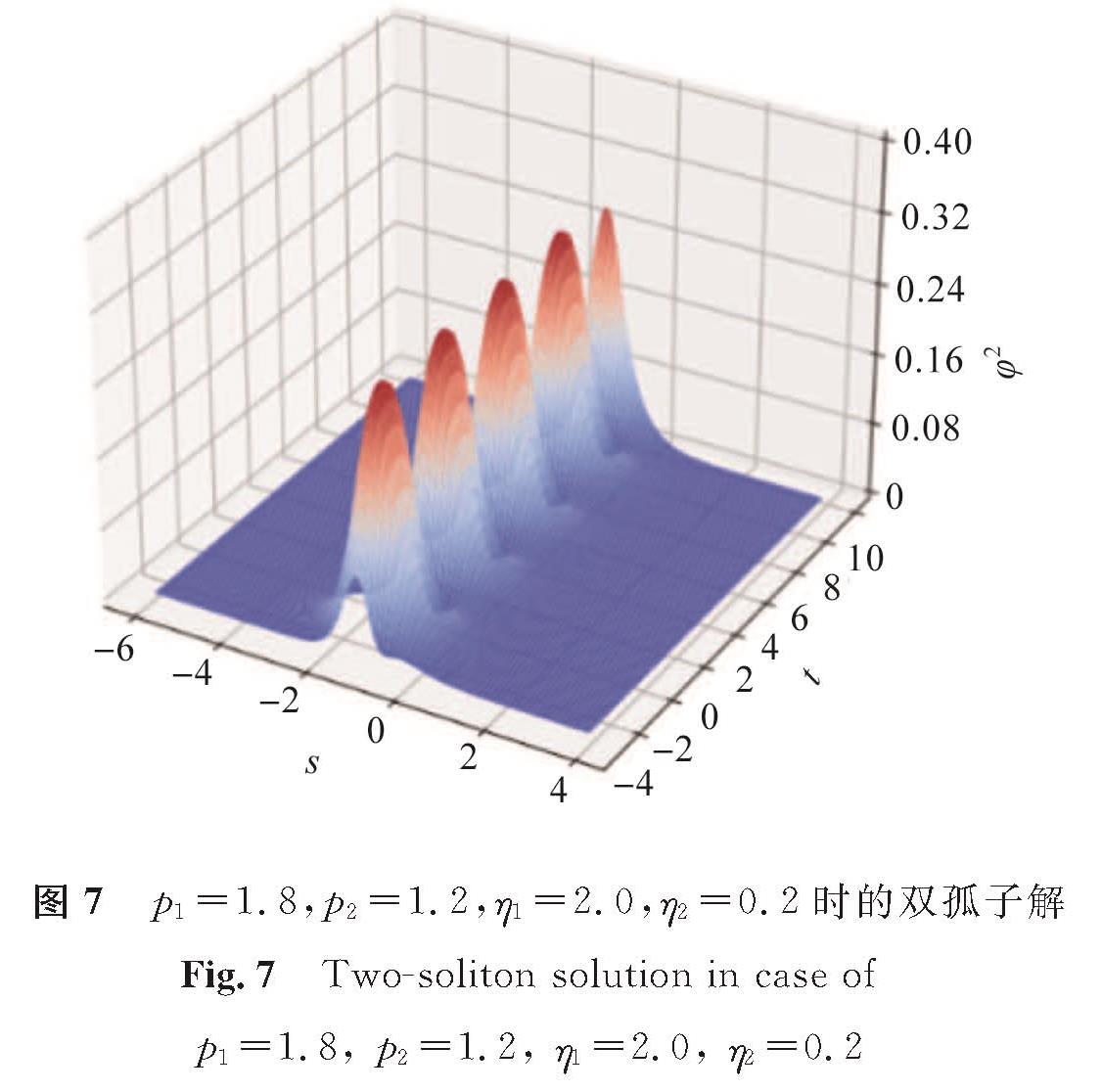
图7 p1=1.8,p2=1.2,η1=2.0,η2=0.2时的双孤子解
Fig.7 Two-soliton solution in case of p1=1.8, p2=1.2, η1=2.0, η2=0.2
比较图1~3可以看出,当p不变时,密度函数φ2不变,但孤子位置随η增大向左缓慢平移,这说明η表示孤子的相位,控制孤子的位置; 比较图4~6可以看出,当η不变时,孤子的相位不发生变化,但波峰高度随p的增大逐渐变得陡峭,说明p表示孤子的振幅,控制密度函数φ2的波峰。比较两组试验能够得出模型(1)精确解中参数的意义。模型(1)的双孤子解的结构更为复杂,当取p1=1.8,p2=1.2,η1=2.0,η2=0.2一组参数时,双孤子解如图7所示,观察不同时刻孤子的演化过程发现,双孤子因受到多种参数的影响而发生了碰撞。
4 结 语基于Hirota双线性方法给出了Ivancevic期权定价模型的两类孤子解,本研究证明了该模型确实存在孤子解并选取参数展示这种非线性方程的动态性质。分析了参数p与η的物理意义,发现模型解的结构受多种参数影响,当一个或多个参数发生变化时,波动特征也相应改变。可以将这种非线性波动特征应用于其他领域,如金融数学等,为研究股票、证券等提供思路。在今后的研究中也可以探究拉普拉斯变换、变分等方法求解类似波动方程。
- [1] EFIM P, TATIANA T, TARMO S. The structure of algebraic solitons and compactons in the generalized Korteweg-de Vries equation[J].Physica D:Nonlinear Phenomena,2021,419(9):132785.
- [2] STEPHEN A, HAMIDREZA N, ELENA R. Travelling wave solutions on a non-zero background for the generalized Korteweg-de Vries equation[J].Journal of Physics A:Mathematical and Theoretical,2021,54(8):5701.
- [3] 周昱,张远,王颖,等.具有2n+1次非线性的薛定谔方程暗孤子特性[J].光学学报,2020,40(9):165.
- [4] 柴汉鹏.几类非线性发展方程的孤立波与畸形波的研究[D].北京:北京邮电大学,2019.
- [5] 杨高翔.一类具有强时滞核的单种群扩散模型的行波解[J].华东师范大学学报(自然科学版),2020(4):18.
- [6] 段亮,刘冲,赵立臣,等.基本非线性波与调制不稳定性的精确对应[J].物理学报,2020,69(1):103.
- [7] YAN Z. Financial rogue waves[J].Communications in Theoretical Physics,2010,54(11):947.
- [8] OSMAN M, TARIQ K, BEKIR A, et al. Investigation of soliton solutions with different wave structures to the(2+1)-dimensional heisenberg ferromagnetic spin chain equation[J].Communications in Theoretical Physics,2020,72(3):9.
- [9] RIZVI S, SEADAWY A, YOUNIS M, et al. Lump-soliton, lump-multisoliton and lump-periodic solutions of a generalized hyperelastic rod equation[J].Modern Physics Letters B,2021,35(11):2150188.
- [10] HOSSEN M B, HARUN O R, ALI M Z. Study on exact solutions of Benjamin-ono equation via bilinear approach[J].Partial Differential Equations in Applied Mathematics,2021(3):100035.
- [11] GU C. Soliton theory and its applications[M].Berlin Heidelberg:Springer-Verlag,1995:403.
- [12] YAN Z. Vector financial rogue waves[J].Physics Letters A,2011,375(48):4274.
- [13] 马金龙,马非特.金融市场高频数据挖掘的新进展:金融孤子(非欧几何)构造投资模式的实盘交易[J].华南金融电脑,2006(6):8.
- [14] 宋丽军,徐晓雅,王艳.Four-soliton solution and soliton interactions of the generalized coupled nonlinear schrodinger equation[J].Chinese Physics B,2020,29(6):261.
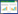 图 1 p=0.5,η=1.0时的单孤子解
Fig.1 Single-soliton solution in case of p=0.5, η=1.0
图 1 p=0.5,η=1.0时的单孤子解
Fig.1 Single-soliton solution in case of p=0.5, η=1.0