浙江科技学院学报

费正顺,王焰平,龚海波,等.一种改进的近端策略优化算法[J].浙江科技学院学报,2023,35(01):23-29.[doi:10.3969/j.issn.1671-8798.2023.01.004]
FEI Zhengshun,WANG Yanping,GONG Haibo,et al.On an improved algorithm of proximal policy optimization[J].Journal of Zhejiang University of Science and Technology,2023,35(01):23-29.[doi:10.3969/j.issn.1671-8798.2023.01.004]

点击复制

一种改进的近端策略优化算法

[PDF全文]

费正顺,王焰平,龚海波,项新建,郭峻豪

(浙江科技学院自动化与电气工程学院,杭州 310023)

收稿日期:2021-08-30
基金项目:浙江省重点研发计划项目(2018C01085); 浙江省自然科学基金项目(LQ15F030006); 浙江省教育厅科研项目(Y202249418); 浙江科技学院研究生科研创新基金项目(2021yjskc04)
通信作者:项新建(1964— ),男,浙江省永康人,教授,硕士,主要从事人工智能、机器人技术研究。E-mail:188002@zust.edu.cn。

近端策略优化(proximal policy optimization,PPO)是从一个已知的分布附近来采样估计另一个分布,通过用新策略在老策略的附近学习来实现优化的,其中老策略作为新策略的近似分布。【目的】针对PPO算法在强化学习中学习效率及收敛性不够好的问题,提出一种改进的PPO算法。【方法】首先提出一种新损失函数来更新PPO算法中的网络参数,采用泛化优势估计(generalized dominance estimation,GAE)对优势函数进行描述; 然后采用类似异步优势演员-评论家(asynchronous actor-critic,A3C)算法中的多线程策略来训练智能体; 最后设计新的参数更新方式来实现对主副两种网络中的参数更新。【结果】本方法能够使智能体更快地完成学习训练,其训练过程中收敛性更好; 由于多线程,其算法的训练速度会比常规的PPO算法至少快5倍。【结论】改进的PPO算法其性能更好,这为后续强化学习算法的研究提供了新思路。

关键词：强化学习; 近端策略优化; 泛化优势估计; 多线程

On an improved algorithm of proximal policy optimization

FEI Zhengshun, WANG Yanping, GONG Haibo, XIANG Xinjian, GUO Junhao

(School of Automation and Electrical Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, Zhejiang, China)

Proximal policy optimization(PPO)is to sample and estimate another distribution from the vicinity of a known distribution, and realize optimization by learning from the vicinity of the old policy with the new one, in which the old policy is the approximate distribution of the new one. [Objective] Aiming at the problem of the undesirable efficiency and convergence of PPO algorithm in reinforcement learning, an improved PPO algorithm was proposed. [Method] Firstly, a new loss function was proposed to update the network parameters in PPO algorithm, and generalized dominance estimation(GAE)was adopted to describe the dominance function; secondly, a multithreading strategy similar to that in the asynchronous advantage actor-critic(A3C)algorithm was used to train agent; finally, a new parameter update method was designed to realize the update of parameters in both primary and secondary networks. [Result] The simulation results show that this method can facilitate the agent's faster learning and training, with better convergence in its training process; thanks to multithreading, its training speed will be at least 5 times faster than the conventional PPO algorithm. [Conclusion] The performance of the improved algorithm of proximal policy optimization is better, which can provide a new idea for the subsequent study of reinforcement learning algorithm.

Keywords：reinforcement learning; proximal policy optimization; generalized dominance estimation; multithreading

引言

强化学习属于机器学习的一种类型,根据动物心理学的相关原理模仿人类和动物学习的试错机制,它是一种通过与环境相互作用来学习从状态到行为的映射关系,从而使累积预期收益最大化的方法。目前它已经在很多领域得到运用,如工业制造^[1]、机器人系统^[2-3]、机器人控制^[4]、自动驾驶^[5]等。

近些年来,随着强化学习研究的不断深入,许多相关算法也涌现出来。其中比较有代表性的是深度学习网络算法(deep Q-network,DQN^[6]),它将神经网络运用于强化学习,能够有效地避免因过多的行为状态对信息造成的计算机内存不足。DQN算法主要是通过价值(或奖惩值)来选择行为。有研究者提出策略梯度(policy gradients,PG^[7])算法,即直接通过状态来输出动作或动作的概率,由于其遵循的是梯度法,会向着优化策略的方向进行更新,因此具有很好的收敛性,但缺点是在使用梯度法对目标函数进行求解时,容易收敛到局部最小值。在演员-评论家(actor-critic^[8],AC)算法中,actor是基于概率来选择行为,critic用于评判actor的行为得分,然后actor又会根据critic的评分修改行为的概率^[9]。这样就可以解决策略梯度算法在回合更新时效率低的问题,但存在难收敛的问题。为此深度确定性梯度(deep deterministic policy gradient,DDPG^[10])算法被提出,但它只在连续动作区间上输出一个动作值。为了解决AC算法难以收敛及加快其训练速度,异步优势演员-评论家(asynchronous advantage actor-critic,A3C^[11])算法将AC算法放到多线程中进行同步训练。而置信域策略优化(trust region policy optimization,TRPO^[12])算法的出现解决了A3C算法在平衡模型的方差和偏差时存在波动的问题,能够确保策略模型在优化时单调提升。随后在TRPO的算法框架基础上,深度思考(DeepMind)公司提出了近端策略优化(proximal policy optimization,PPO^[13])算法。

PPO算法的提出解决了之前强化学习算法表现出的不足,比如传统的策略梯度方法数据利用效率低和鲁棒性差,信任区域策略优化(TRPO)算法相对复杂。其主要优势体现在:易于部署且迭代过程中其方差较小,使用方便,训练起来也比较稳健。PPO算法是一种用来解决策略梯度不好确定学习率(或者训练步长)问题的策略。在优化学习过程中如果训练步长过大,学出来的策略会难以收敛,但如果训练步长太小,则完成训练耗费的时间又会过长。PPO算法利用新旧策略的比例来限制新策略的更新范围,使得策略梯度对过大的训练步长不太敏感。对此DeepMind公司在人工智能研究(OpenAI)公司发表的PPO算法基础上提出了新的PPO算法^[14],其中单线程的PPO算法与OpenAI公司的PPO算法在更新actor网络参数θ,及critic网络参数Φ的方式上不同。在此基础上,OpenAI公司又提出分布式PPO算法(distributed proximal policy optimization,DPPO^[14]),采用多线程来加快智能体的训练效率。

一般的PPO算法在学习效率和收敛性上表现得不够理想,为此本研究提出一种改进的PPO算法:首先将泛化优势估计(generalized dominance estimation,GAE)作为优势函数来估计优势; 然后参考文献[13]在actor网络结构中选取网络参数θ的损失函数,参考文献[14]在参数θ的更新过程中选取对相对熵(Kullback-Leibler,KL)散度项的限制,以此来更新参数θ,再参考文献[14]在critic网络结构中选取网络参数Φ的损失函数; 最后提出一种新的主副网络参数更新方式。为验证算法的效果,我们在OpenAI gym模块的经典控制环境及复杂的mujoco环境中进行了仿真试验。

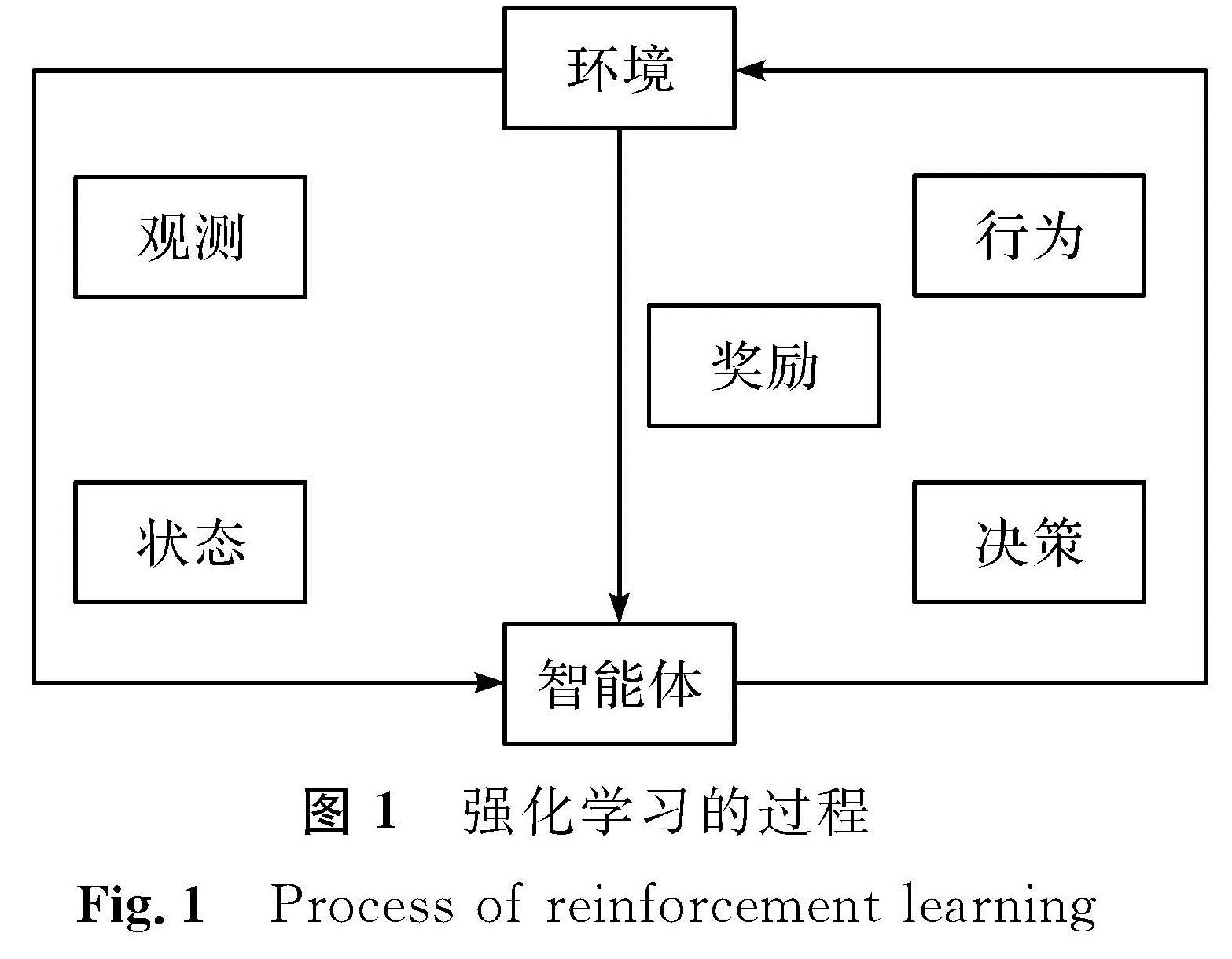
1 强化学习介绍1.1 强化学习模型

强化学习是一个马尔科夫决策过程,此过程可用一个五元组^[15]构成:{S,A,P,R,γ}。其中:S为环境的状态集,状态是智能体对环境的感知; A为智能体的动作集,是智能体在当前的强化学习任务中选择的动作范围; P为状态转移概率,指智能体采取某一个动作后从当前状态到下一个状态的概率; R为奖励机制,指智能体在当前状态下采取某一个动作后,环境反馈给智能体的奖励; γ为衰减系数(或折扣因子),用于计算当前状态的累计回报。强化学习是智能体与环境相互作用的过程。首先,智能体观测自己的当前状态,然后根据观测结果做出决策并采取相应的行为。一方面,该行为与环境相互作用,环境会对智能体的行为进行奖励; 另一方面,该行为使得智能体从当前状态进入下一个状态。如此循环往复,直至结束循环,强化学习的过程^[16]如图1所示。

图1 强化学习的过程<br/>Fig.1 Process of reinforcement learning

图1 强化学习的过程
Fig.1 Process of reinforcement learning

1.2 值函数

在强化学习过程中,状态到行为的映射关系可称之为策略^[17],指在各个状态下智能体所采取的行为或行为概率。值函数是强化学习算法中最基础的评价指标,这个指标反映算法的优劣,它是智能体在给定的状态和最优策略下采取某个动作或行为时的优劣程度。值函数^[18]主要分两种:一种为状态值函数V_π(s),是从状态s开始,按照某种策略行为产生的长期回报期望; 另一种为状态动作值函数Q_π(s,a),是在状态s和策略π下,采取动作a,按照某种策略行为产生的长期回报期望。

2 改进的PPO算法构造2.1 优势函数的选取

优势函数指智能体在状态s下,采取动作a时,其相应动作下产生的平均优势,从数量关系来看,就是随机变量相对均值的偏差,是将状态行为值函数归一化到值函数的基线上。这样有助于提高智能体学习的效率,减小方差及避免方差过大带来的过拟合。本研究采取了GAE作为优势函数的估计方式,其作用是能够平衡偏差和误差给价值函数及回报带来的影响。优势函数的表达式如下:

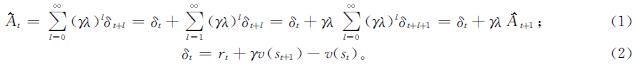
式(1)～(2)中:δ_t为时序差分误差,是每一时刻的现实值与估计值之间的差距; λ为超参数,用于调节方差与偏差之间的平衡,当λ=0时,就是计算时序差分误差; 当λ=0时,就变成了蒙特卡罗^[19]目标值和价值估计之间的差。

2.2 目标函数的选取

本研究选取变量β来控制约束项和目标项之间的权重关系,将KL散度作为目标函数的惩罚项,其目标函数也称为actor网络的损失函数,表达式如下:

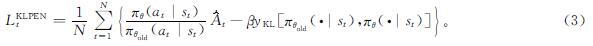
式(3)中:(π_θ(a_t|s_t))/(π_{θ_old}(a_t|s_t))为新老策略概率的比例; θ_old为策略未更新前的参数; y_KL(π_{θ_old}(·|s_t),π_θ(·|s_t))为KL散度项,表示新老策略之间的差距,主要是限制新老策略的更新幅度。

在式(3)中,令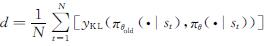,为了计算训练数据平均KL散度的阈值,设定一个目标值d_target。本研究对KL散度项加了一个限制条件,在每次更新actor网络参数θ的过程中,限制d>4d_target,而对它的约束可以通过d和d_target的关系调整β来实现:1)如果d<d_target/1.5,β←β/2,相当于放松KL约束限制; 2)如果d>d_target×1.5,β←β×2,相当于增强KL约束限制。更新后的β值将会在下一轮优化中发挥作用。

用来更新critic网络参数Φ的损失函数

2.3 主副两种网络结构的参数更新方式

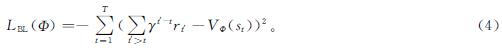
本研究根据A3C算法及在DPPO算法中用多线程训练智能体^[14]的方式,将单线程的PPO算法改成了多线程的PPO算法。DPPO算法与PPO算法的网络结构都是基于actor及critic结构,与A3C算法均有两套网络结构,即主副网络。其中副网络相当于主网络的参数,但主副网络的参数更新方式不同。在此基础上,本研究提出了一种新的主副网络参数更新方式。

由A3C算法原理可知,其工作原理就是将AC算法放到多线程中进行同步训练,其主副网络的参数更新方式是:1)各个线程均采用一个CPU(核)参与训练; 2)各个线程将主网络的参数复制过来与环境交互; 3)交互之后各个线程均会计算出各自的梯度,并将其推送给主网络,用来更新主网络的参数; 4)参数更新后,主网络再将其推送回副网络(各个线程)。如此循环。

而对于DPPO算法,其主副网络参数更新方式是:1)将各个线程推送到不同的环境中(环境的个数取决于电脑CPU核的个数),主网络会控制各个线程在各自的环境中去收集数据(数据是由智能体训练时产生的); 2)分别对actor与critic中的网络参数θ和Φ求梯度; 3)把这些梯度传送到主网络中,主网络会对所有线程推送过来的梯度求平均后,更新主网络的参数; 4)将更新后的参数推送回各个线程。如此循环。

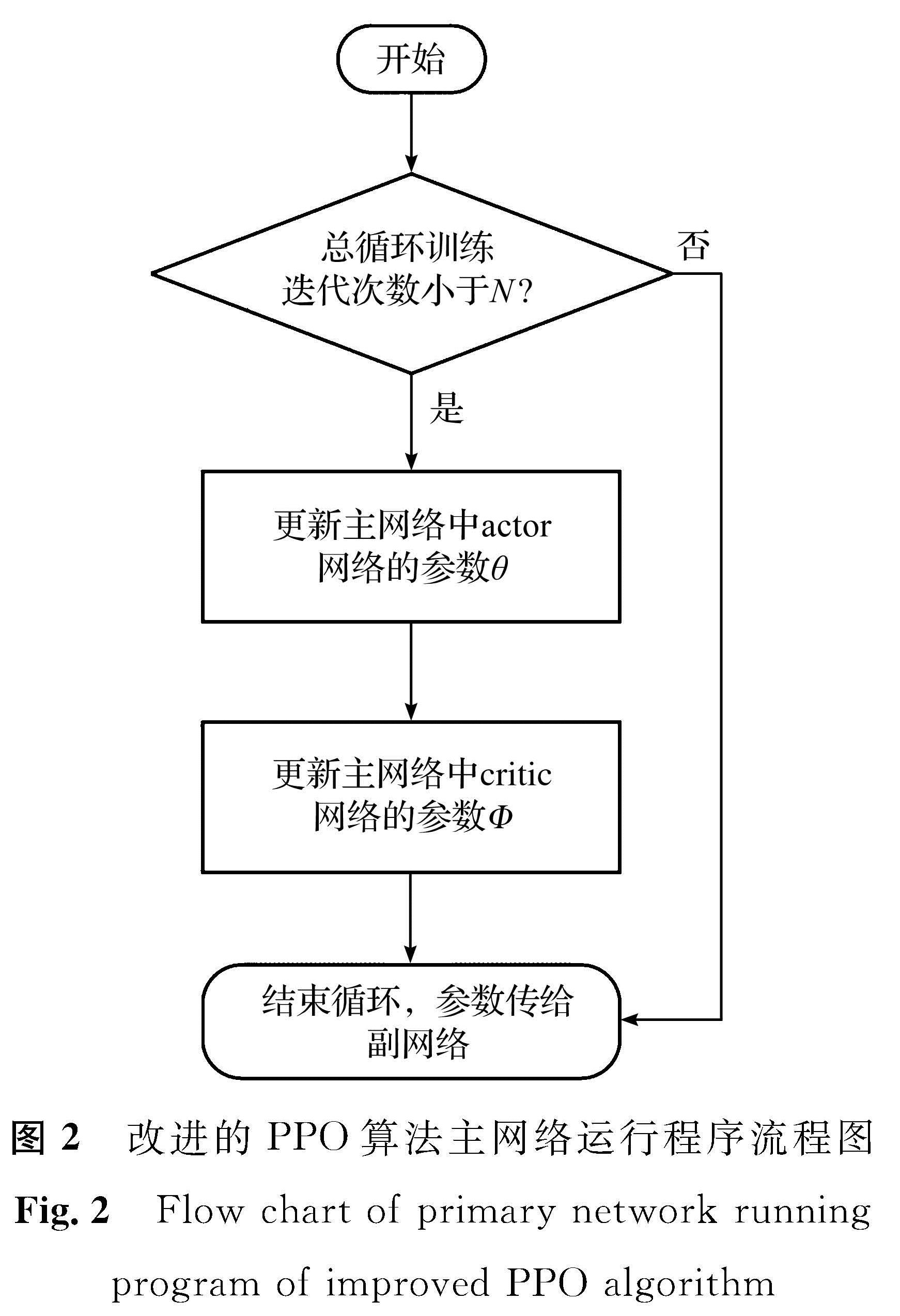
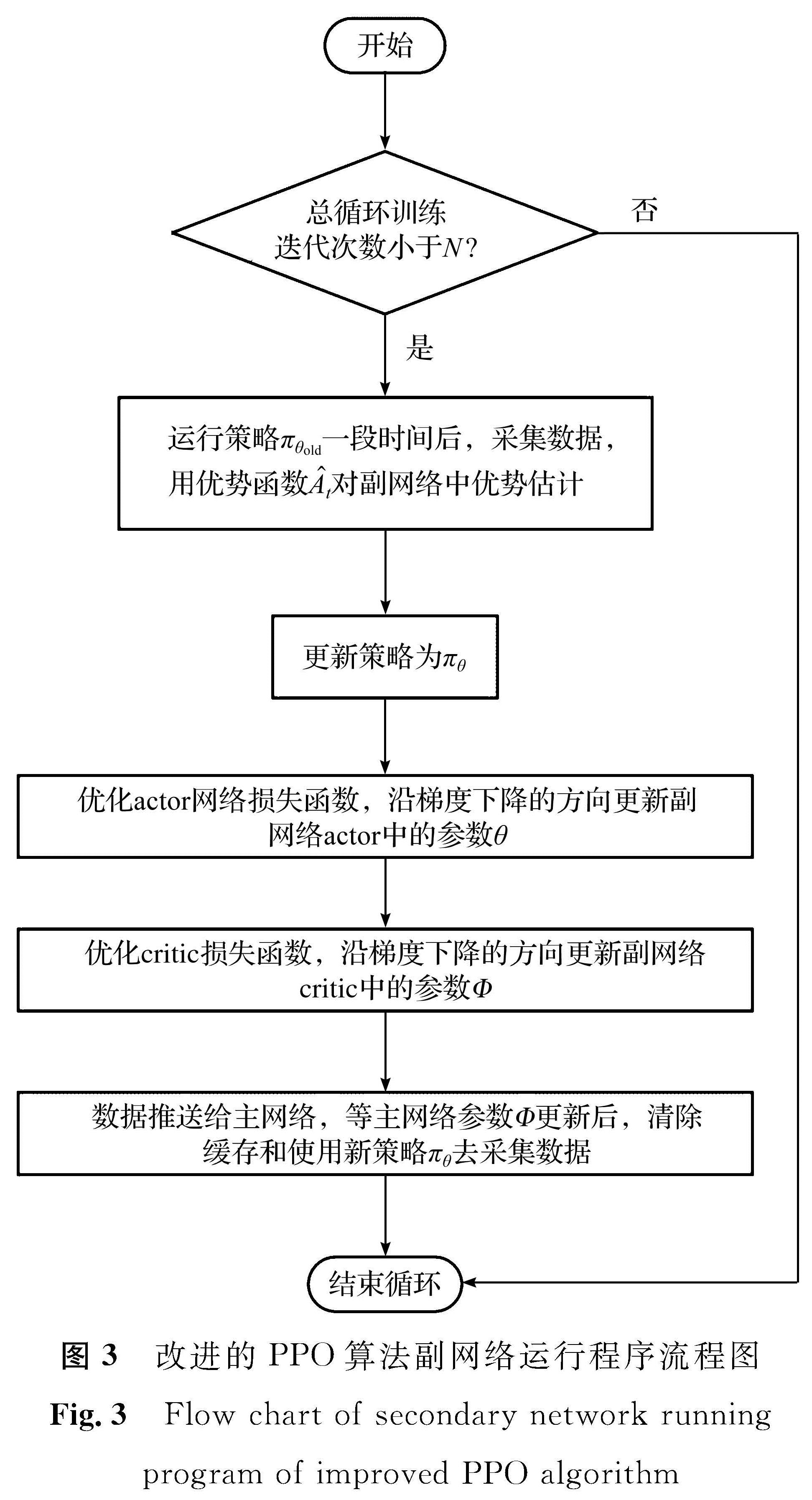
而本研究的主副网络更新方式则是:1)将各个线程推送到不同的环境中去,让主网络来控制各个线程,在各自的环境中去收集数据; 2)用Adam优化器优化各自的学习率和最小化损失函数(沿梯度下降的方向更新网络中的参数)后,将各自的经验(actor与critic中的网络参数θ(s,a,A_t)和Φ(s,r))全部推送到主网络中; 3)将不同的经验放到一起去进行更新; 4)各个线程会清空之前缓存的数据; 5)主网络再将更新好的参数推送给各个线程; 6)各个线程会更新策略,让智能体继续进行训练,从而重新开始收集数据。如此循环。其中改进的PPO算法主网络、副网络运行程序流程图分别如图2及图3所示。图2中:N为智能体训练时总的迭代次数。

图2 改进的PPO算法主网络运行程序流程图<br/>Fig.2 Flow chart of primary network running program of improved PPO algorithm

图2 改进的PPO算法主网络运行程序流程图
Fig.2 Flow chart of primary network running program of improved PPO algorithm

图3 改进的PPO算法副网络运行程序流程图<br/>Fig.3 Flow chart of secondary network running program of improved PPO algorithm

图3 改进的PPO算法副网络运行程序流程图
Fig.3 Flow chart of secondary network running program of improved PPO algorithm

3 试验及仿真3.1 环境的搭建

OpenAI gym环境是在强化学习中应用最广泛的试验环境,其中内置了上百种试验环境,如经典控制环境、算法环境、mujoco环境、文字游戏环境、Atari视频游戏环境等。本研究分别在gym模块经典控制环境及复杂的mujoco环境中进行了仿真测试。其中,经典控制环境“Pendulum-v0”如图4所示,钟摆从一个随机位置开始,通过训练使其摆动起来从而保持直立; mujoco环境“Ant-v3”如图5所示,为一个简单的三维四足机器人,通过训练使其学会行走; “Hopper-v3”如图6所示,为一个单腿的智能体,通过训练使其向前跳跃。在这3种环境场景下对本研究提出的改进的PPO算法进行了测试,同时与一般的PPO算法进行对比。

图4 “Pendulum-v0”<br/>Fig.4 “Pendulum-v0”

图4 “Pendulum-v0”
Fig.4 “Pendulum-v0”

图5 “Ant-v3”
Fig.5 “Ant-v3”

图6 “Hopper-v3”
Fig.6 “Hopper-v3”

本研究利用Python下深度学习框架tensorflow进行编程,利用多线程来把单线程变成了多线程和队列来存放单线程收集的数据。运行硬件环境为处理器Intel(R)Core(TM)i5-1035G1 CPU(8核),显卡AMD Radeon(TM)630及Intel(R)UHD Graphics。

3.2 算法训练及结果分析

将改进的PPO算法及PPO算法在gym试验环境中进行测试。其中经典控制环境中“Pendulum-v0”仿真试验为试验一; 复杂的mujoco环境中“Ant-v3”“Hopper-v3”分别为试验二和试验三。其中训练过程中相同参数设置如下:actor的学习率为0.000 1,critic的学习率为0.000 2,λ为0.98,γ为0.9,β为0.5,y_{KL_target}值为0.01。

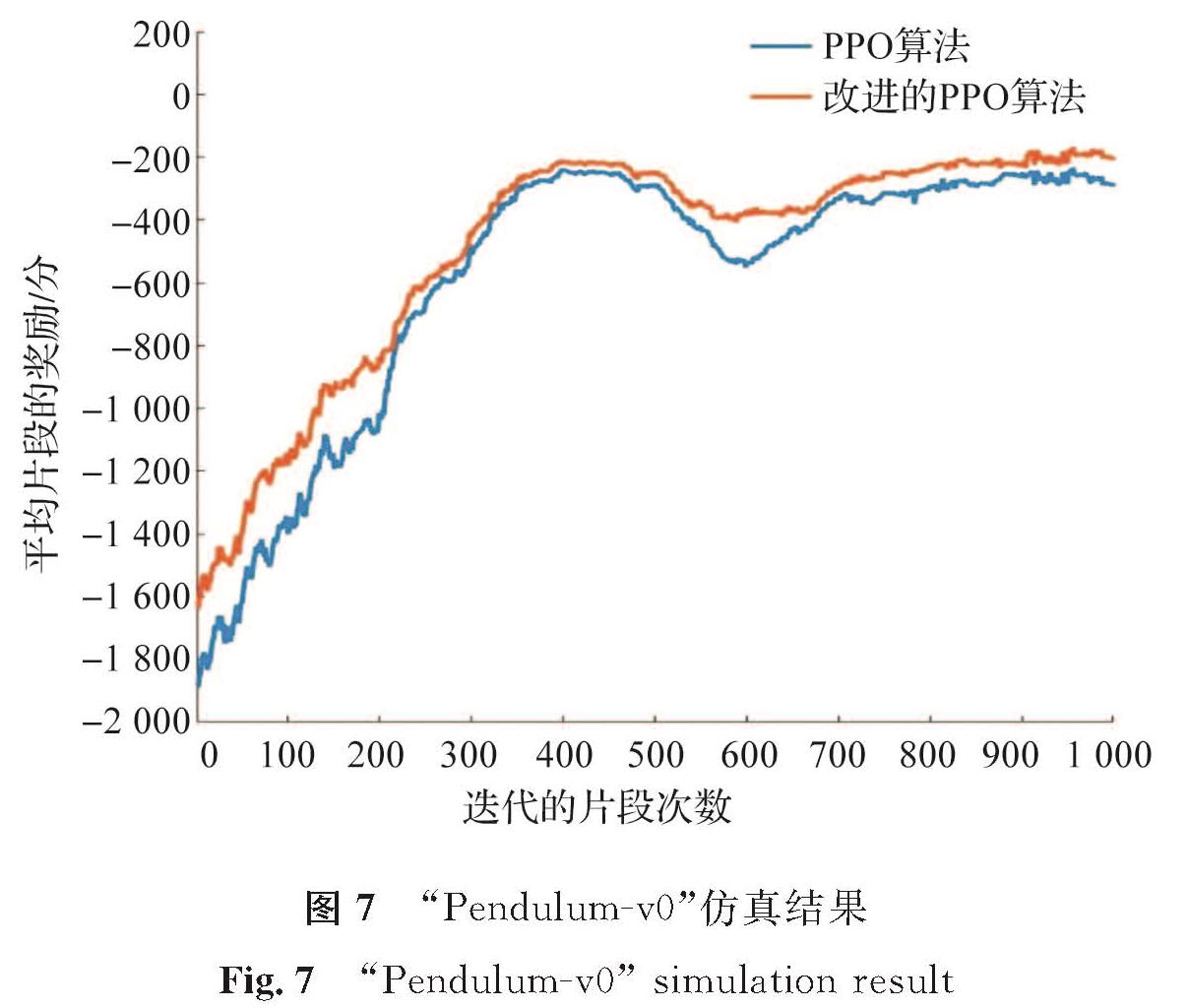
试验一:环境为“Pendulum-v0”,其他参数的设置情况如下:最大迭代的片段次数为1 000,每个片段最大训练次数为200,动作限制在[-2,2]之间,模型经过1 000次迭代训练,其迭代的片段次数及平均片段的奖励如图7所示。

图7 “Pendulum-v0”仿真结果<br/>Fig.7 “Pendulum-v0” simulation result

图7 “Pendulum-v0”仿真结果
Fig.7 “Pendulum-v0” simulation result

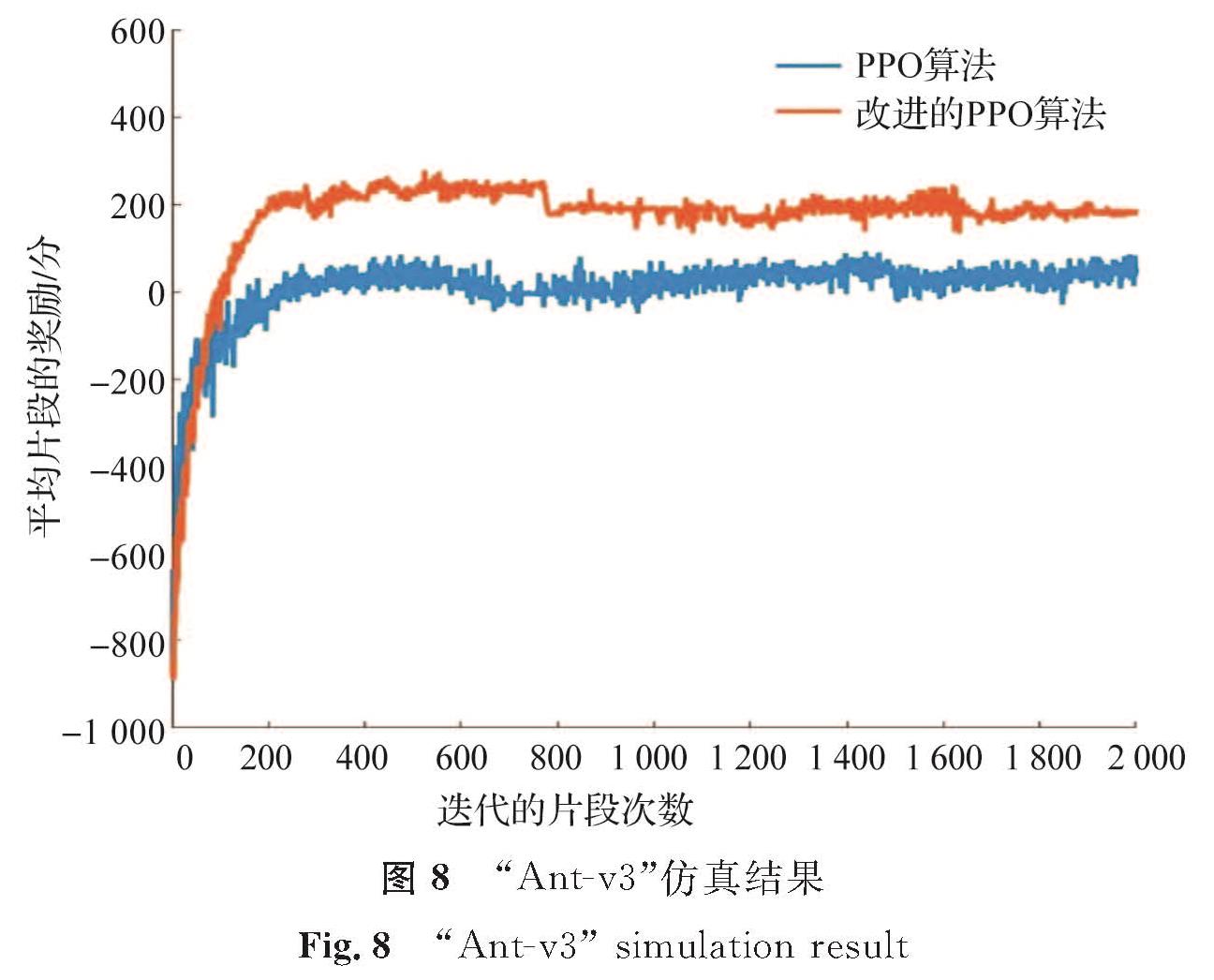
试验二:环境为mujoco模拟器中的“Ant-v3”,其他参数的设置情况如下:最大迭代的片段次数为2 000,每个片段最大训练次数为300,动作限制在[-8,8]之间,模型经过2 000次迭代训练,其迭代的片段次数及平均片段的奖励如图8所示。

图8 “Ant-v3”仿真结果<br/>Fig.8 “Ant-v3” simulation result

图8 “Ant-v3”仿真结果
Fig.8 “Ant-v3” simulation result

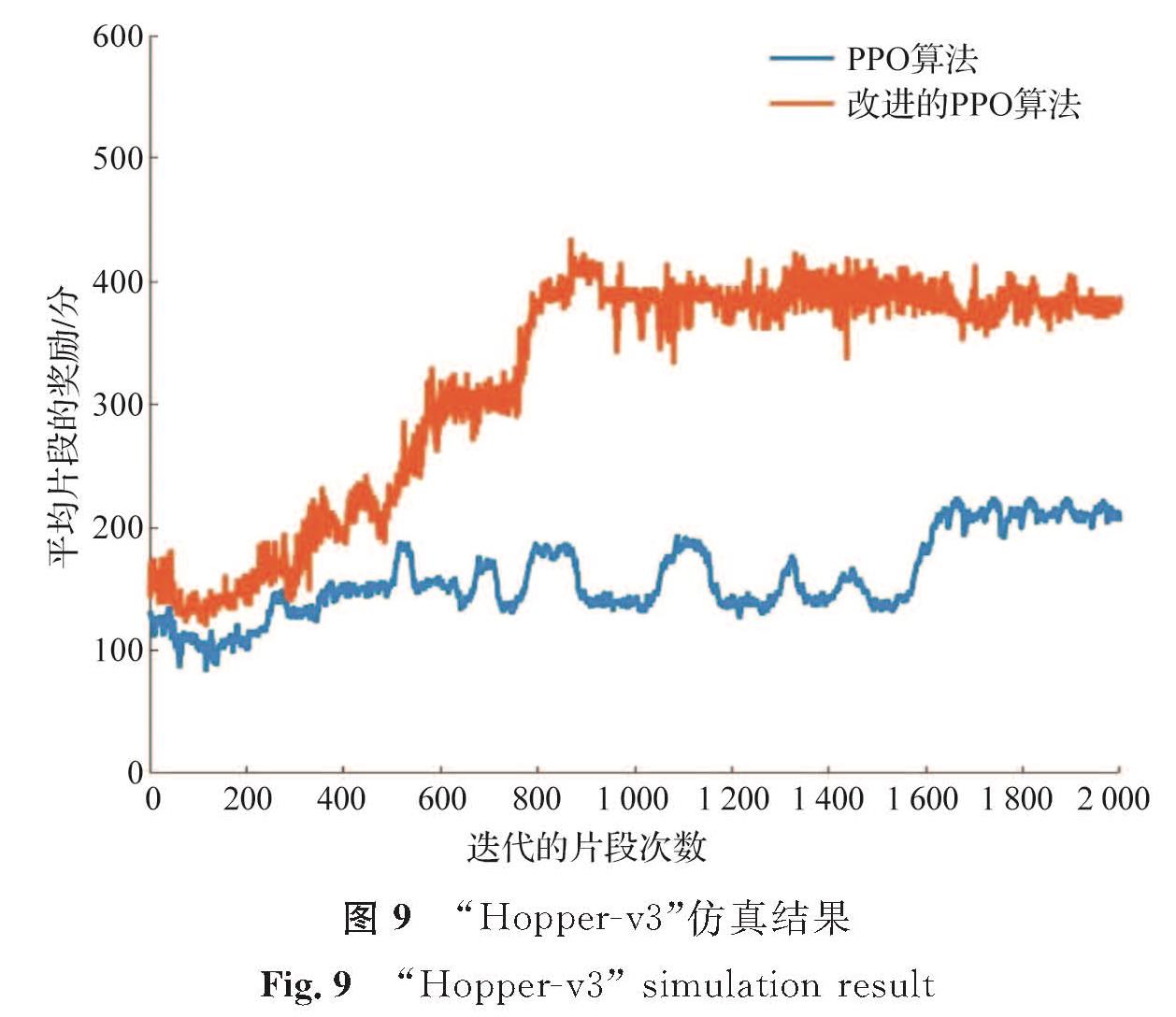
试验三:环境为mujoco模拟器中的“Hopper-v3”,其他参数的设置情况如下:最大迭代的片段次数为2 000,每个片段最大训练次数为200,动作限制在[-3,3]之间,模型经过2 000次迭代训练,其迭代的片段次数及平均片段的奖励如图9所示。

图9 “Hopper-v3”仿真结果<br/>Fig.9 “Hopper-v3” simulation result

图9 “Hopper-v3”仿真结果
Fig.9 “Hopper-v3” simulation result

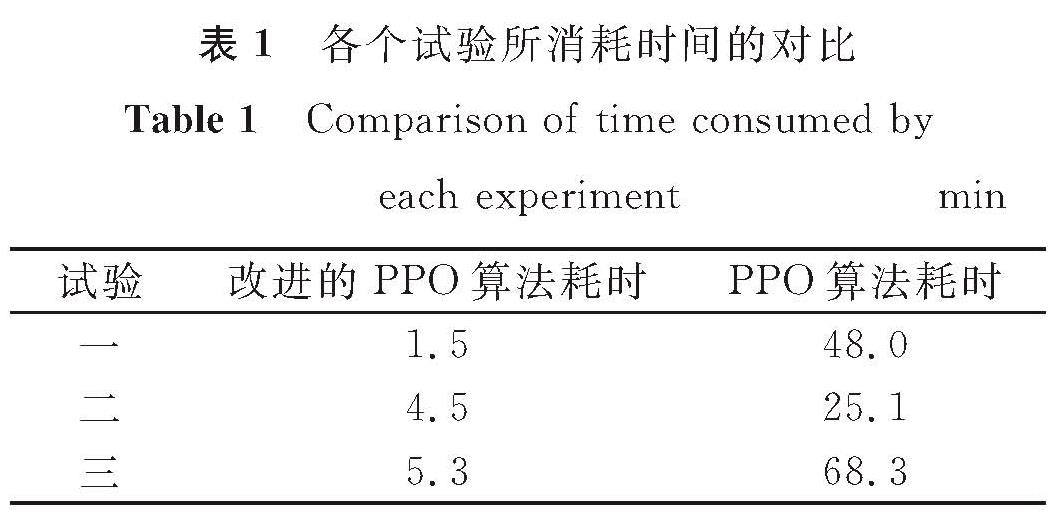
从图7可知,随着训练的迭代次数增加,改进的PPO算法图形(黄色曲线)会比PPO算法图形(蓝色曲线)更快趋于稳定,也就是获得更多的奖励,从而使钟摆更快地学会如何通过摆动来保持直立,且稳定后其收敛性会更好。在复杂的mujoco环境中这种优势会更加的明显。从图8可知,随着训练迭代次数的增加,黄色曲线比蓝色曲线更先趋于稳定,且其每个片段平均奖励更多。可见,改进的PPO算法使四足机器人能更快地学会行走,获得的奖励也更多。从图9可知:蓝色曲线在训练的过程中波动比较大,黄色曲线比蓝色曲线获得更多平均片段奖励,且其稳定性也更好。同理,单足机器人在改进的PPO算法中也能很快地学会向前跳跃,且在训练的过程中其收敛性比PPO算法更好。在试验中,改进的PPO算法与PPO算法训练智能体的过程所消耗时间的对比见表1。

表1 各个试验所消耗时间的对比
Table 1 Comparison of time consumed by each experimentmin

表1 各个试验所消耗时间的对比<br/>Table 1 Comparison of time consumed by each experimentmin

由表1可知,改进的PPO算法在参数相同的情况下,训练智能体的速度至少是PPO算法的5.5倍,最多是32倍。

4 结语

强化学习是一类重要的机器学习方法。为提升强化学习的算法效率,我们提出了一种改进的近端策略优化(PPO)算法:在更新网络参数θ的损失函数中的散度项上加了限制,优损失函数; 采取泛化优势估计作为优势函数的估计方式,平衡了偏差和误差给价值函数及回报带来的影响; 采用多线程的方式,加快了训练的效率; 在主副网络的参数更新方式上做了调整改进。改进的PPO算法与PPO算法均在gym环境中进行了仿真对比测试,结果表明改进的PPO算法会使智能体更快地学到经验,获得更多的奖励,且训练过程中收敛性更好。

参考文献

[1] 高阳,周如益,王皓,等.平均奖赏强化学习算法研究[J].计算机学报,2007,30(8):1372.
[2] GU S, HOLLY E, LILLICRAP T, et al. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates[C]//2017 IEEE International Conference on Robotics and Automation. Singapore: IEEE,2017:3389.
[3] FOERSTER J, ASSAEL I, DE FREITAS N, et al. Learning to communicate with deep multi-agent reinforcement learning[J].Advances in Neural Information Processing Systems,2016,29(3):2145.
[4] 刘全,翟建伟,章宗长,等,深度强化学习综述[J].计算机学报,2018,41(1):1.
[5] 杨霄,李晓婷.基于深度强化学习的自动驾驶技术研究[J].网络安全技术与应用,2021,1(1):136.
[6] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[EB/OL].[2021-07-05].
[7] SUTTON S, MCALLESTER D, SINGH S, et al. Policy gradient methods for reinforcement learning with function aproximation[J].Advances in Neural Information Processing Systems,1999,12:10.
[8] KONDA V, TSITSIKLIS J. Actor-critic algorithms[J].Advances in Neural Information Processing Systems,1999,12:173.
[9] 苏壮.基于路径的移动预测及路线规划研究[D].北京:北京邮电大学,2020.
[10] LILLICRAP T, HUNT J, PRITZEL A, et al. Continuous control with deep reinforcement learning[EB/OL].[2021-07-05].
[11] MNIH V, BADIA A, MIRZA M, et al. Asynchronous methods for deep reinforcement learning[C]//International conference on machine learning. Stockholm: PMLR,2016:1928.
[12] SCHULMAN J, LEVINE S, ABBEEL P, et al. Trust region policy optimization[C]//International conference on machine learning. Stockholm: PMLR,2015:1889.
[13] SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL].[2021-07-05].
[14] HEESS N, SRIRAM S. Emergence of locomotion behaviours in rich environment[EB/OL].[2021-07-05].
[15] SUTTON R, BARTO A. Reinforcement learning: an introduction[M].Cambridge: MIT Press,2018.
[16] 万里鹏,兰旭光,张翰博,等.深度强化学习理论及其应用综述[J].模式识别与人工智能,2019,32(1):67.
[17] 杜威,丁世飞.多智能体强化学习综述[J].计算机科学,2019,46(8):1.
[18] 郭峰.电商平台搜索广告的转化率提升研究[D].徐州:中国矿业大学,2019.
[19] WALTER J, BARKEMA G. An introduction to monte carlo methods[J].Physica A: Statistical Mechanics and its Applications,2015,418(1):78.