随着网页技术和虚拟现实技术的快速发展,基于Web3D[1]技术进行网页端虚拟现实开发越来越流行。WebGL(web graphics library,网络图形库)源于OpenGL ES 2.0(open graphics library for embedded systems 2.0,嵌入式系统开放图形库2.0)标准,可使用HTML5(hyper text markup language 5.0,超文本标记语言5.0)的Canvas元素作为DOM(document object model,文件对象模型)接口访问的一种实现Web交互式三维图形渲染技术[2-3],具有无插件、跨平台、可直接驱动硬件加速等优势[4]。WebGL因其上述优点受到广大厂商的支持,进一步衍生出一些优秀的渲染引擎,发展于WebGL的Babylon.js引擎因其强大的渲染功能已成为目前网页端虚拟现实开发选择的主流三维引擎[5-6],目前在Babylon.js等三维虚拟引擎中实现物体运动轨迹的规划要考虑重力、摩擦力等物理条件,才能在视觉上体现三维物体运动的真实性,实现起来较困难,会受到很多因素的干扰与制约。为简单高效地实现三维物体复杂的曲线运动轨迹,可在虚拟引擎中使用Bézier曲线提前绘制出合适的目标轨迹,再让物体沿此轨迹运动。在现实生活中,Bézier曲线已被运用于物体的路径规划中,Han等[7]提出了一种基于Bézier曲线的路径规划器,能形成最优避障路线,实现了汽车的防碰撞行为。杨彬等[8]运用三阶Bézier曲线对无人驾驶车辆起始点至终点之间的轨迹进行拟合,通过对Bézier曲线控制点参数进行合理的赋值,可实现对拟合轨迹的局部调整。Tharwat等[9-10]采用Bézier曲线的路径规划模型,实现了对移动机器人的最优平滑路径规划。已有一些研究将Bézier曲线应用于虚拟现实中,如孙晨阳[11]在虚拟现实中利用双三次Bézier曲面和多边形对小麦各个器官进行建模,可以以低成本和较高的效率模拟小麦生长过程,模型表面光滑且可以实现小麦不同生长期的建模; Wu等[12]将Bézier曲线算法与三维物体的网格顶点相结合,实现对三维物体的杆件弯曲。综上所述,将Bézier曲线运用于虚拟现实中三维物体的轨迹设计是可行的,但目前虚拟现实应用所涉及的曲线形状相对比较简单,只需通过固定阶次Bézier曲线即可实现绘制,灵活性较弱,且在Web3D技术上Bézier曲线应用极少。
通过物体运动原理及数学公式确定物体运动轨迹的方法给虚拟现实网页端开发人员的图形设计带来不便,其原因是:原理不易理解且参数过多; 复杂无规律轨迹使用数学公式也难以快速描述,且轨迹调整需重新进行计算。而Bézier曲线通过调节控制点的数量和位置就可快速完成轨迹的绘制与调整,故研究基于Babylon.js引擎对复杂轨迹进行可视化设计并进行运动仿真很有必要。目前,Babylon.js环境中仅有二阶和三阶Bézier曲线的实现方法,并没有设计任意阶次的实现方法。将Bézier曲线灵活应用于Babylon.js环境下的虚拟三维物体轨迹设计,需进行算法设计和Typescript编程,以最终实现对三维物体运动轨迹的可视化交互控制。为此,我们设计了一种基于Babylon.js的n阶Bézier曲线的绘制方法,可自定义中间控制点的数量和位置,从而实现三维物体复杂运动轨迹的绘制。
1 Bézier曲线定义法国工程师Pierre Bézier在1962年提出了一种通过连接向量来表示曲线的方法,这样的曲线被称为Bézier曲线。由于表达直观、结构简单,Bézier曲线是计算机辅助几何设计中表示曲线和曲面的重要工具[13],常被用来绘制复杂的图形形状[14]和模型样式[15]。使用Bézier曲线方法绘制曲线方便快速,只要给定曲线的起点和终点,然后通过调节中间点的数量及位置来控制曲率,就可得到目标曲线。
在空间中给定n+1个控制点Pi,i=0,1,2,…,n,则n阶Bézier曲线可描述如下:

式(1)中:t为独立变量; Bi,n(t)为第i个n阶Bernstein多项式,
Bi,n(t)=Cinti(1-t)n-i。(2)
Bézier曲线求导公式如下:
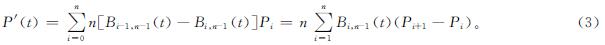
在绘制三维物体运动轨迹的实际应用中,针对不同需求往往需运用不同阶次的Bézier曲线,开发者只需改变函数中的参数即可绘制不同阶次的曲线轨迹,目前在Babylon.js环境中已实现二阶、三阶Bézier曲线轨迹的绘制,并封装为接口供用户使用,但其他阶次Bézier曲线还未实现。本研究给出一种n阶Bézier曲线运动轨迹自动生成方法,其核心思想是设计getBezierArr函数来生成以各控制点位置为基础的Bézier曲线轨迹; 其解决思路是设计一种循环递归的计算方法来完成Bézier曲线轨迹点的自动插值。首先,在基于WebGL网页端开发中,在Babylon.js环境下运用Typescript语言进行程序编写,以此实现getBezierArr函数的基本功能; 然后,在起点、终点和中间控制点相同的情况下,比较Babylon.js环境中采用BABYLON.Curve3.CreateQuadraticBezier和BABYLON.Curve3.CreateCubicBezier函数所生成的曲线与本文方法所生成的Bézier曲线的一致性; 再设计transformNode方法让小球沿所生成曲线轨迹运动,验证三维物体在所生成轨迹上运动的可行性; 最后,以getBezierArr函数的曲线拟合功能为基础,通过鼠标操作控制点位置,实时更新曲线轨迹的形状,以完成曲线的可视化交互设计。
2.2 函数设计使用getBezierArr函数获取组成Bézier曲线路径的插值线段点集合,它的参数为getBezierArr(ctrlPosArr:Array<BABYLON.Vector3>,precison:number)。ctrlPosArr表示由起点、终点和所有中间控制点组成的数组,precison表示通过多少个顶点来描述Bézier曲线,这些点随式(1)中参数t的变化依次均匀分布在Bézier曲线的路径上。
将式(2)进行变形:
Bi,n(t)=Cinti(1-t)n-i=(Cin-1+Ci-1n-1)ti(1-t)n-i=(1-t)Cin-1ti(1-t)(n-1)-i+tCi-1n-1ti-1(1-t)(n-1)-(i-1)=
(1-t)Bi,n-1(t)+tBi-1,n-1(t)。(4)
式(4)表明:n阶Bernstein多项式是n-1阶Bernstein多项式的线性组合,具有递归性。
把式(4)代入式(1)展开得:
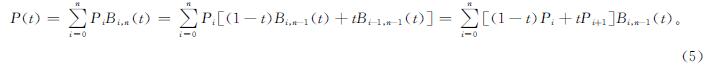
由此可推出Bézier曲线的递推公式如下:
P(t)=Pn0; (6)
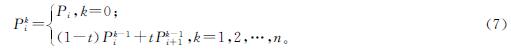
式(6)、(7)中:Pn0为首个n次Bézier曲线迭代多项式; Pki为第i+1个k次Bézier曲线迭代多项式,i=0,1,…,n-k。
Bézier曲线递推计算公式可理解为每相邻两个控制点插值出新的控制点,相邻的两个新控制点再插值出新的控制点,循环n次后得出最终的P(t)插值点,下面对一阶、二阶、三阶Bézier公式进行分析。
对一阶Bézier公式展开得
P10=P0(1-t)+P1t。(8)
对二阶Bézier公式展开得
P20=P0(1-t)2+P1×2(1-t)t+P2t2。(9)
逐级简化分解后得:

对三阶Bézier公式展开得
P30=P0(1-t)3+P1×3(1-t)2t+P2×3(1-t)t2+P3t3。(12)
逐级简化分解后得:
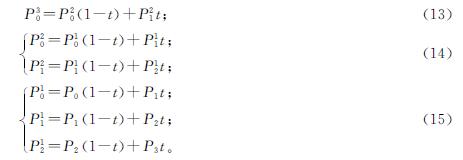
从一阶、二阶、三阶Bézier曲线的逐级简化分解公式推导可以发现,这是一个逐级循环递归的过程,每经过一次循环计算,控制点将会减少一个,直到最后只剩2个控制点,即可完成t时刻n阶插值点的计算。对n阶Bézier公式可利用计算机进行如下操作,先计算一阶的控制点P1i(n个),再计算二阶的控制点P2i(n-1个),经过n-1次逐级循环后计算n-1阶的控制点Pn-1i(2个),最后第n次循环计算出n阶的控制点Pn0。
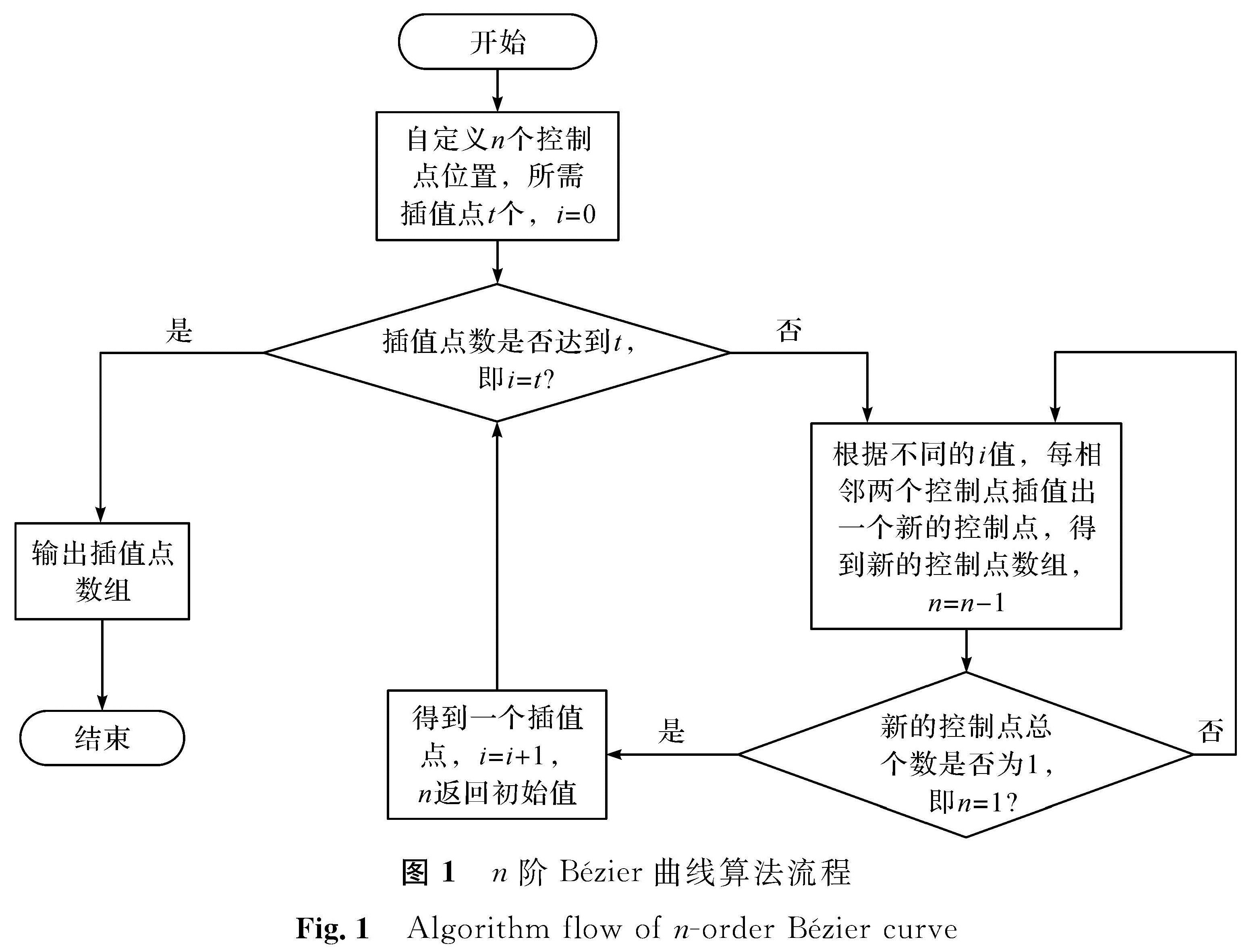
2.3 方法的实现不同场景中不同阶次Bézier曲线运动轨迹的使用都可通过以下步骤实现。首先,以循环递归的插值方法实现某一位置处插值点坐标值的求取; 然后,根据所需精度,即插值点的数量,依次计算轨迹上所有插值点的坐标值,形成一个Bézier曲线轨迹点集合; 最后,设置三维物体的位置,使物体依次经过轨迹点集合中的每个点。n阶Bézier曲线算法流程如图1所示。
3 试验与对比分析
在Babylon.js环境下,使用BABYLON.Mesh.CreateLines方法绘制Bézier曲线。CreateLines主要用于三维世界中线段的渲染,可在线段绘制时进行很多操作,比如设置宽度、颜色。在Babylon.js环境下对比采用本文方法生成的n阶Bézier曲线与内置方法生成Bézier曲线的一致性,来验证设计方法的正确性与稳定性。因为内置方法并没有实现n阶Bézier曲线的生成方法,只有CreateQuadraticBezier(二阶)和CreateCubicBezier(三阶)两种方法,所以本研究选择n=2、n=3时的n阶Bézier曲线生成方法与内置二阶、三阶进行对比; 最后与经典六阶Bézier曲线进行对比以验证本文方法高阶的有效性,为后续小球仿真试验做铺垫。对于三维空间中的一组顶点,CreateLines方法可使相邻两个顶点之间渲染生成一条直线,当顶点数量较多时,可生成一条相对平滑的曲线。因此,将getBezierArr方法计算出的曲线插值点坐标数组代入CreateLines中生成所需的目标曲线。
3.1 二阶Bézier曲线对比当n=2时,设置相同的顶点数和Bézier曲线控制点集合,然后将本文getBezierArr方法与内置Create-QuadraticBezier方法进行对比,为了有明显的视觉对比效果,设置了不一样的曲线样式。二阶Bézier曲线试验参数见表1。通过表1的点集绘制生成二阶Bézier曲线,本文getBezierArr方法用绿色线条,内置CreateQuadraticBezier方法用一系列连续的点表示,二阶Bézier曲线轨迹效果对比如图2所示。
3.2 三阶Bézier曲线对比
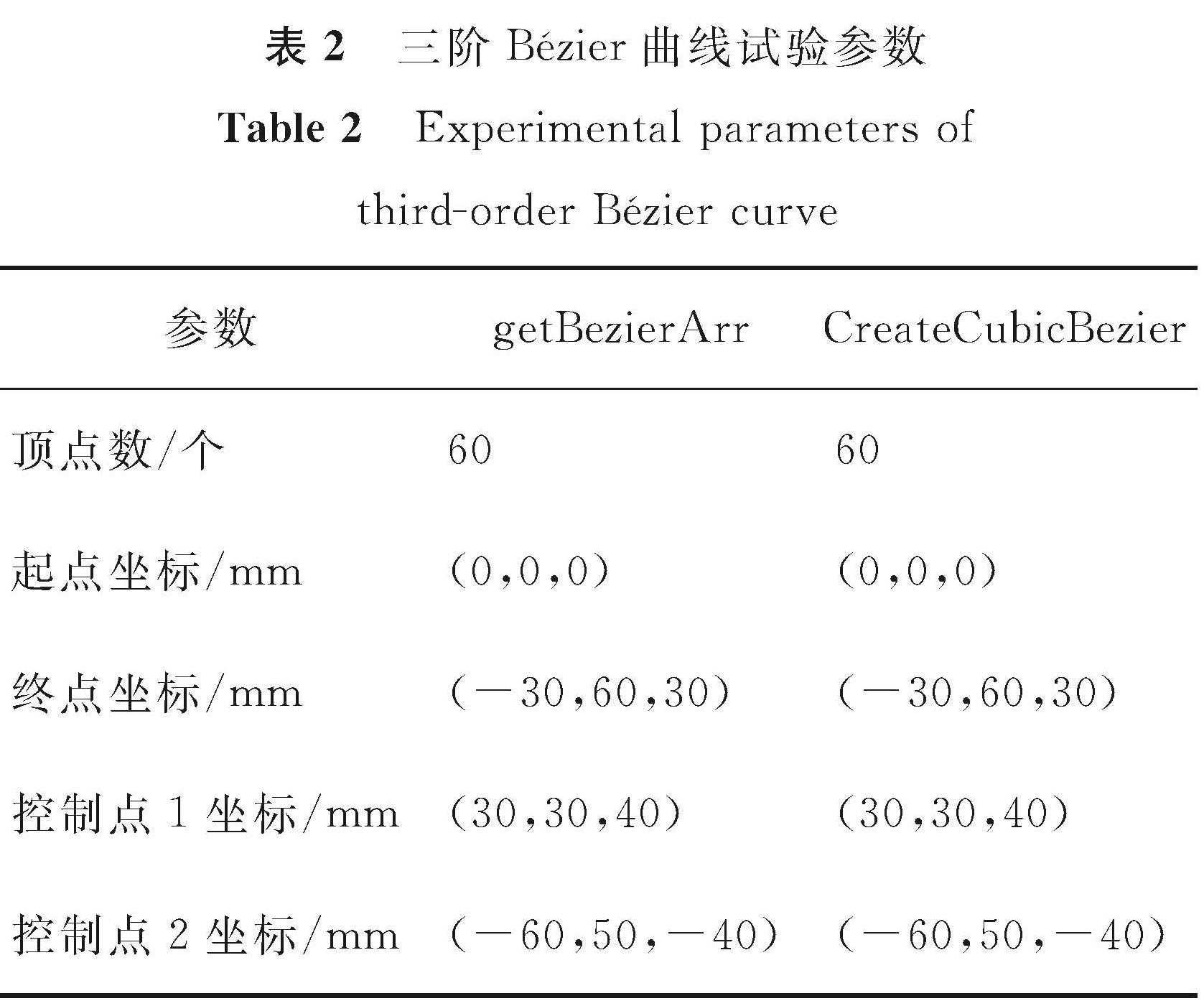
当n=3时,设置相同的顶点数和Bézier曲线控制点集合,将本文getBezierArr方法与内置CreateCubicBezier方法进行对比,三阶Bézier曲线试验参数见表2。通过表2的点集绘制生成三阶Bézier曲线,本文getBezierArr方法用绿色线条,内置CreateCubicBezier方法用一系列连续的点,三阶Bézier曲线轨迹效果对比如图3所示。
3.3 高阶Bézier曲线对比
以n=6为例,验证本文getBezierArr方法对高阶Bézier曲线生成的有效性。由式(1)可得出六阶Bézier曲线计算公式如下:
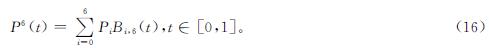
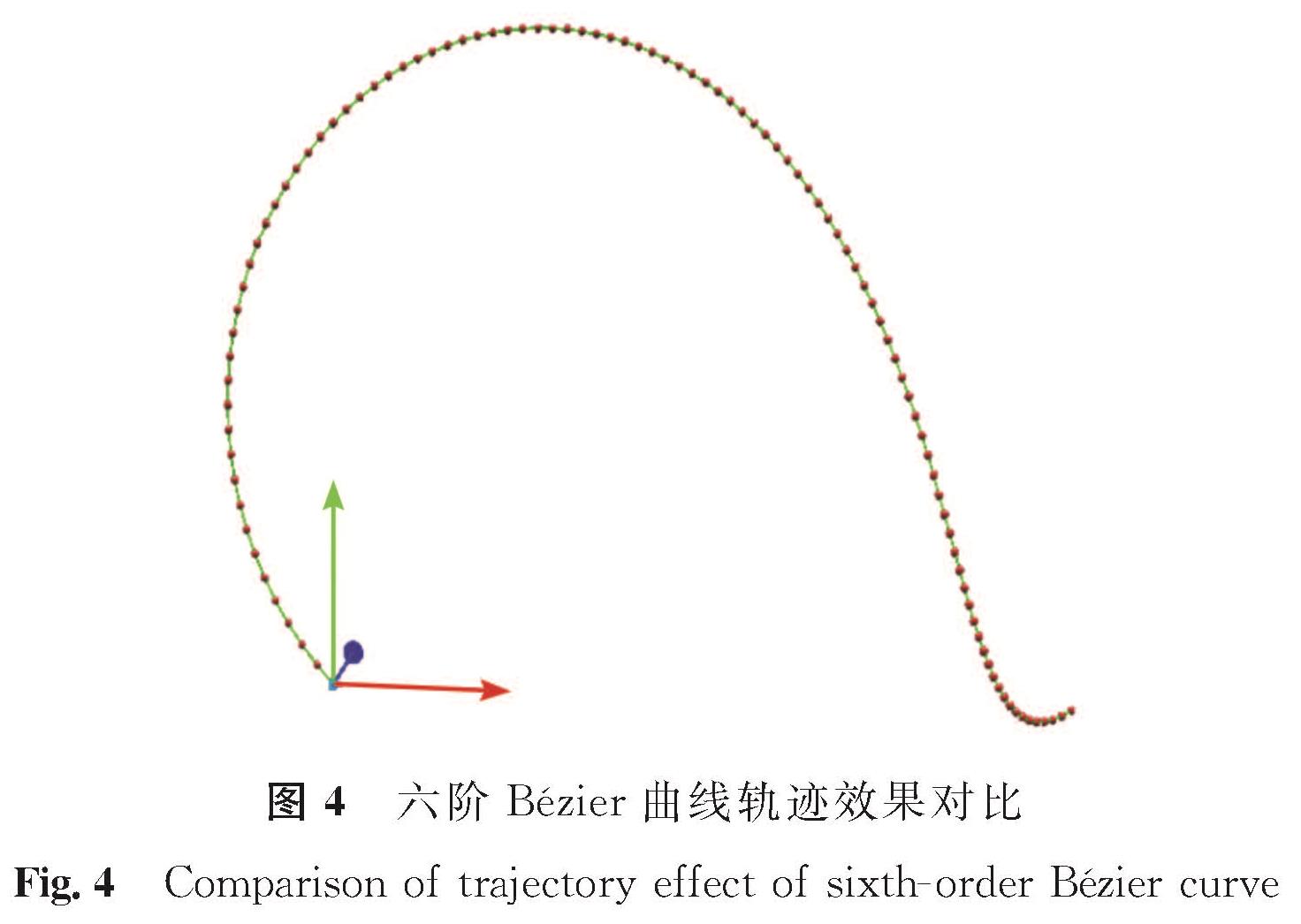
以式(16)为理论基础,可实现经典的六阶Bézier曲线拟合算法,绘制函数为CreateSixBézier。设置相同的顶点数和Bézier曲线控制点集合,与本文getBezierArr方法进行对比,六阶Bézier曲线试验参数见表3。通过表3的点集绘制生成六阶Bézier曲线,本文getBezierArr方法用绿色线条,CreateSixBézier方法用一系列连续的点,六阶Bézier曲线轨迹效果对比如图4所示。
3.4 试验对比结果
在起点、终点、中间控制点一致的情况下,Babylon.js环境下本研究Bézier曲线形成方法与经典二、三阶和六阶Bézier曲线算法所形成的运动轨迹完全重合,验证了本研究n阶Bézier曲线形成方法在低阶和高阶上的有效性,从而为下一阶段小球沿n阶Bézier曲线轨迹运动仿真试验与曲线形状可视化交互设计打下基础。
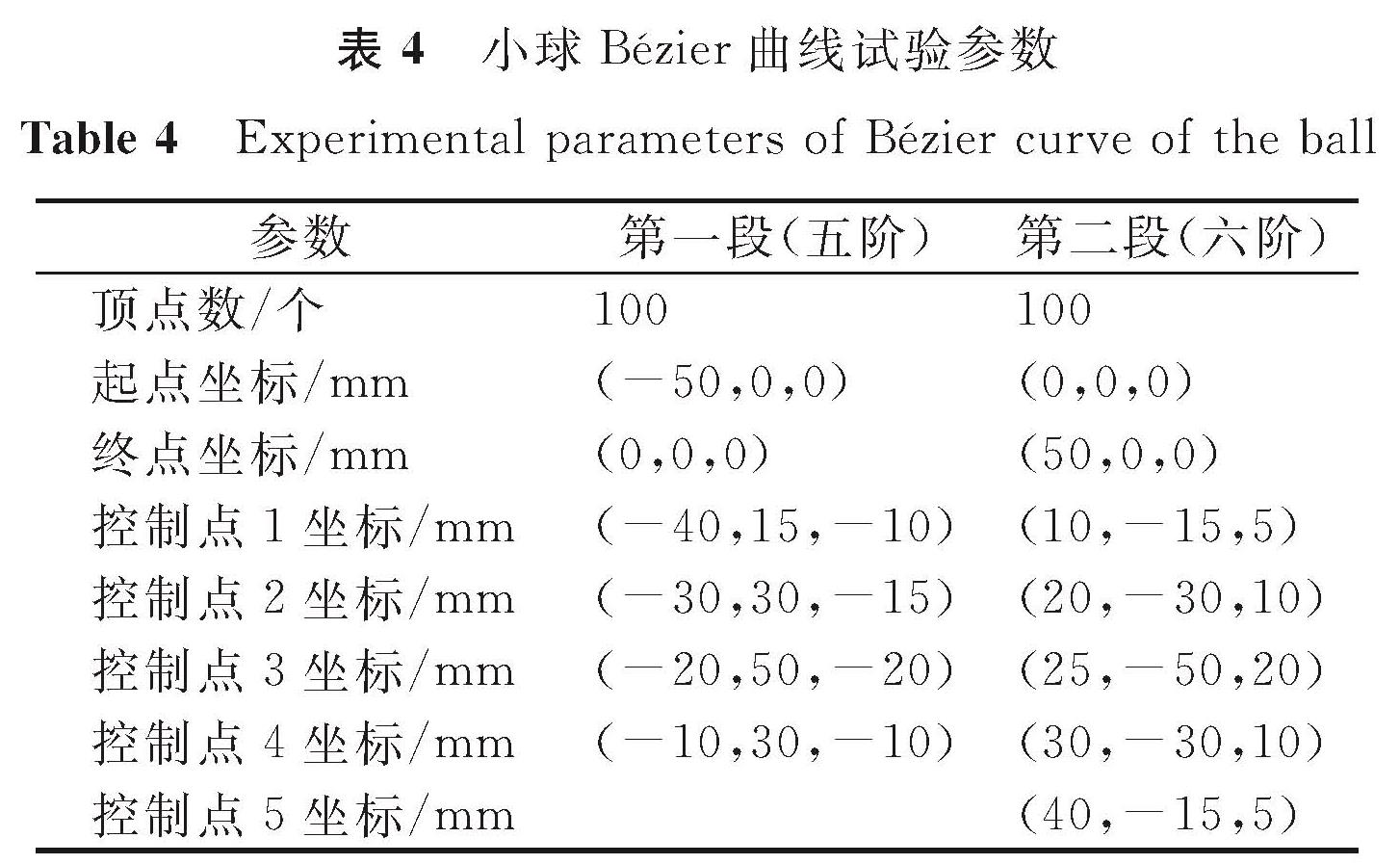
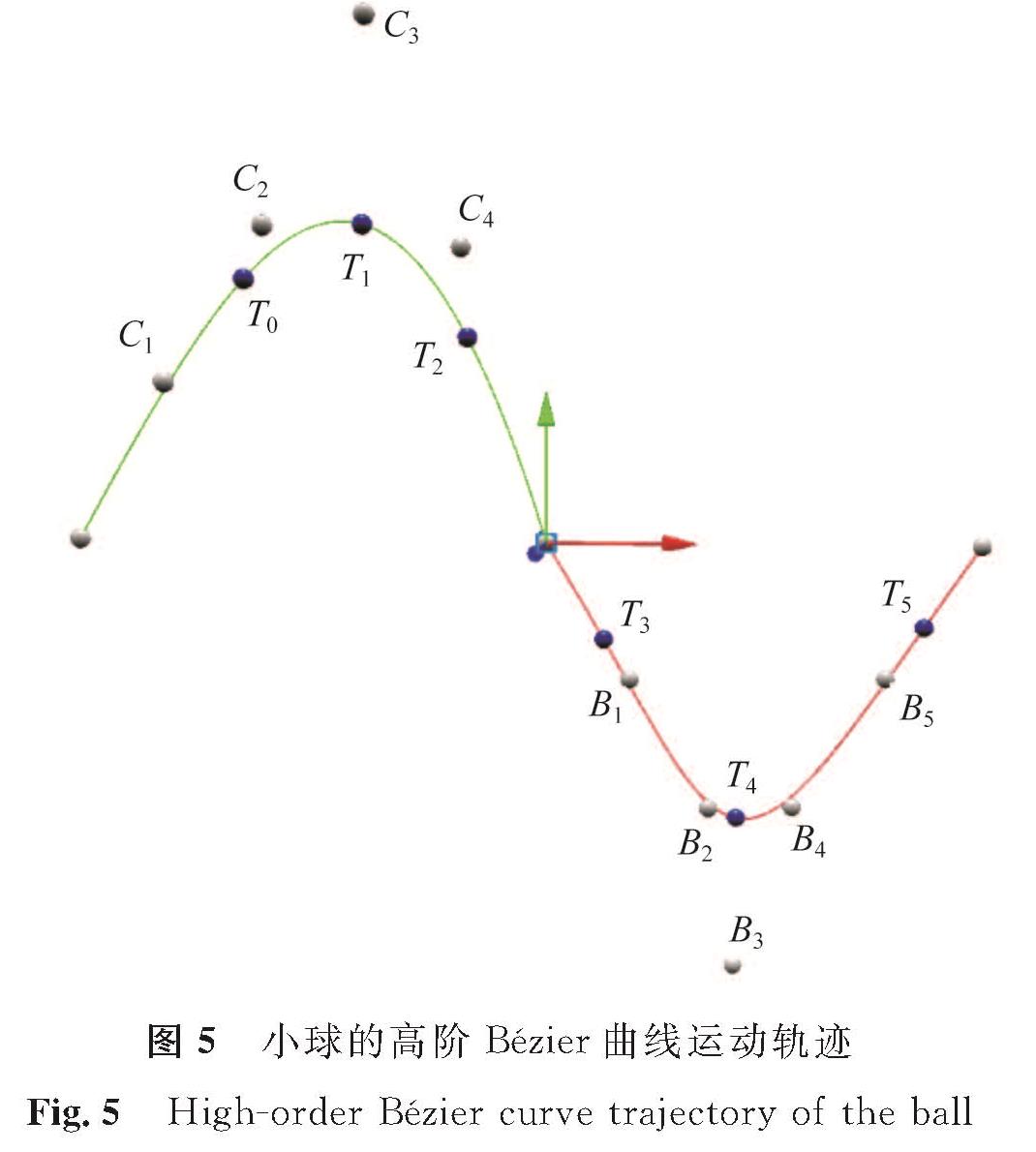
4 仿真试验4.1 仿真试验设计在Babylon.js环境中设计transformNode方法使小球沿所形成的Bézier高阶曲线路径运动,transformNode方法能改变物体的三维坐标,如果此方法刷新较快的话,就会在视觉上形成物体移动的效果。由式(1)~(3)可知,Bézier阶数越高,则曲线上各点的可导阶数更高,曲线连续性更强,曲线更光滑,物体的运动视觉效果肯定更好,但要调整的点比较多; 因此,可针对不同情况采取合适的阶次,在需要光滑度较高的地方可采用高阶次Bézier曲线设计,精度要求不高的地方可采取低阶Bézier曲线设计。为实现不同高阶的小球模拟和可视化操作效果,在此通过getBezierArr方法生成一个由两段高阶Bézier曲线组成的小球轨迹图,第一段为五阶,第二段为六阶,然后让小球沿此路径移动,观察小球是否能沿此路线运动。首先设置每段的起点和终点坐标,为实现连续运动,让第一段的终点和第二段的起点坐标相同,第一段设计4个中间控制点,第二段设计5个中间控制点的位置坐标,小球Bézier曲线试验参数见表4。首先通过本文方法拟合出一条三维弯曲轨道; 然后在Babylon.js的playground中运用transformNode组件方法使小球沿所形成的Bézier高阶曲线路径运动; 最后设计曲线轨迹的调整控制方法,当鼠标光标位于某个控制小球上方时,就会触发该控制点的三维坐标轴,长按鼠标左键选取某个轴就可对该轴方向的控制点坐标进行调整,松开鼠标左键时根据新的控制点坐标计算出新的Bézier曲线轨迹点,绘制出新的三维轨迹。
通过表4中的第一段控制点C1、C2、C3、C4和第二段控制点B1、B2、B3、B4、B5成功绘制小球的高阶Bézier曲线运动轨迹,如图5所示,也通过transformNode方法成功实现了两段小球的平滑曲线运动,如图中T0、T1、T2、T3、T4、T5处的小球轨迹点所示。
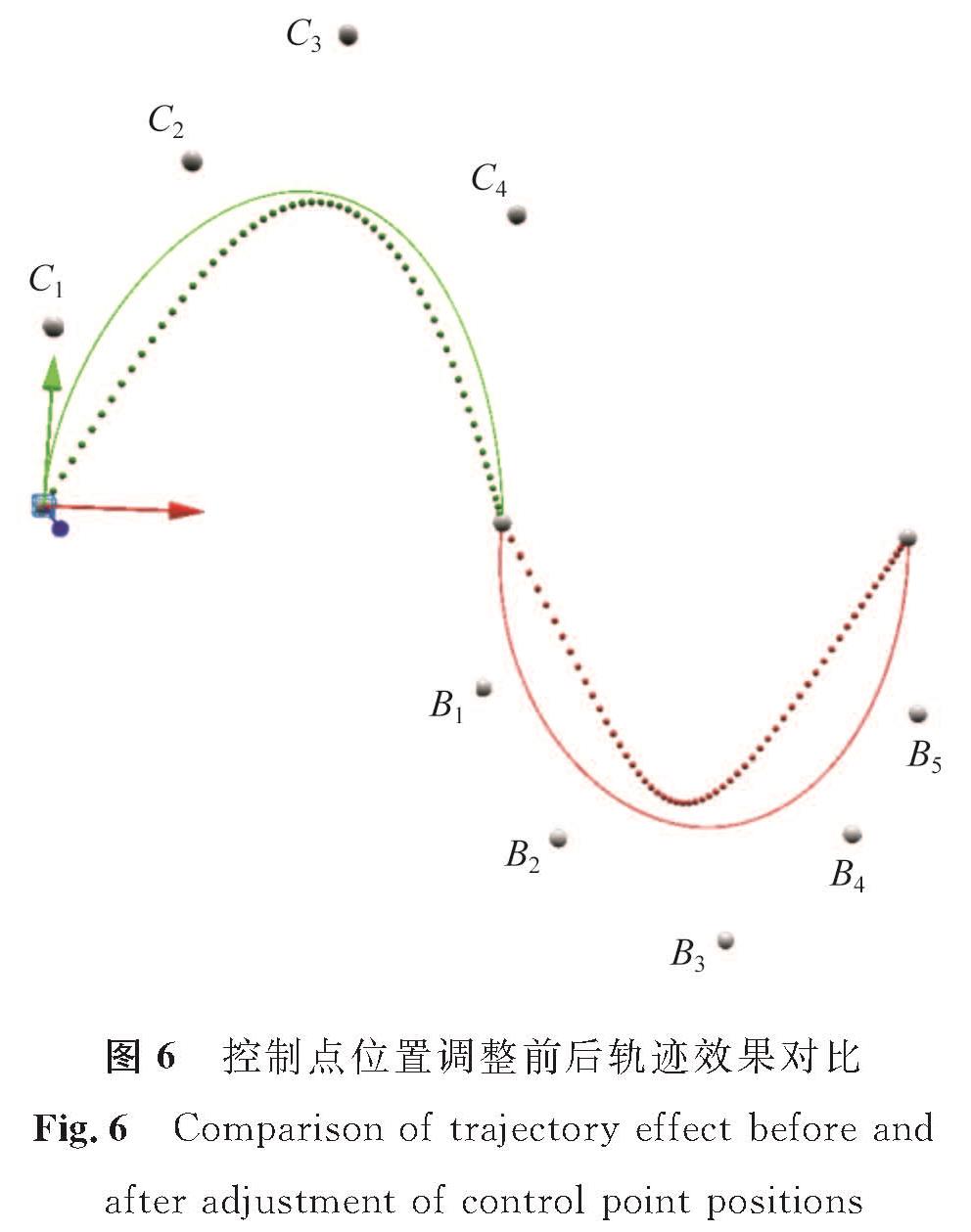
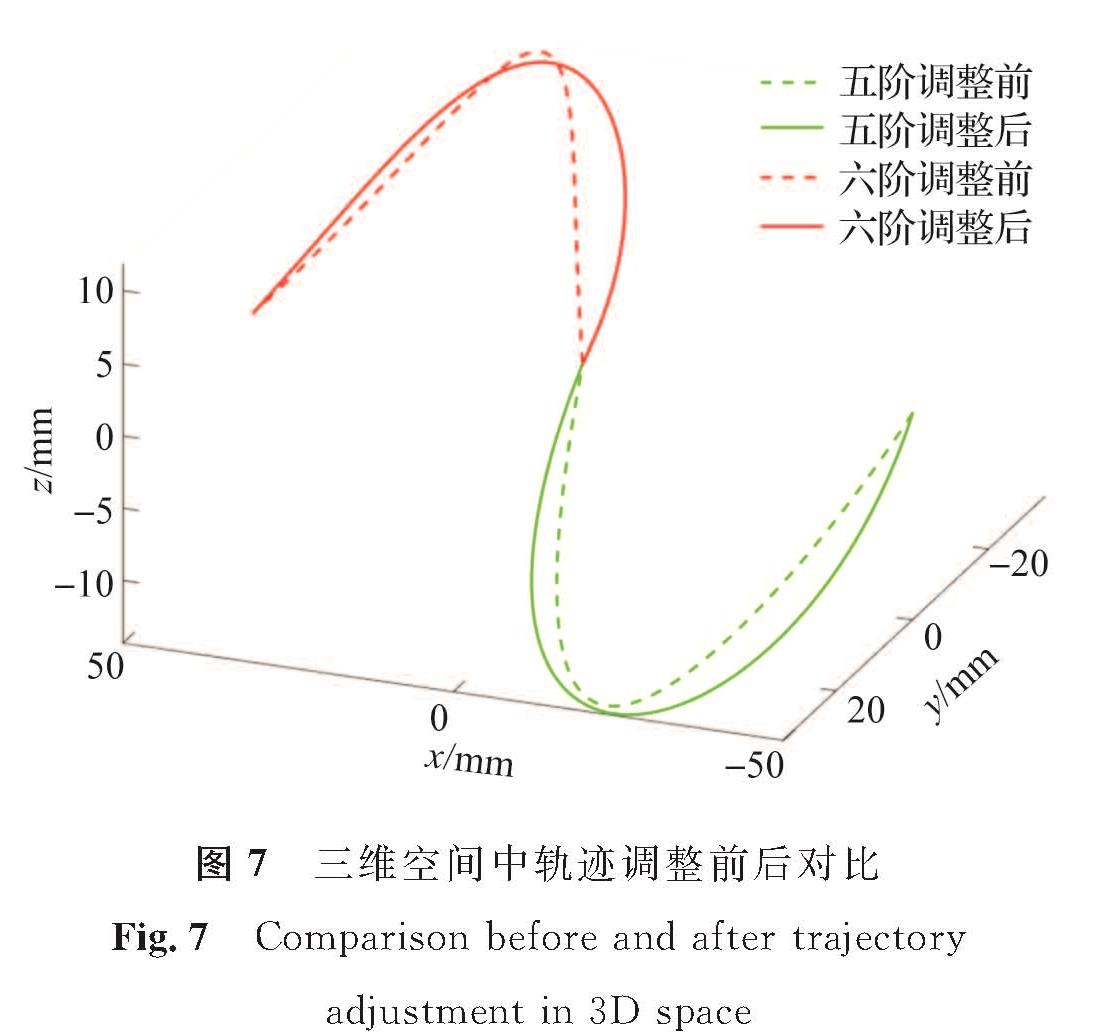
在图5的基础上,使用鼠标对图5中第一段控制点C1、C2、C3、C4和第二段控制点B1、B2、B3、B4、B5的坐标值进行拖拽调整,每拖拽一次就实时改变曲线的形状,实现可视化交互操作,最终实现沿目标轨迹曲线运动的效果。Babylon.js三维场景下,绿色线条为五阶Bézier曲线,红色线条为六阶Bézier曲线,点状线为控制点位置调整前所生成曲线效果,实线为调整后曲线效果,控制点位置调整前后轨迹效果对比如图6所示。将调整前后插值点数据导入MatLab中,生成三维坐标效果图,轨迹调整前后对比如图7所示。
图6 控制点位置调整前后轨迹效果对比
Fig.6 Comparison of trajectory effect before and after adjustment of control point positions
4.2 仿真结果
图5中,小球可以围绕生成的两段高阶Bézier曲线轨迹运动,证明了本文方法运用于三维物体轨迹生成的有效性。从图6和图7中的三维曲线绘制结果可知,一些复杂曲线轨迹可通过本文方法快速实现,只需改动控制点位置就可快速调整并绘制出整条轨迹,且对于不同阶次的Bézier曲线都能有效进行调整,从而实现了轨迹形状的可视化交互操作。
5 结 语本研究提出一种基于Babylon.js的任意阶Bézier曲线生成方法来设计网页端三维物体的运动轨迹。在Babylon.js环境下进行小球两段高阶Bézier曲线运动仿真,证明本文方法能很好地生成复杂的三维物体运动轨迹,通过鼠标可对不同阶次Bézier曲线轨迹形状进行可视化交互操作,简化了开发人员的工作量,提高了工作效率,也为应用Bézier曲线去规划基于网页端的三维物体运动轨迹提供了参考。
- [1] 王磊,高珏,金野,等.基于Web3D无插件的三维模型展示的研究[J].计算机技术与发展,2015,25(4):217.
- [2] 李琨,贾立伟,石晓明.基于WebGL技术的医学虚拟实验室的设计与实现[J].电脑知识与技术,2017,13(23):202.
- [3] 马亮,王彬,龚强,等.WebGL 3D技术及其在高校B/S系统中的应用研究[J].电子测试,2021(17):69.
- [4] 何珊,卿粼波,何小海,等.基于WebGL的岩心图像的三维重建及应用[J].现代计算机,2017(20):73.
- [5] MOREAU-MATHIS J. Babylon.js Essentials[M].Birmingham: Packt Publishing Ltd,2016:127.
- [6] SHEPILIEV D S, MODLO Y O, YECHKALO Y V, et al. WebAR development tools: an overview[J].CEUR Workshop Proceedings,2020,2832:84.
- [7] HAN L, YASHIRO H, NEJAD H T N, et al. Bezier curve based path planning for autonomous vehicle in urban environment[C]//2010 IEEE intelligent vehicles symposium.La Jolla: IEEE,2010:1036.
- [8] 杨彬,宋学伟,张勇,等.模拟驾驶人行为的无人驾驶车辆避障轨迹规划[C]//2021中国汽车工程学会年会暨展览会.上海:中国汽车工程学会,2021:170.
- [9] THARWAT A, ELHOSENY M, HASSANIEN A E, et al. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm[J].Cluster Computing,2019,22(2):4745.
- [10] SONG B, WANG Z D, ZOU L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve[J].Applied Soft Computing,2021,100(1):106960.
- [11] 孙晨阳.小麦生长的三维可视化建模方法研究[D].郑州:郑州大学,2019.
- [12] WU X L, HUANG X N. Using Bézier curve to bend 3D objects in unity[J].Modern Computer,2016,7(15):1.
- [13] 施法中.计算机辅助几何设计与非均匀有理B样条:CAGD & NURBS[M].北京:北京航空航天大学出版社,1994:121.
- [14] 张颖,练章华.基于Bezier曲线的特殊螺纹密封面参数化设计[J].中国安全生产科学技术,2019,15(11):24.
- [15] 孔令德,康凤娥.基于双三次Bezier曲面在球体建模中的应用[J].计算机应用与软件,2017,34(5):86.
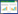 图 1 n阶Bézier曲线算法流程
Fig.1 Algorithm flow of n-order Bézier curve
图 1 n阶Bézier曲线算法流程
Fig.1 Algorithm flow of n-order Bézier curve