钻孔灌注桩因具有单桩承载力高、施工方便,且桩长和直径可按设计要求进行变化等特点,在地基基础工程中被广泛应用。但由于桩孔中存在浮浆层,导致钻孔灌注桩的施工过程无法被准确观测。在施工中,由于最上层存在混凝土和泥浆混合的浮浆层,所以最后一次灌注时要求灌注到标高以上,以确保桩头部分的质量合格,保证灌注桩的承载力。如果超灌量过多,会导致人力物力的浪费,超灌1 m³混凝土费用增加300元以上; 如果未灌注到标高,或出现标高以下的桩体质量不达标的情况,需要采取接桩等手段进行二次施工,甚至可能需要整桩破除重新灌注,则造成的浪费更大。但是在混凝土灌注过程中,由于施工条件的限制,一般依靠施工人员的经验和在灌注现场的简易手工检测手段来估测超灌高度是否处于合理的范围,这样不但影响施工效率,耽误时间,也不能准确判断实际超灌高度。JGJ 94—2008 《建筑桩基技术规范》^[1]中提到,灌注桩应该对最后一次灌注量进行控制,超灌高度宜在0.8～1.0 m,但并未提及在更多的超灌量情况下对桩体产生的影响,尤其是对桩体位移的影响。而桩体位移与桩身承载力具有重要的关联性,因此研究不同土体中超灌量对桩体位移情况的影响具有一定的现实意义。

国内外许多研究者在混凝土灌注桩的承载力方面进行了不懈的探索。Andersen等^[2]定义了循环剪切强度这一术语,说明了该强度和土壤破坏类型与平均剪切应力之间的关联性。Rausche等^[3]提出了一种动态测量锤击下的力和加速度的方式,并推导出了计算桩贯入阻力的基本方程。王曙光等^[4]给出了针对螺杆型灌注桩的单桩极限承载力的表达式。刘开富等^[5-7]结合实际工程,通过在钻孔灌注桩的桩端、桩侧进行后注浆对土体进行加固,提高了单桩承载力,有效减少了桩的沉降。万志辉等^[8]建立了大直径后压浆桩的承载力和沉降的计算方法,并给出了部分参数的取值范围。周志良等^[9]以紧邻运营地铁S8线的南京龙津津桥改建工程为背景,发现近隧桩基施工对既有地铁隧道的影响主要集中于成孔阶段。吕军^[10]探讨了非均质地基中桩在竖向荷载作用下的承载特性,利用平衡原理和剪切位移法建立了桩身控制方程。杨建平等^[11]通过水平荷载对灌注桩桩体变形影响的研究,给出了特定情况下的弯矩计算公式。聂立武等^[12-13]通过数值模拟,发现超灌量的增加会导致桩体的竖向位移增大。张鑫等^[14]对比两个地质条件相似的工程,研究发现桩端土的类型会对承载力产生较大的影响。蔡楚辉^[15]依托广州南沙新区明珠湾区工程,对水利项目中的灌注桩群桩基础的施工工艺进行了改进。祝宏文^[16]分析发现钻孔内泥浆密度对超灌高度控制的精确性影响较大。谭海洲^[17]建立灌注桩侧摩阻力计算模型,分析黏性土中钻孔灌注桩承载性能的影响因素。高浩雄^[18]以围垌大桥为例,对成孔过程中的各类问题分别提出了相应的应对措施。

上述研究的主要方向集中在桩的竖向承载力、侧摩阻力、桩身沉降等方面,针对不同超灌量情况下的桩体位移情况研究较少,因此有必要对这方面的问题进行深入的研究。

超灌量指在标高之上灌注的混凝土量。在灌注桩实际施工过程中,桩身灌注混凝土的顶面存在泥浆与混凝土的混合物浮浆层,为了避免浮浆层对桩体质量产生影响,需要保留一定的超灌量。但是由于灌注过程中桩顶设计标高的混凝土面一般处于地下数米至十数米的区域,故无法直接对超灌高度进行准确观测。

现场简易手工检测方法指使用钢筋棍伸入桩孔,利用钢筋棍从浮浆或泥浆碰触混凝土时的手感变化来判断混凝土是否达到标高。这样的检测方法往往存在较大的误差,虽然它在一定的程度上避免了灌注不到位的欠灌情况发生,但是无法避免超灌量过大时导致的混凝土浪费现象。

由于钻孔灌注桩成孔的过程中存在塌孔等因素的影响,桩孔的孔径尺寸与设计直径难免会有出入,所以也无法通过计算灌注的混凝土量来准确判断混凝土面是否达到预定标高的位置。为了避免简易手工操作产生的误差和不准确性,人们研制了超灌监测仪器,其方法一般是将传感器放置到桩顶标高的位置,利用混凝土和浮浆的电阻、密度等不同介质物理性质或者利用混凝土和泥浆内部的压力和温度的不同,通过仪器的反馈来判断混凝土是否达到标高位置,并由仪器进行提示,帮助施工人员控制超灌高度。相比传统的人工检测方法,使用超灌监测仪器控制超灌高度的精确性和可靠性相对更高。

本研究采用有限元软件Midas GTS NX模拟灌注桩在素填土、粉质黏土及黏土中的受力情况和位移情况,桩体采用各向同性的弹性模型,桩周土体采用各向同性的Mohr-Coulomb模型。有限元划分网格采用混合网格生成器并匹配相邻面,生成网格化的六面体,并对灌注桩桩身位置和靠近桩身部分土体的网格进行了加密处理,以提高数值模拟结果的准确性。

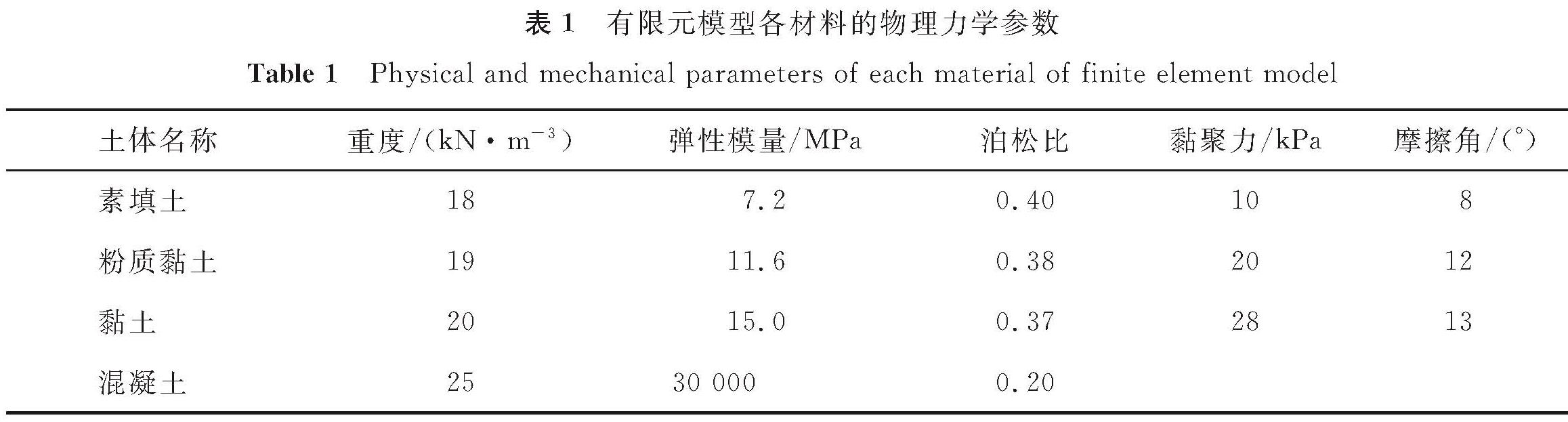
有限元模型参数如下:桩长为20 m; 桩径为0.8 m; 模型整体尺寸为40 m×40 m×40 m。有限元模型各材料的物理力学参数见表1。

表1 有限元模型各材料的物理力学参数
Table 1 Physical and mechanical parameters of each material of finite element model

图1 有限元及网格划分示意
Fig.1 Schematic diagram of finite element meshing

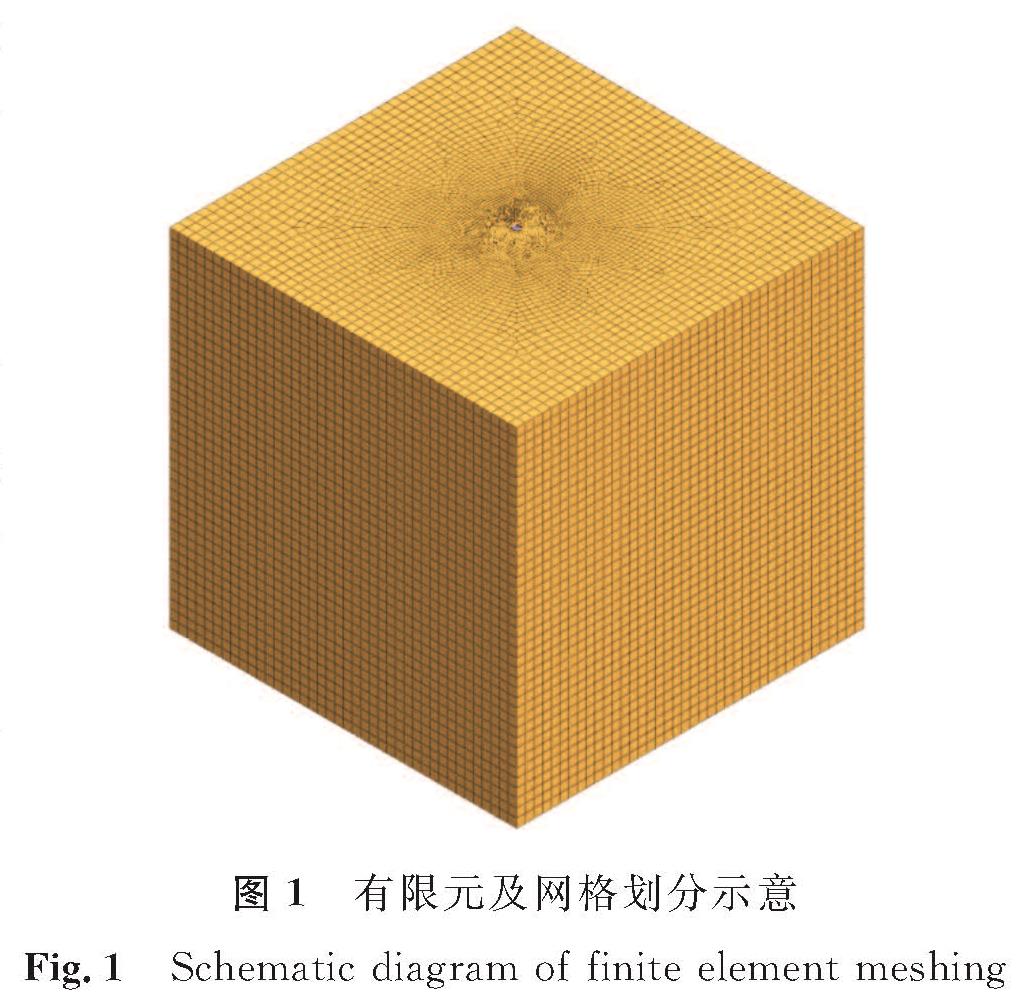
为了研究超灌量对桩体位移的影响,分别在不同的土体条件下建立混凝土灌注桩的有限元数值分析模型。上部为自由边界,底部设置全约束边界,各侧边约束限制对应方向的水平位移。为了更好地反映实际施工过程,对模型设置了3个施工阶段,分别是初始阶段、成桩阶段和加载阶段。在初始阶段将土体自身的沉降位移清零; 在成桩阶段,将设计桩孔内部的土体置换为混凝土桩体并添加相应的超灌层; 在加载阶段综合考虑泥浆层造成的荷载,对桩顶施加2 000 N/m²的均布荷载作为设计荷载。有限元及网格划分示意如图1所示。

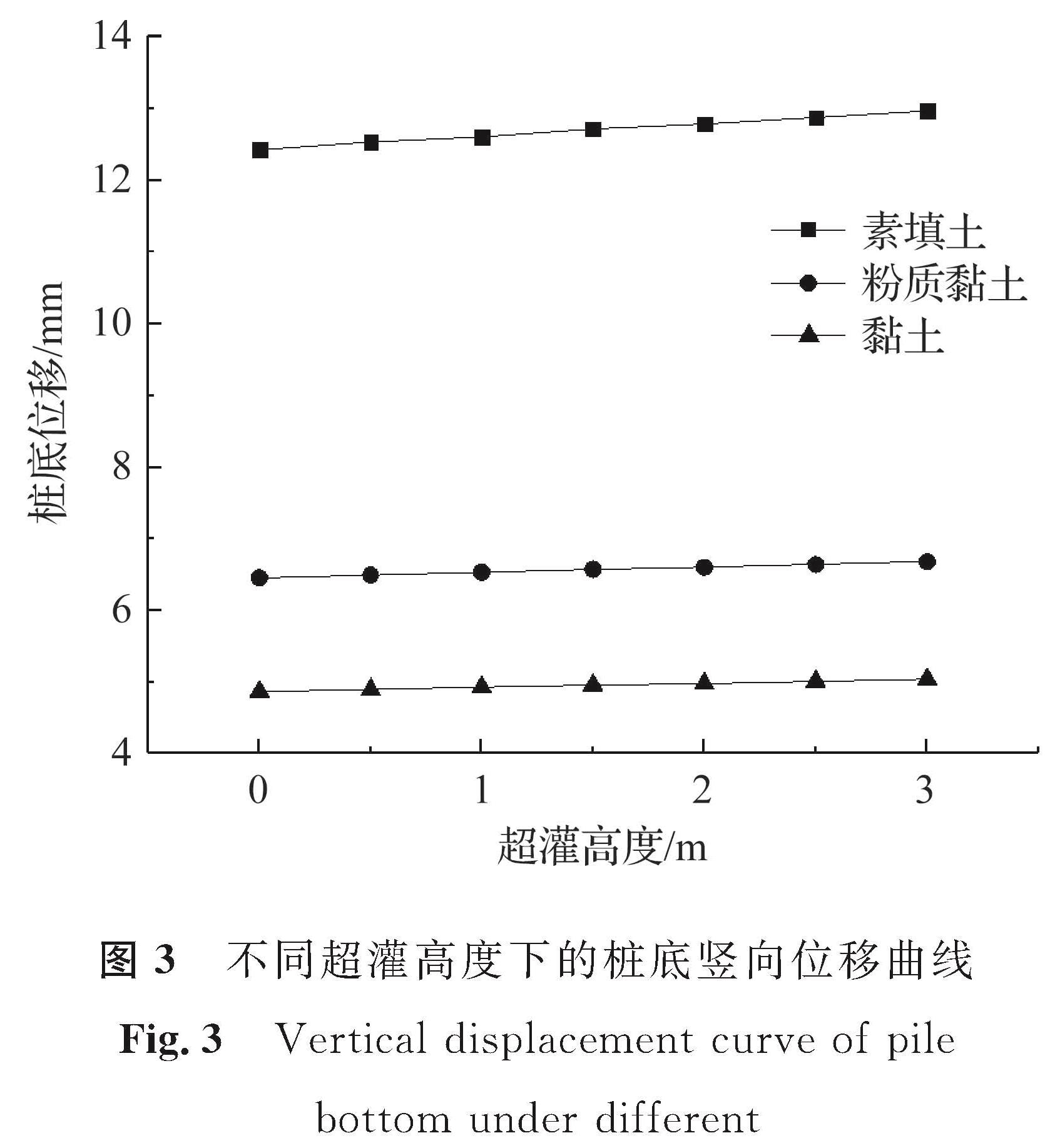
在模型的桩体上设置分别为0、0.5、1.0、1.5、2.0、2.5、3.0 m的超灌高度,得到在不同土体条件下的超灌桩体位移有限元分析模型。

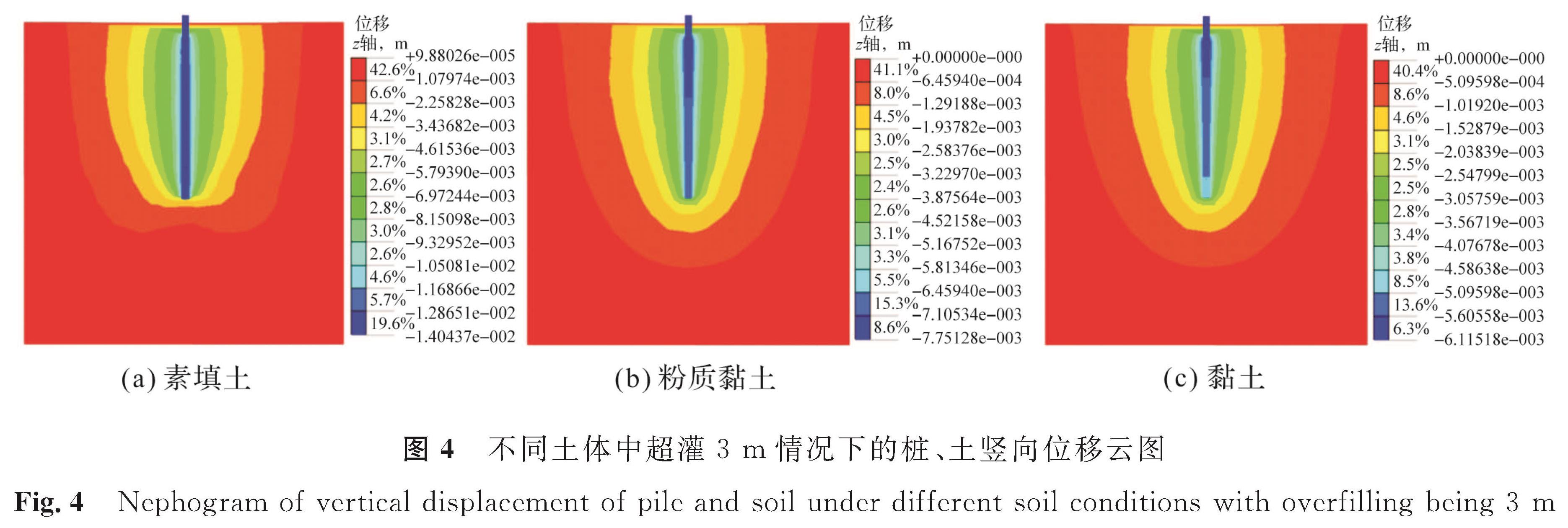
图2、图3分别为灌注桩的桩、土竖向位移云图和不同超灌高度下的桩底竖向位移曲线。在素填土中,超灌量从0 m增加到3 m时,桩底的竖向位移从12.43 mm增加到12.97 mm; 在粉质黏土中,超灌量从0 m增加到3 m时,桩底的竖向位移从6.45 mm增加到6.68 mm; 在黏土中,超灌量从0 m增加到3 m时,桩底的竖向位移从4.87 mm增加到5.04 mm。在3种土体中桩底的竖向位移均可看作随超灌量的增加而线性增长。相比粉质黏土和黏土,在素填土中,桩体位移整体上更大,随超灌量增加的位移变化也更加明显。不同土体中超灌3 m情况下的桩、土竖向位移云图如图4所示,桩体由于自重和上部施加的均布荷载,使桩体产生向下的位移。图4(a)为素填土、超灌3 m的情况下,桩底竖向位移12.97 mm; 图4(b)为粉质黏土、超灌3 m情况下,桩底竖向位移6.68 mm; 图4(c)为黏土、超灌3 m情况下,桩底竖向位移5.04 mm。桩身整体的沉降由桩身的压缩和桩底位移两部分组成,从桩体上下部分的位移对比可以看出,桩身压缩量很小,桩身整体沉降发生的主要原因是桩底位移的存在。同时在图2和图4中也可以看到,桩周土体的沉降情况:越靠近桩体的部分土体发生的竖向位移越大; 越接近桩体底部的土体竖向位移变化越快。

图2 桩、土竖向位移云图
Fig.2 Vertical displacement nephogram of pile and soil

图3 不同超灌高度下的桩底竖向位移曲线
Fig.3 Vertical displacement curve of pile bottom under different

图4 不同土体中超灌3m情况下的桩、土竖向位移云图
Fig.4 Nephogram of vertical displacement of pile and soil under different soil conditions with overfilling being 3m

考虑到桩侧土体的侧向位移近似于Mohr-Coulomb土体中的无限大土体中小孔扩张的特殊问题,以黏土中桩体超灌3.0 m的情况为例,根据小孔扩张理论进行计算。

Mohr-Coulomb屈服条件可用平面内主应力σ₁、σ₃表示为

1/2(σ₁-σ₃)=Ccosφ+1/2(σ₁+σ₃)sinφ。 (1)

整理得到:

式(1)～(2)中:C为黏聚力; φ为内摩擦角。

定义系数如下:

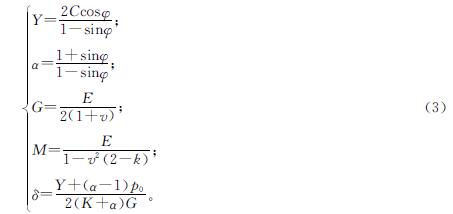
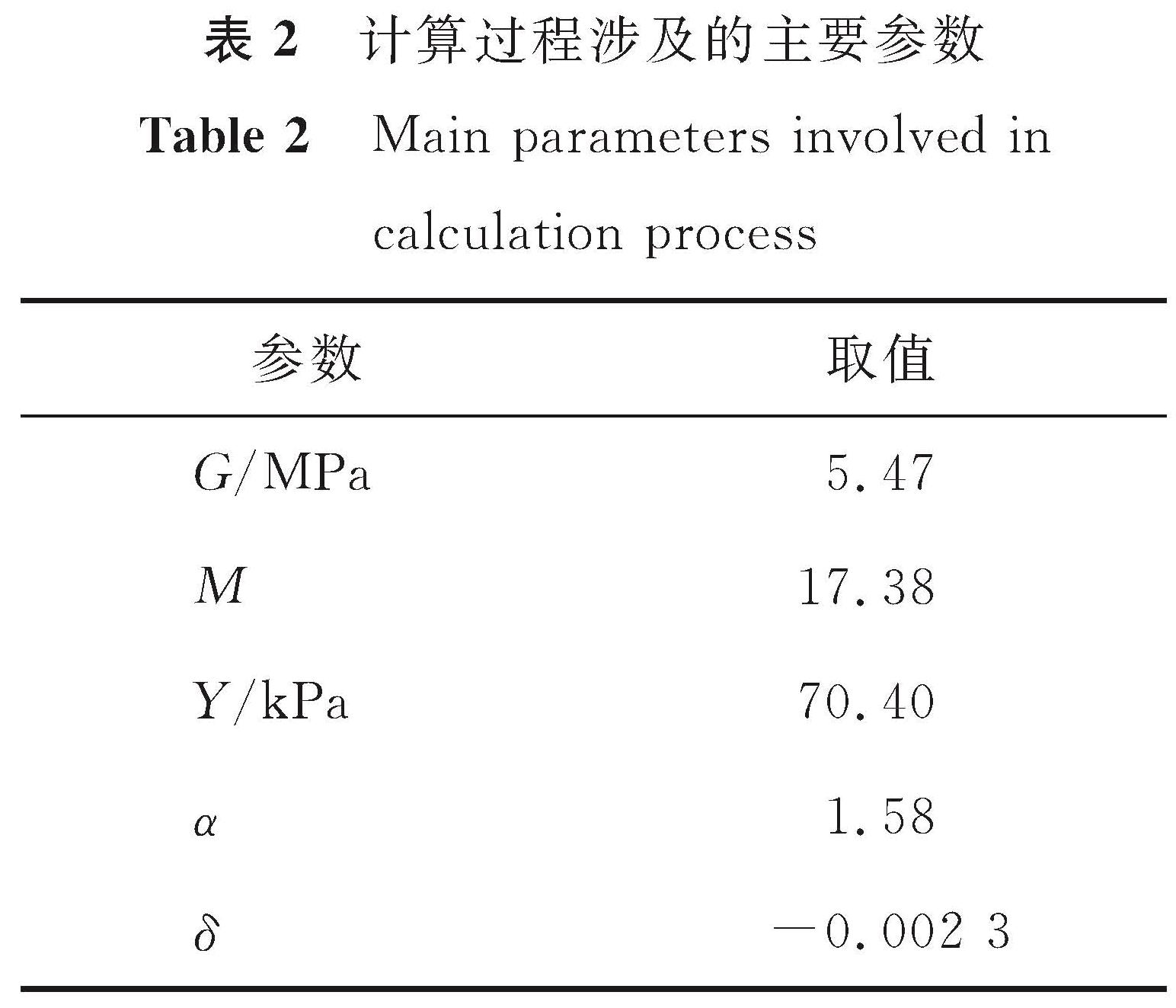
式(3)中:E为杨氏模量; G为剪切模量; Y、α、M、δ均为计算系数; v为泊松比; p₀为初始小孔压力; k为区分柱形孔(k=1)或球形孔(k=2)的参数。

当小孔压力达到p=p_1y时进入初始屈服阶段:

p_1y=2kGδ+p₀。 (4)

土体变形在开始阶段是完全弹性的,弹性应力-应变关系可表示为

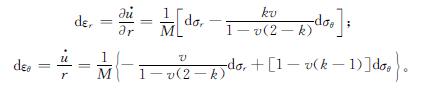
应力和位移的弹性解为

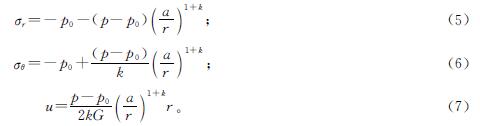
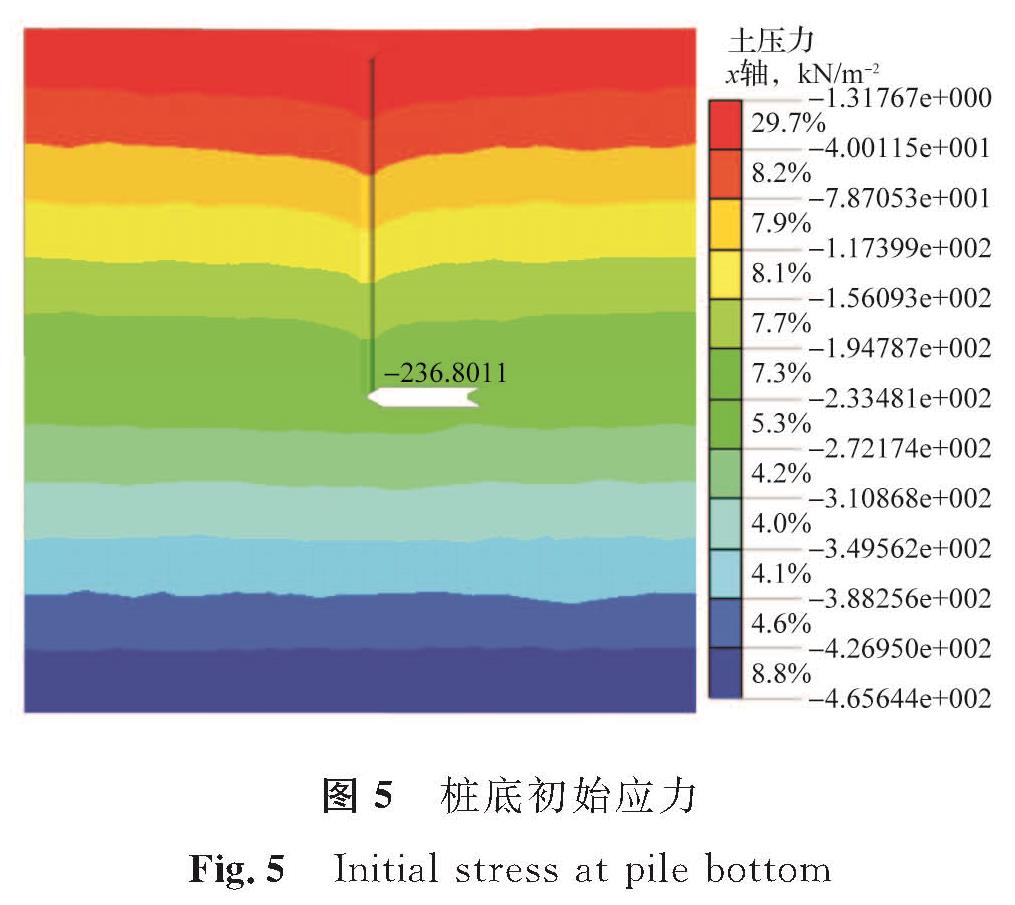
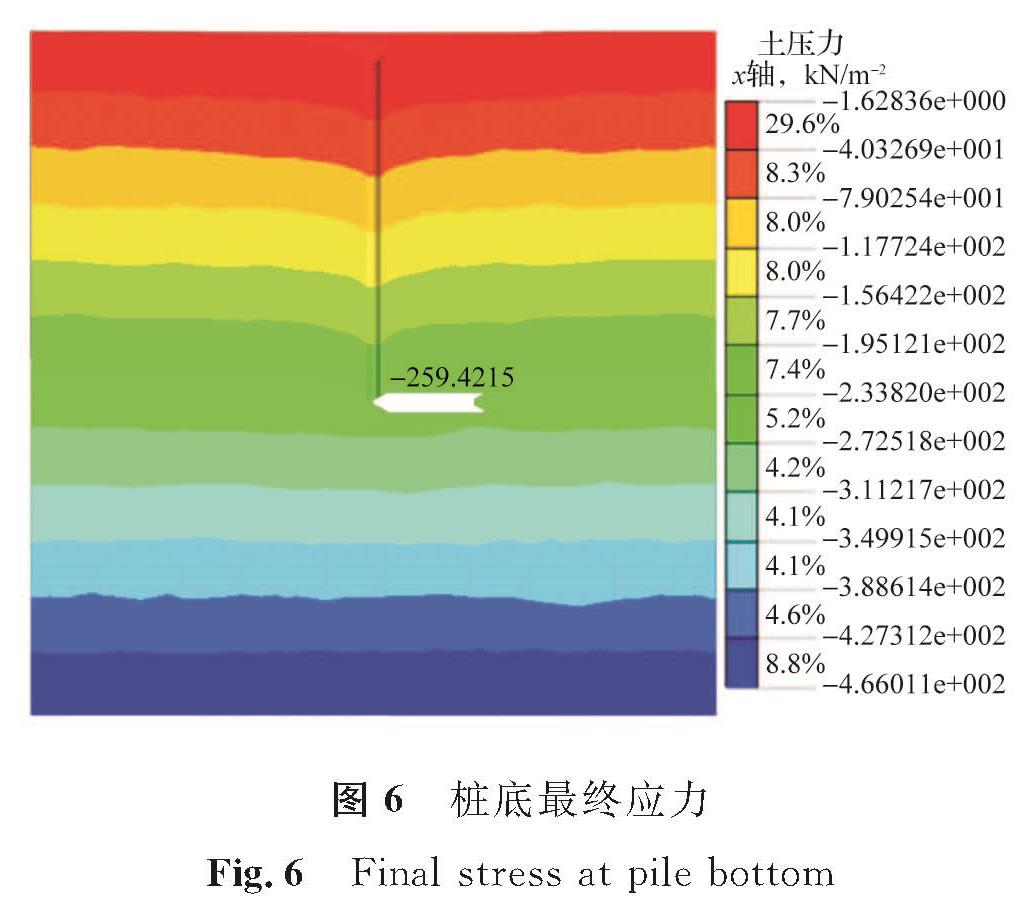
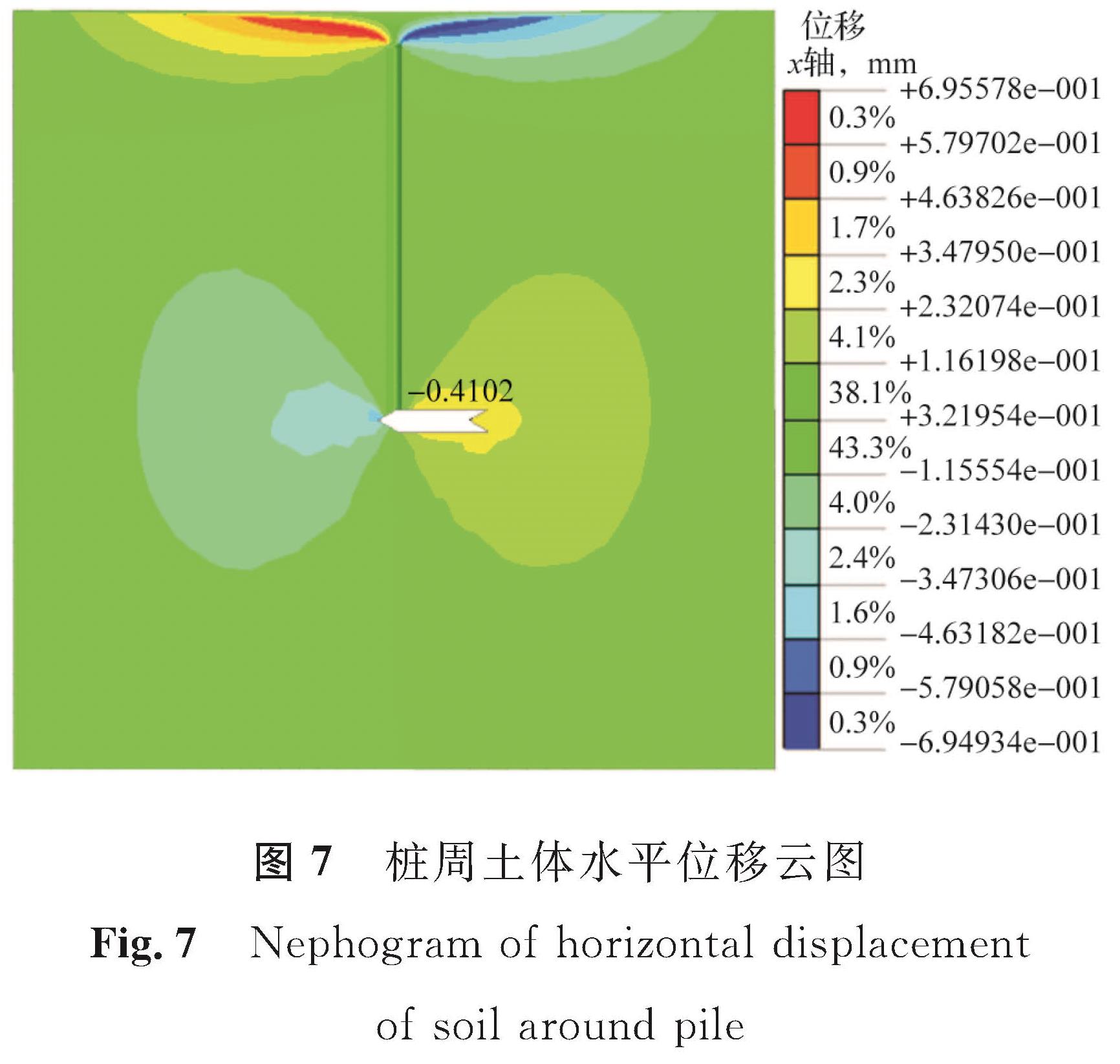
如表1所列,用于示例的黏土中桩体超灌3.0 m模型的参数E=15 MPa,v=0.37,C=28 kPa,φ=13°,k=1,桩体半径a=0.4 m。桩底初始应力和桩底最终应力如图5、图6所示,p₀=-236.8 kPa,p=-259.4 kPa。由图7桩周土体水平位移云图可确定水平位移最大处距离中心点的距离可近似取为r=0.8 m,同时可看出桩底周围的土体水平位移主要分布在以桩底为圆心的扇形区域内。计算过程涉及的主要参数见表2。

图5 桩底初始应力
Fig.5 Initial stress at pile bottom

图6 桩底最终应力
Fig.6 Final stress at pile bottom

图7 桩周土体水平位移云图
Fig.7 Nephogram of horizontal displacement of soil around pile

表2 计算过程涉及的主要参数
Table 2 Main parameters involved in calculation process

由式(4)计算得到p_1y=-262.0 kPa,而由于最终应力p=-259.4 kPa,故土体的变形尚处于完全弹性阶段,只需计算相应的弹性解即可得到桩底附近土体的应力和应变。

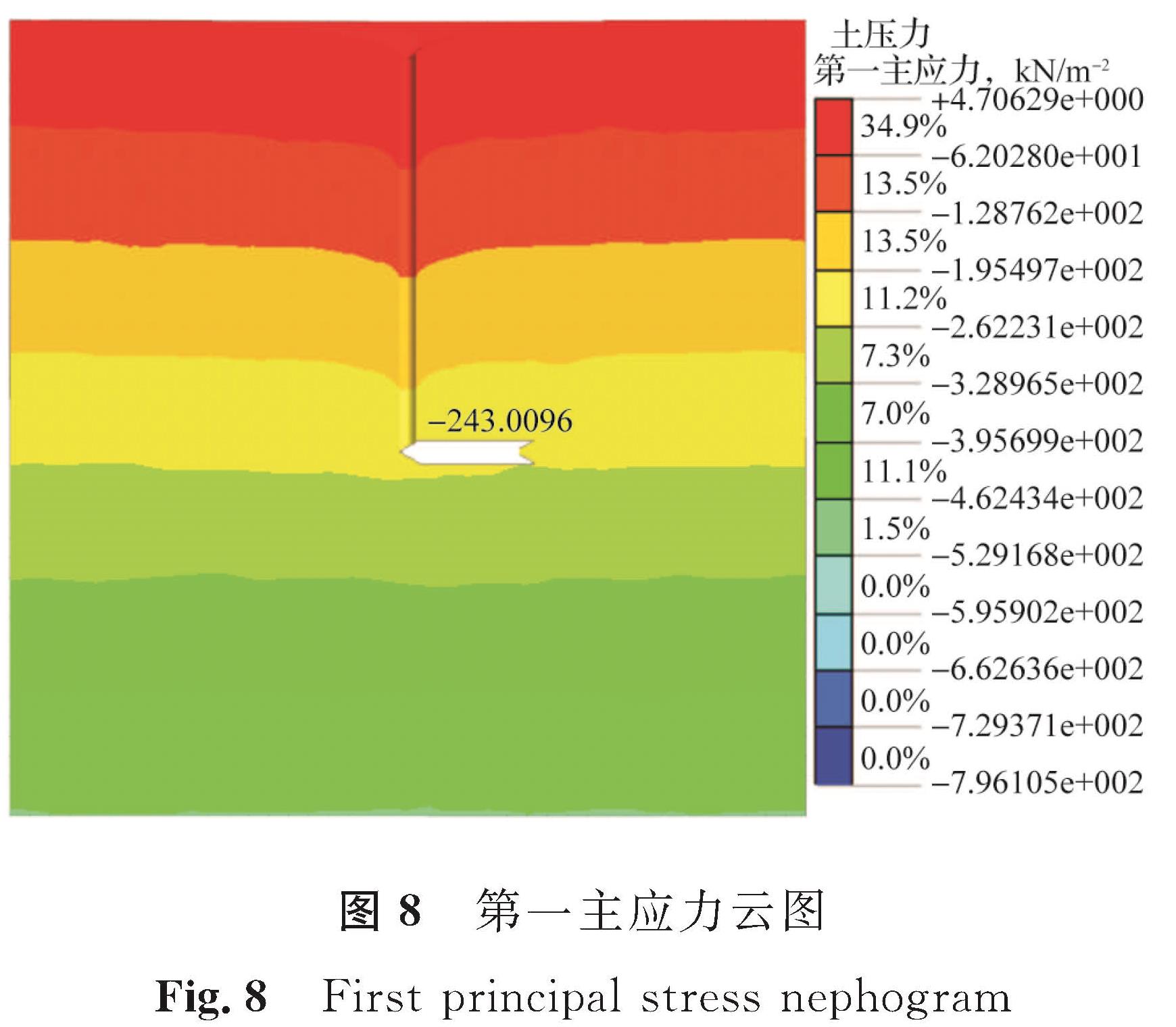
由式(5)～(7)计算得到σ_r=-242.5 kPa,σ_θ=-231.2 kPa,u=-0.413 mm。第一主应力云图和第三主应力云图如图8、图9所示,分别读取桩底部位的应力可以得到σ_r=-243.0 kPa,σ_θ=-232.8 kPa; 桩周土体水平位移云图所示的u=-0.410 mm。由此可以得出依据小孔扩张理论计算的结果与数值模拟的结果基本上相吻合,数值模拟的结果具有可信度。

图8 第一主应力云图
Fig.8 First principal stress nephogram

图9 第三主应力云图
Fig.9 Third principal stress nephogram

图 10 不同超灌高度下的桩侧土体水平位移曲线
Fig.10 Horizontal displacement curve of soil at pile side under different overfilling heights

图 10为不同超灌高度下的桩侧土体水平位移曲线。在素填土中,超灌高度从0 m增加到3 m时,桩侧土体的水平位移从20.4×10^-4(m)增加到23.9×10^-4(m); 在粉质黏土中,超灌高度从0 m增加到3 m时,桩侧土体的水平位移从6.92×10^-4(m)增加到7.16×10^-4(m); 在黏土中,超灌高度从0 m增加到3 m时,桩侧土体的水平位移从3.98×10^-4(m)增加到5.04×10^-4(m)。在3种土体中桩侧土体的水平位移均可看作随超灌高度的增加而线性增长。但由于3种土体中桩侧土体的水平位移数值均较小,同时由于在施工过程中超灌的部分将在混凝土凝固后进行凿除,所以在确保桩头质量的条件下可以认为超灌量对桩侧土体水平位移的影响不大。

通过对超灌桩桩底位移和桩侧位移的分析,我们研究了素填土、粉质黏土、黏土中单桩在超灌情况下的桩底位移和桩侧位移,揭示了在相同上部荷载的作用下,桩底位移和桩侧位移受超灌量的影响程度,得到以下结论:

1)对于桩长20 m的灌注桩,超灌高度在3 m以内时,对桩底位移的影响在允许的误差范围内。由于现场施工人员凭经验判断和水平的差异,导致超灌高度不能得到准确的控制,例如北京朝阳站工程行包通道部分,开挖后发现大量水泥粉煤灰碎石(cement fly-ash gravel,CGF)桩超灌2 m以上^[19]。虽然超灌对桩体质量没有影响,但是过大的超灌量,除产生混凝土材料的浪费之外,还会导致额外增加了土体开挖和桩头破除的工程量,同时也增加了废料运出的费用,这在很大程度上影响了工程成本的控制。

2)土体的竖向位移更多地发生在靠近桩体的部分,尤其是接近桩底的部分; 土体的水平位移更多地发生在桩底附近与水平线呈45°,半径为10 m的扇形区域; 弹性模量较小的土体中会发生更大的桩体位移。但是由于3种土体中灌注桩的桩底水平位移的数值均较小,而且在实际施工中超灌部分将在凝结后凿除,所以在确保桩头质量的前提条件下,不同的超灌量对桩体竖向位移方面的影响较小。

3)在节约成本的同时,为提高施工效率,保证施工质量,使超灌高度在大于1倍桩径的前提下尽可能地接近1倍桩径,建议使用超灌监测仪器代替传统的手动判断方法,以减少人工判断与控制造成的误差。