可转债是中国金融市场上一种十分灵活的金融衍生工具,债券持有人拥有“可以在规定时间内把所持有的债券转换为股票”的权利,可转债下有保底上不封顶的特点使其广受投资者的喜爱,因其融资成本低和股权稀释慢也越来越受上市公司的青睐。它非常依赖利率和股票等多种标的,具有很强的路径依赖性; 同时赋予参与方多种权利,如赎回权、回售权等。可转债集债权性、股权性和期权性于一身。自2017年中国证券监督管理委员会颁布再融资新规后,政策上的支持让可转债的发行数量和发行规模较之前出现了爆发式增长,成为金融市场不可分割的一部分,因此对其精准定价有重要的现实意义。
在20世纪70年代,Black等[1]开创出的布莱克-斯科尔斯(Black-Scholes,BS)模型为金融市场衍生产品的定价奠定了良好的基础。早期大多数研究者认为可转债的定价应基于公司价值定价模型,因为该类方法能够将可转债很好地与信用风险模型相结合。Ingersoll[2]基于公司价值单个因素,首次使用BS模型得到了可转债的解析解。Brennan等[3]引入随机利率模型,把定价过程转化为双因素模型,但结果表明利率随机化对价格变动的影响并不显著。基于公司价值的定价方法其结果与实际差距较大,主要原因是公司价值很难准确获得。为了克服这种结构式定价的缺点,许多研究者将可转债的定价基于公司股价,如Mcconnell等[4]提出了基于股价的单因子模型,并进一步扩展成基于股价和利率的双因子模型。随后人们通过大量实证研究发现,信用风险也是可转债定价的必要因素,其中Ayache等[5]提出的带有信用风险的模型受到了广泛的关注与运用。采用数理模型方法解决可转债定价问题其优点是放宽了定价假设条件,使定价假设不再那么严格,能获得与实际价格相符的定价,但存在计算量大的弊端。
目前针对中国可转债定价的主要方法有分解定价法[6-7]、偏微分方程定价法[8-9]、树模型法[10]、蒙特卡洛模拟法[11-12]等,如果计算的时间间隔设置得足够小,则以上定价方法皆趋于偏微分方程定价法,这些定价方法在原理上是相似的。资产定价模型的关键之一是对波动率的优化,大多研究者采用时间序列中的模型拟合,此类方法虽然能较好地刻画出波动的聚集性,但体现不出实际资产价格还存在着自相似性和增量的不平稳性。为了更好地拟合资产的实际价格,解决“微笑波动率”现象,Bojdecki等[13]首次提出了次分数布朗运动,它是修正后的分数布朗运动,不仅保持了分数布朗运动的自相似性、长记忆性和赫尔德连续性,还保持了二阶矩增量的不平稳性。Tuder[14]发现次分数布朗运动的退化速度快于分数布朗运动,分别以N2H-3和N2H-2的速度退化,更加符合资产的长记忆性; Dai[15]和Prakasa Rao等[16]分别对次分数布朗运动的极限和线性乘子的非参数估计问题进行了深入的研究。El-Nouty等[17]把次分数布朗运动和布朗运动进行线性组合,得到了混合次分数的环境。实际金融市场中,标的资产价格不仅会随机连续波动,还会因为重大事件的影响产生不连续的波动,即股价会发生“跳跃”,进而影响期权的定价,因此如何模拟标的资产价格变动的跳跃情况也是研究者一直在探索的课题[18-19]。综观已有研究鲜有涉及混合次分数布朗运动跳扩散环境下的可转债定价,故本研究综合考虑可转债标的资产的长记忆性和跳跃性的特点,提出该定价策略,以解决资产收益率不平稳的增量性,并结合国内实际可转债市场进行实证分析。
1 预备知识设次分数布朗运动{BHt,t≥0}是Hurst(赫斯特)指数为H(H∈(0,1))的连续高斯过程,其期望为零,协方差为
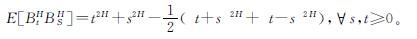
当H=1/2时,BHt为标准的布朗运动,记为Bt。
为了将次分数布朗运动推广到混合次分数布朗运动模型,假设标准布朗运动Bt与次分数布朗运动BHt相互独立,混合次分数布朗运动为
ξHt=ξHt(δ,σ)=δBt+σBHt。 (1)
式(1)中:δ、σ分别为标准布朗运动Bt和次分数布朗运动BHt的波动率。混合次分数布朗运动主要的性质包括自相似性和长相依性,表现如下:
1)对于任意常数a>0,有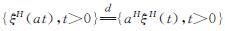 ;
;
2)当H>1/2时,若相关性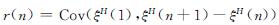 ,那么
,那么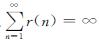 。
。
混合次分数布朗运动的协方差为
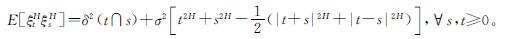
从广义上看,可转债本身就有普通债券的属性,又由于转股条款的存在,进一步增加了可转债的价值,可以看作内嵌了一个美式看涨期权; 但在有效市场假设下,美式看涨期权对应的标的股票在期限内没有进行分红,就可以把它当成欧式看涨期权。此外,当股价触发到赎回价格并满足赎回条件时,有部分为了投资者转股而发行可转债的上市公司不会提前赎回可转债,因为他们会为了自身财务状况选择不再支付债券后续的利息和本金; 但对业绩优良的上市公司而言,为了不稀释自身股权,则会选择在合适的时间进行转股。当股价触发回售价格并满足回售条件时,理性投资者大多会将可转债按规定价格回售给上市公司; 考虑到可转债的低利息、可转股,还能向下修正转股价格,可转债续存期间违约的概率非常小,可将违约风险忽略不计,所以本研究只考虑可转债的赎回条款和回售条款。则有
V=B+C+R。 (2)
式(2)中:B为债券部分价值; C为欧式期权价格; R为条款的期权价格。
2 定价模型假设混合次分数布朗运动跳扩散环境下可转债的标的股票价格满足如下的随机微分方程:
dSt=μStdt+δStdBt+σStdBHt+γStdNt。 (3)
式(3)中:μ为该股票价格的平均收益率; γ为股票价格跳跃幅度; Nt为相对应的泊松补偿过程,Nt=Qt-λt,Qt是强度为λ的泊松过程,且Nt、Bt与BHt两两独立。
2.1 数理推导2.1.1 债券部分价值债券部分价值B可以通过可转债有效期内每期的现金流贴现之和得到,即各期的应付利息和最后一期的应付债券贴现到当前时点的价值之和,具体公式如下:

式(4)中:Id为可转换债券每年应支付的利息; M为可转债的本金; d为可转债剩余持有年限; r为市场无风险利率; n为可转债发行总年限。
2.1.2 混合次分数布朗运动跳扩散条件下的期权价值假设:市场不存在交易成本与税收,市场不存在可供套利的交易策略,可转债的发行和转股对股价的影响可以忽略,公司不发放股利和利息,期权部分价值作为欧式期权进行计算,可转债的转换发生时间为债券到期时刻T。
定理1 假设标的资产满足式(3),那么可转债期权部分C满足如下偏微分方程:

证明:利用Δ-对冲原理构建一个投资组合,在无套利条件下,该组合由一份期权和Δ份原生资产构成,则在t时刻该投资组合的价值为Πt=C-ΔSt; 且在(t,t+dt)时段内,该投资组合的变化为dΠt=dC-ΔdSt。
由伊藤公式及式(3)得
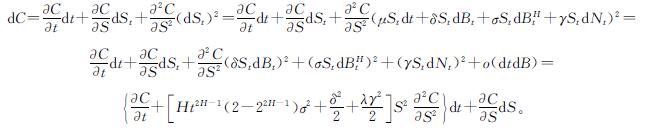
因此得
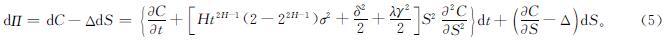
由Δ-对冲原理可知,投资组合Π是无风险的,式(5)中取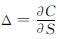 ,且有如下方程成立:
,且有如下方程成立:
dΠt=rΠdt=r(C-ΔSt)dt。(6)
联立式(5)和式(6),化简后得
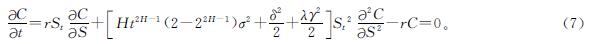
在到期日t=T时刻,有C(T,ST)=max(ST-K,0),从而定理1得证。
定理2 假设标的资产价格满足式(3),固定敲定价格为K,到期日为T的欧式看涨期权在t∈[0,T]时间的价值C(t,St)为
C(t,St)=StN(d1)-Ke-r(T-t)N(d2)。 (8)
式(8)中:
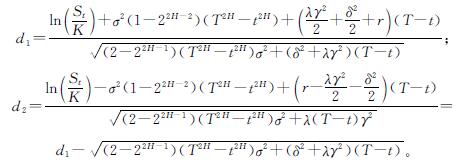
证明:由定理1可知,式(7)中期权C(t,St)为满足一维抛物方程的Cauchy问题,因此可以寻找合适的变量进行代换,转化为热方程Cauchy问题,从而快速求解。采用如下变量替换:
x=lnSt,τ=T-t,W(τ,x)=C(t,St)。
经偏导计算和变量代换,由式(7)可得
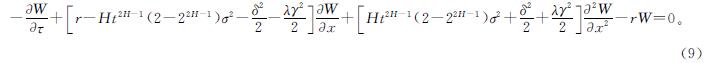
为求式(9)的解,再通过如下变量代换化简方程:
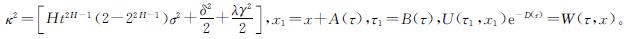
其中A(τ)、B(τ)、D(τ)为待定函数。
通过计算得到:
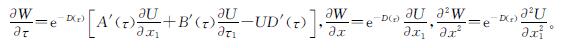
代入式(9)化简之后得
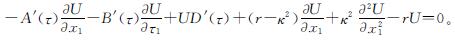
假设
A'(τ)=r-κ2,B'(τ)=κ2,D'(τ)=r。
由边界条件A'(T)=B'(T)=D'(T)=0可知:

从而有如下结果:

在到期日t=T时,期权收益为U(x1,0)=max(ex1-K,0)。
接下来把条件偏微分方程转化为常微分方程定解问题[20],得到:
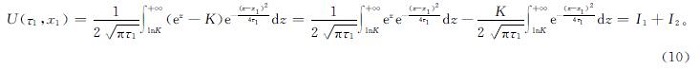
对于I1,令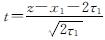 ,有
,有

对于I2,令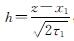 ,有
,有

所以式(10)可简化为
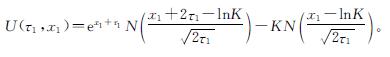
那么
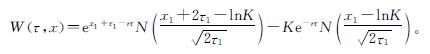
也即
W(τ,x)=exN(w1)-Ke-rτN(w2)。 (11)
式(11)中:
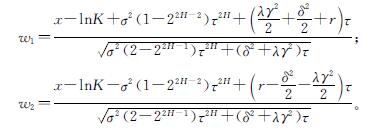
再把x=lnSt,τ=T-t,W(τ,x)=C(t,St)代入式(11),求出C的解析解即定理2。定理2得证。
在式(8)中,当H=1/2、δ=0时,式(8)变为标准布朗运动跳扩散环境下的欧式期权定价公式; 当δ=0、λ=0时,式(8)为次分数布朗运动环境下欧式期权定价公式; 当H=1/2、δ=0、λ=0时,式(8)为经典BS公式。
2.1.3 可转债条款期权价值模型回售条款规定当该公司股价连续一段时间小于转股价某一比例时,可以给投资者一种权利,让投资者以发行公告中规定的回售价格卖出手里持有的可转债,从而保护投资者的利益,因此回售条款可以看作债券持有人拥有的一项看跌期权,令可转债回售条款的执行价格为Xback,可求得回售条款的期权价格Rback,其中Xback一般为0.7K,回售条款期权价格与2.1.2节中式(8)的计算方法相同,回售条款的价格为
Rback(t,St)=-StN(-d3)+Xbacke-r(T-t)N(-d4)。 (12)
式(12)中:

赎回条款规定当该公司股价连续一段时间大于转股价某一比例时,可以给发行公司一种权利,让它以发行公告中规定的赎回价格赎回还在流通的所有可转债,对发行方而言不用稀释股权也无须再还本付息,从而保护发行方的利益,对投资者而言此时行权也可获得较高收益,因此是最优的操作策略。赎回条款是一项对发行方而言的看涨期权。令可转债赎回条款的执行价格为Xredeem,可求得赎回条款的期权价格Rredeem,其中Xredeem一般为1.3K,计算公式为
Rredeem(t,St)=StN(d5)-Xredeeme-r(T-t)N(d6)。 (13)
式(13)中:
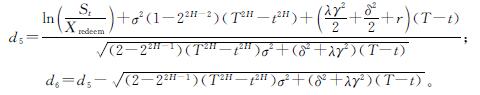
假设某上市公司在t=0时发行了可转换公司债券。用(St)t≥0表示该上市公司的股票价格,用(Vt)t≥0表示该可转债的价格,那么可转债价格的组成为
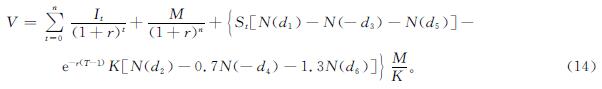
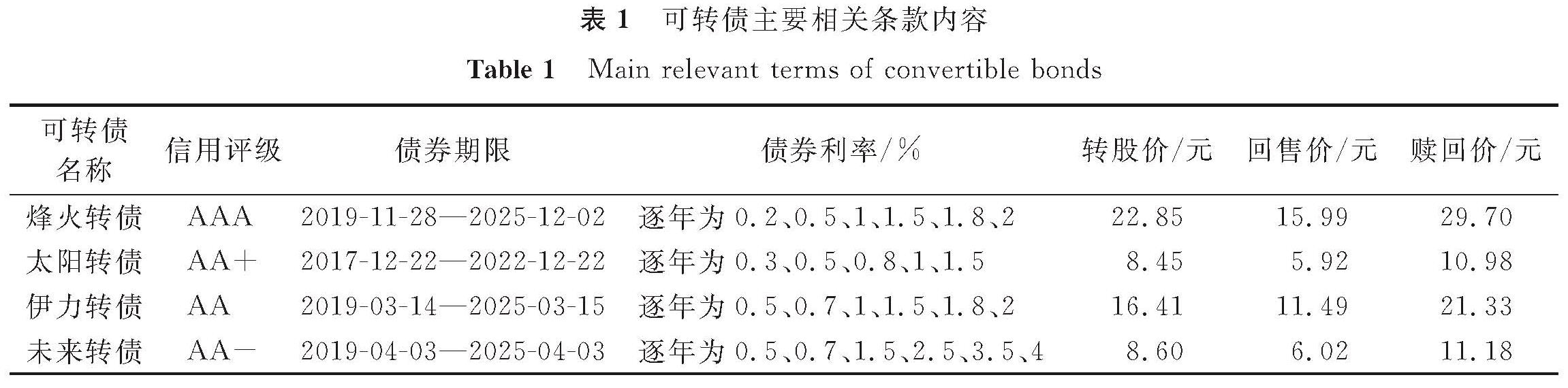
可转债数据来源于同花顺、万德资讯和可转换公司债券上市公告书,包含了目前发行流通的300多只可转债,根据可转债发行条款是否规范完整、融资规模和发行数量、可转债及其标的股票在样本区间有无停牌情况、市场价格数据是否充足、财务情况、信用评级、债券期限等特征,以烽火转债、太阳转债、伊力转债、未来转债为例进行实证分析,可转债主要相关条款内容见表1。
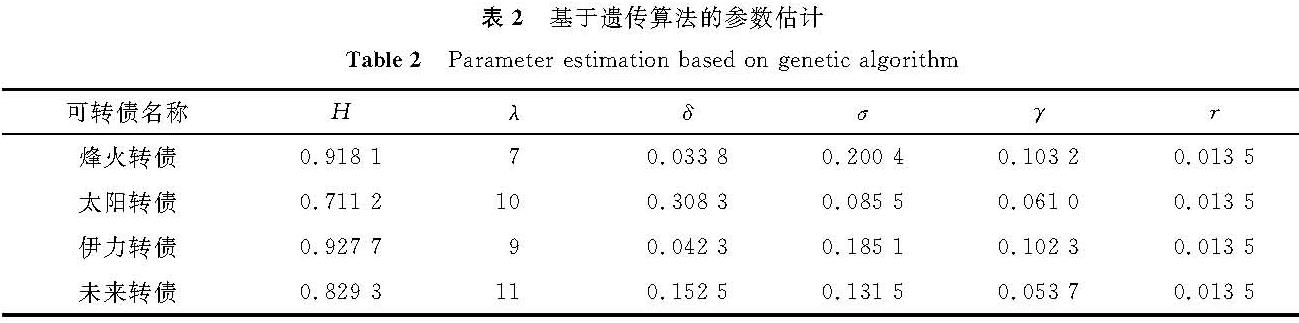
3.2 参数估计3.2.1 基于遗传算法的参数估计
本研究采用混合次分数布朗运动跳扩散环境刻画可转债价格变化的行为模式,而如何有效地估计方程参数将是本定价模型应用于实践的重要环节。传统的极大似然法和模拟退火算法在实际应用中都容易陷入局部极值而丢失最优解,且计算时间较长。本研究采用具有并行搜索和不失最优解的遗传算法来寻找模型中的参数,该算法的原理是先随机产生一系列初始解,然后构造解的适应值,在每一次迭代中用适应值来测量问题解的优劣,淘汰不满足条件的解,通过选择、交叉和变异运算形成下一轮迭代的解集,经过一定次数的迭代后,算法会收敛于全局最优解。本研究设计的遗传算法主要步骤有编码、适应度函数、选择、交叉与变异。
1)编码。为了简化编码和译码环节,本研究染色体采用实值编码。例如,有一个四维向量[a,b,c,d],其中每个维度代表一个参数,不同的四维向量代表不同编码串,每个编码串就是一组理想参数。以[x1=0.85,x2=3,x3=0.32,x4=0.06,x5=0.3]为例,表示本文模型中各个参数值为H=0.85,λ=3,σ=0.32,γ=0.06,δ=0.3。这样就得到了一组待估参数的取值,不同的向量就表示不同的待估参数组。
2)适应度函数。第k个个体的适应度函数为

式(15)中:n为样本容量; Fk为种群中第k个个体所代表的模型定价效果的优劣程度,模型定价效果与函数值成反比。
3)选择。采用随机遍历抽样,依照个体的适应度值计算每个个体在子代中出现的概率,并按照此概率随机选择个体构成子代种群。
4)交叉与变异。本研究采用双亲双子法产生一个随机位,交换该随机位之后的所有基因,产生2个新的子代; 变异方式则采用实值种群变异。
本研究采用每只可转债在上市首日到2021年6月30日的数据为样本,进行遗传算法估计。以太阳转债为例,根据样本数据、染色体长度和种群规模的大小,设遗传算法的进化数为300、交叉概率为0.5、变异概率为0.07、初始种群规模为20。得到待估参数为:[H,λ,δ,σ,γ]=[0.71,10,0.31,0.09,0.06],此时适应度函数的值即均方误差为0.001。个体和种群收敛情况如图1所示。
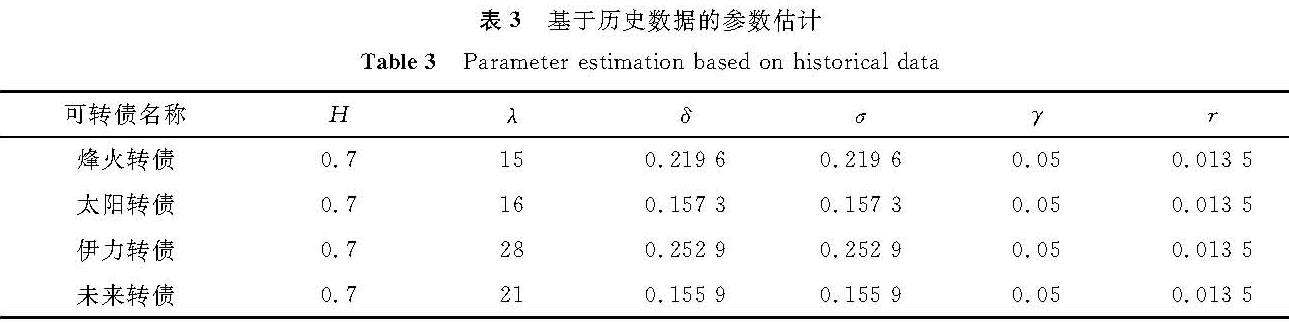
3.2.2 基于历史数据的参数估计本研究基于历史数据的波动率采用标准差公式来定义:

式(16)中:ri=lnSi-lnSi-1; μ=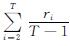 。
。
本文模型中由于考虑了股票价格的跳跃因素,计算波动率时就无须考虑跳跃的影响。定义发生跳跃的情形为当日涨跌幅超过5%,剔除这些日期的数据,得到模型的历史平均波动率。以太阳转债为例,从2018年1月16日到2021年7月16日,共有850个数据,其间振幅超过5%的日期有55 d,将剩下的795个数据进行计算,其中第i日股票价格的连续复利收益率为ri,标准差σ1为对应的日化历史波动率,那么年化波动率为σ=σ1×y1/2,y为年交易天数,计算得到太阳转债的波动率为15.73%。
经典BS模型中的波动率采取所有样本价格计算,得到波动率的估计值为30.86%。
由于难以区分混合次分数布朗运动和标准布朗运动各自占的比例,令参数δ等于σ; 参数λ选取标的股票波动幅度大于5%的年均次数,次数为16; Hurst指数取常规的0.7; 纯债贴现率取2020年中国人民银行的5年期国债基准利率(r=5.32%); 无风险利率则采用一年期定期存款利率1.35%。基于遗传算法和历史数据的参数估计分别见表2和表3。
3.3 计算结果分析
本研究利用Python软件编写对应的遗传算法程序,经计算得到混合次分数布朗运动跳扩散环境下可转债定价模型的待估计参数值,然后利用该参数值对上市首日可转债价格进行模拟定价。为了更加直观地展示定价结果,本研究以太阳转债为例对算法进行了3年的跟踪测试。
3.3.1 债券部分价值计算由式(4)可求出可转换的纯债部分价值,为方便计算忽略了发行日期到上市日期的时间间隔,以太阳转债为例,面值为100元,存续期限为5年,票面利率第一年为0.3%、第二年为0.5%、第三年为0.8%、第四年为1%、第五年为1.5%,通过折现得到太阳转债的纯债券部分价值为

然后依次求得烽火转债、伊力转债、未来转债债券部分价值,分别为78.841 7、79.306 9、83.234 9元。
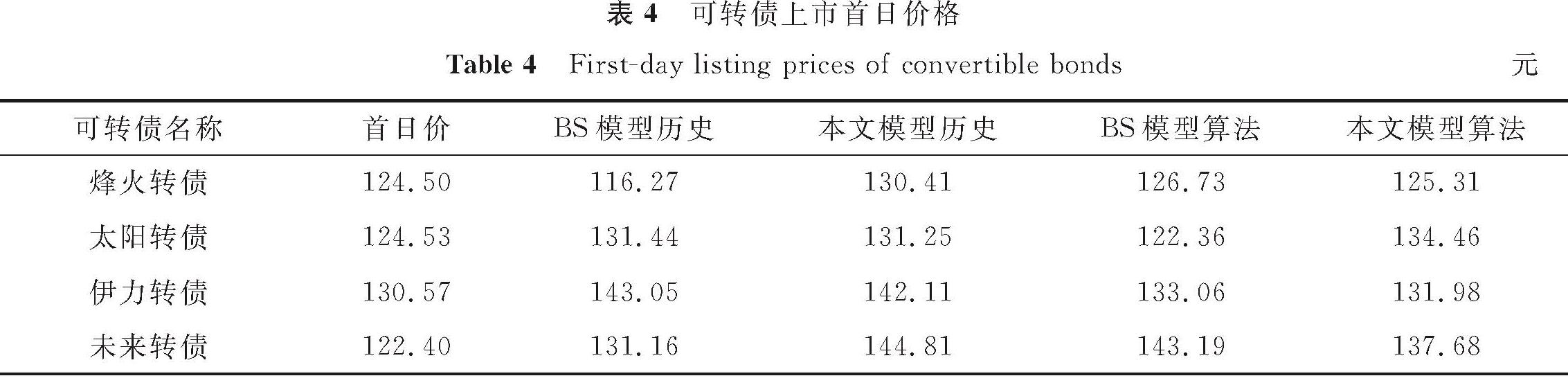
3.3.2 可转债价值计算为了说明模型的有效性,将所得结论应用到实际中去,运用式(14),通过上文得出的参数计算各模型可转债上市首日价格(表4)。
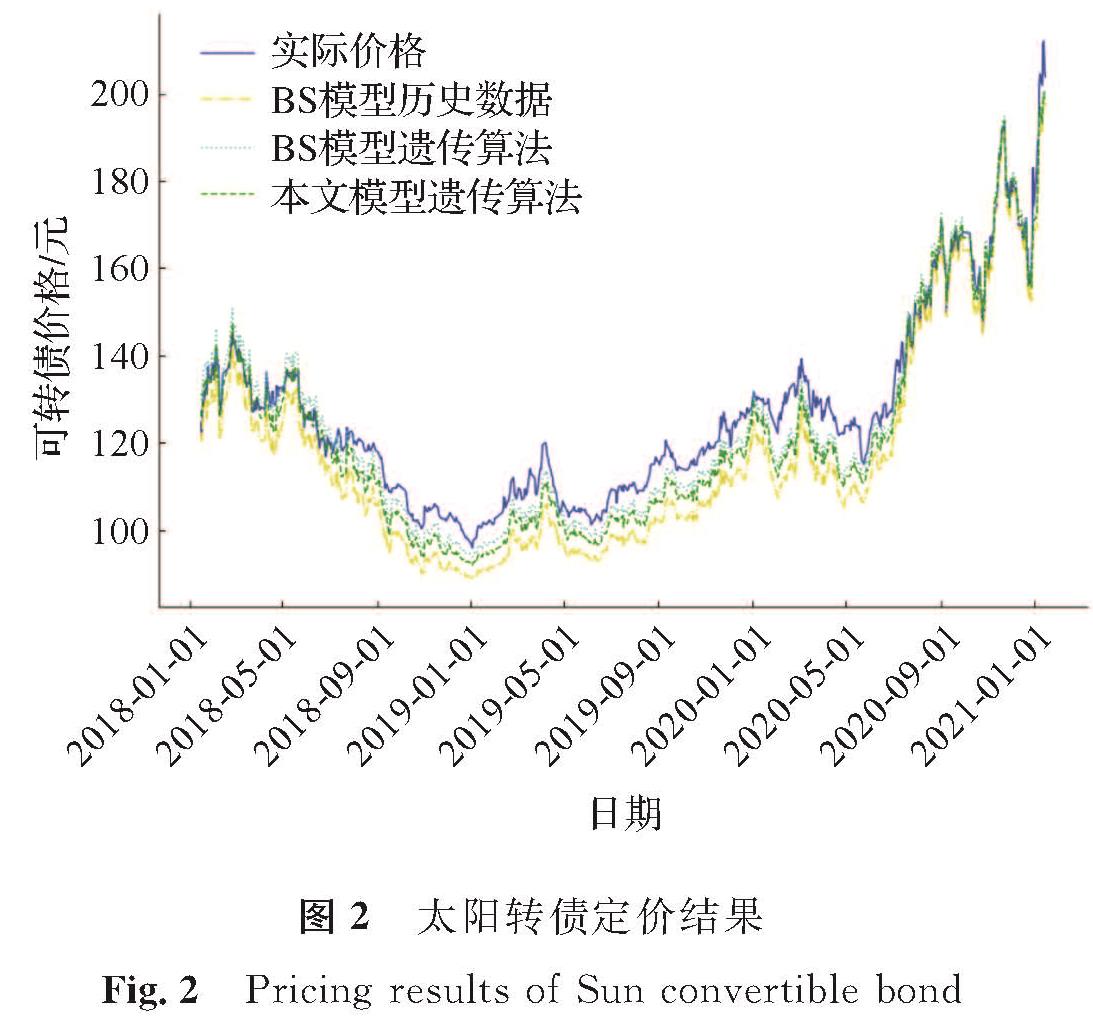
以太阳转债为例,将其上市开始后3年内每个交易日的理论价值与实际价格做比较,得出太阳转债定价结果(图2)。
对图2进行直观分析可知,用遗传算法估计的参数效果明显优于历史数据估计的参数; 模型价格在上市开始前半年对实际价格的拟合效果略弱于半年之后,其原因在于可转债还未到达转股日期,即使出现较低的溢价率也不能将可转债转为正股进行套利,所以实际价格会与理性定价产生较大的差距,并且在下跌趋势中,低的溢价率预示着正股价格还会下降,当溢价率趋于零时,也意味着反转即将到来; 在后半段上升区间中,理论价格与实际价格拟合得非常好,由于此时投资者可以随时转股,溢价也不会太大,理论模型也就更加有效地反映出实际价格。可见,本文模型相对于传统BS模型更加平滑,从而与实际价格更贴切,因此混合次分数布朗运动跳扩散模型是有效的。
接下来通过引入反映理论价格和实际价格偏离程度的均方误差(MSE)来定量比较各个模型的优劣程度,各转债上市首日至2021-06-30日理论价值与实际价值的均方误差见表5。
表5 各转债上市首日至2021-06-30日理论价值与实际价值的均方误差
Table 5 Mean square error of theoretical and actual value from listing date to 2021-06-30 of each convertible bond
从表5中可以看出,本文模型的均方误差明显小于传统BS模型,4个转债的均方误差平均减少0.34%; 用遗传算法估计得到的参数定价效果也同样显著优于用历史数据估计的参数,BS模型和本文模型均方误差各减少0.44%和0.17%,平均减少约0.31%,进一步验证了图2的结果。
4 结 语目前可转债在中国还属于新兴金融衍生产品,建立混合次分数布朗运动跳扩散环境下可转债的定价模型与公式,无论在理论上还是实务上都有着重要的意义。本研究将可转债分解的结构化思路与上海证券交易所对可转债的定义类似,即把可转债分解为债券和期权价值之和; 又由于股价波动拥有自相关、非平稳增量和跳跃的特点,本研究选择在混合次分数布朗运动跳扩散环境下推导出可转债期权部分的价格,且将条款的影响考虑在可转债定价内,最终确定可转债定价公式,并实证对比传统的BS模型,得出本文模型定价更为合理。
- [1] BLACK F, SCHOLES M S. The pricing of options and corporate liabilities[J].Journal of Political Economy,1973,81(3):637.
- [2] INGERSOLL J E. A contingent-claims valuation of convertible securities[J].Journal of Financial Economy,1977,4(77):289.
- [3] BRENNAN M J, SCHWARTZ E S. Analyzing convertible bonds[J].Journal of Financial and Quantitative Analysis,1980,15(4):907.
- [4] MCCONNELL J J, SCHWARTZ E S. LYON taming[J].Journal of Finance,1986,41(3):561.
- [5] AYACHE E, FORSYTH P A, VETZAL K R. The valuation of convertible bond with credit risk[R].Waterloo: University of Waterloo,2003.
- [6] FENG Y, HUANG B, HUANG Y. Valuing resettable convertible bonds: based on path decomposing[J].Finance Research Letters,2016,19:279.
- [7] 张茂祥.基于DEA方法的可转债投资绩效研究[J].改革与开放,2021(7):11.
- [8] 常竞文,王永茂.随机利率模型下基于Tsallis熵分布的可转债定价[J].运筹与管理,2020,29(7):189.
- [9] 陈飞跃,陈煜,杨蓉,等.混合分数布朗运动下分离交易可转债的定价[J].经济数学,2020,37(3):133.
- [10] 范宇珩,张胜良.基于二叉树模型的物流业可转债价值分析:以长久转债(113519)为例[J].物流工程与管理,2020,42(10):1.
- [11] 易永坚,张毅.基于“徐工转债”的可转债发行定价问题研究[J].金融管理研究,2020(1):195.
- [12] 朱妮洁.基于Monte-Carlo模拟的可转债定价模型[J].经济研究导刊,2018(10):94.
- [13] BOJDECKI T, GOROSTIZA LG, TALARCZYK A. Fractional Brownian density process and its self intersection local time of order[J].Journal of Theoretical Probability,2004,17(3):717.
- [14] TUDER C. Some properties of the subfractional Brownian motion[J].Stochastics,2007,79(5):431.
- [15] DAI H S. Random walks and subfractional Brownian motion[J].Communications in Statistics Theory and Methods,2016,45(10):2834.
- [16] PRAKASA RAO B L S. Nonparametric estimation of linear multiplier for processes driven by subfractional Brownian motion[J].Stochastic Analysis and Applications,2019,37(5):799.
- [17] EL-NOUTY C, ZILI M. On the sub-mixed fractional Brownian motion[J].Applied Mathematics: A Journal of Chinese Universities(Series B),2015,30(1):27.
- [18] 杨月,王永茂.带跳次分数布朗运动下亚式期权定价[J].数学的实践与认识,2020,50(13):131.
- [19] 徐峰,周圣武.次分数跳:扩散过程下交换期权的定价[J].数学的实践与认识,2018,48(24):299.
- [20] 霍海峰,温鲜,邓国和.分数次布朗运动的欧式障碍期权定价[J].经济数学,2009,26(4):97.
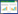 图 1 个体和种群收敛情况
Fig.1 Convergence of individuals and populations
图 1 个体和种群收敛情况
Fig.1 Convergence of individuals and populations