股票价格预测是金融领域重要且具挑战性的问题之一,故吸引了很多研究者。研究结果表明,股票市场是可预测的,合理准确的股价预测能产生较高的财务收益,并可对冲市场风险[1-3]。但股价走势受众多因素的共同影响,呈现出非线性、非平稳性、低信噪比与长记忆性等特点,是一个极为复杂的动力学系统[4]。正因如此,一般方法很难挖掘到股票价格中的有效特征进行预测。
1970年Fama提出有效市场假说[5-6],该理论认为股价波动服从随机游走而不具有可预测性。但在之后的研究中对市场有效性程度争论不断,Shleifer等[7]认为金融市场并不总是具备市场有效性的。实际上,信息经济学研究者认为市场要想实现真正的有效性,就必须具有必然的无效性[8]。随着关于金融市场的研究逐步深入,Jegadeesh等[9]发现,相比短期市场,股票市场会存在中期惯性和长期反转,从而可预测性更高。2004年Lo提出适应性市场假说[10],该理论认为市场环境不断变化,投资者要求的风险溢价时变性造就了金融市场的可预测性,而市场具有可预测性是维持其有效性必不可少的动力。
解决股票价格预测问题的模型可归结为两类。由于股票价格是一种时间序列,其传统预测方法是利用计量经济学模型根据获取到的历史数据对未来值进行预测,因此第一类划分为计量经济学模型。常用方法有自回归模型(autoregressive model,AR)、移动平均模型(moving average model,MA)、自回归移动平均模型(autoregressive moving average model,ARMA)和差分移动平均自回归模型(autoregressive integrated moving average model,ARIMA)[11],如Devi等[12]利用差分移动平均自回归模型对中型股进行趋势预测。第二类是基于软计算的模型。由于金融时间序列存在高维度、非线性等特点,这些基于软计算的模型从过去的支持向量机(support vector machine,SVM)[13]与随机森林(random forest,RF)[14]等传统机器学习模型逐渐演化为卷积神经网络与循环神经网络等深度学习模型。深度学习从2006年开始逐渐成为人工智能领域热门技术之一,在语音识别[15]、计算机视觉[16]与自然语言处理[17]领域取得了巨大的成功。近年来,研究者探索深度学习在金融领域的应用,已经取得了初步成果:如Fischer等[18]成功运用LSTM(long short-term memory,长短期记忆网络)方法预测了指数时间序列。杨青等[19]的研究发现深度学习在预测精度与预测结果稳定性方面优于SVM、MLP(multilayer perceptron,多层感知机)及ARIMA; 乔若羽[20]的研究结果表明LSTM和GRU(gate recurrent unit,门控循环单元)的预测精度高于卷积神经网络(convolutional neural networks,CNN)等多种深度学习方法。
2014年Goodfellow等[21]提出了生成式对抗网络模型(generative adversarial network,GAN),它通过生成器和判别器互相博弈学习生成更精确的数据,以实现纳什均衡为最终优化目的。最近几年GAN广泛应用于复杂分布上,一经提出就迅速成为深度学习领域新的研究热点,同时其相关理论研究与实践应用也在迅速扩展。目前,GAN已经成功地应用于图像修复、语义分割和视频预测[22]等领域,Zhang等[23]发现GAN在真实数据上的收盘价预测方面优于LSTM。
综合上述文献可知,深度学习因对复杂非线性序列具备强大的拟合能力而在股价预测方面体现出了一定的优势。但当前对深度学习在金融市场的应用研究还存在一些不足:一是多数研究是预测股价数值而非涨跌方向,这样的预测结果并不具备实用性; 二是当前很多研究只是使用一种时间尺度下的数据进行预测,不能充分提取研究对象的有效信息。为解决上述问题,本研究提出一种基于目前深度学习领域中热点模型GAN的变体模型GAN_BiLSTM(generative adversarial network based on bidirectional long-short-term memory network,基于双向长短期记忆网络的生成式对抗网络)对沪深300指数收盘价格进行预测,并使用大众熟悉且历史股价稳定的建设银行与陕西煤业股票数据进行模型有效性验证。
1 方法与模型
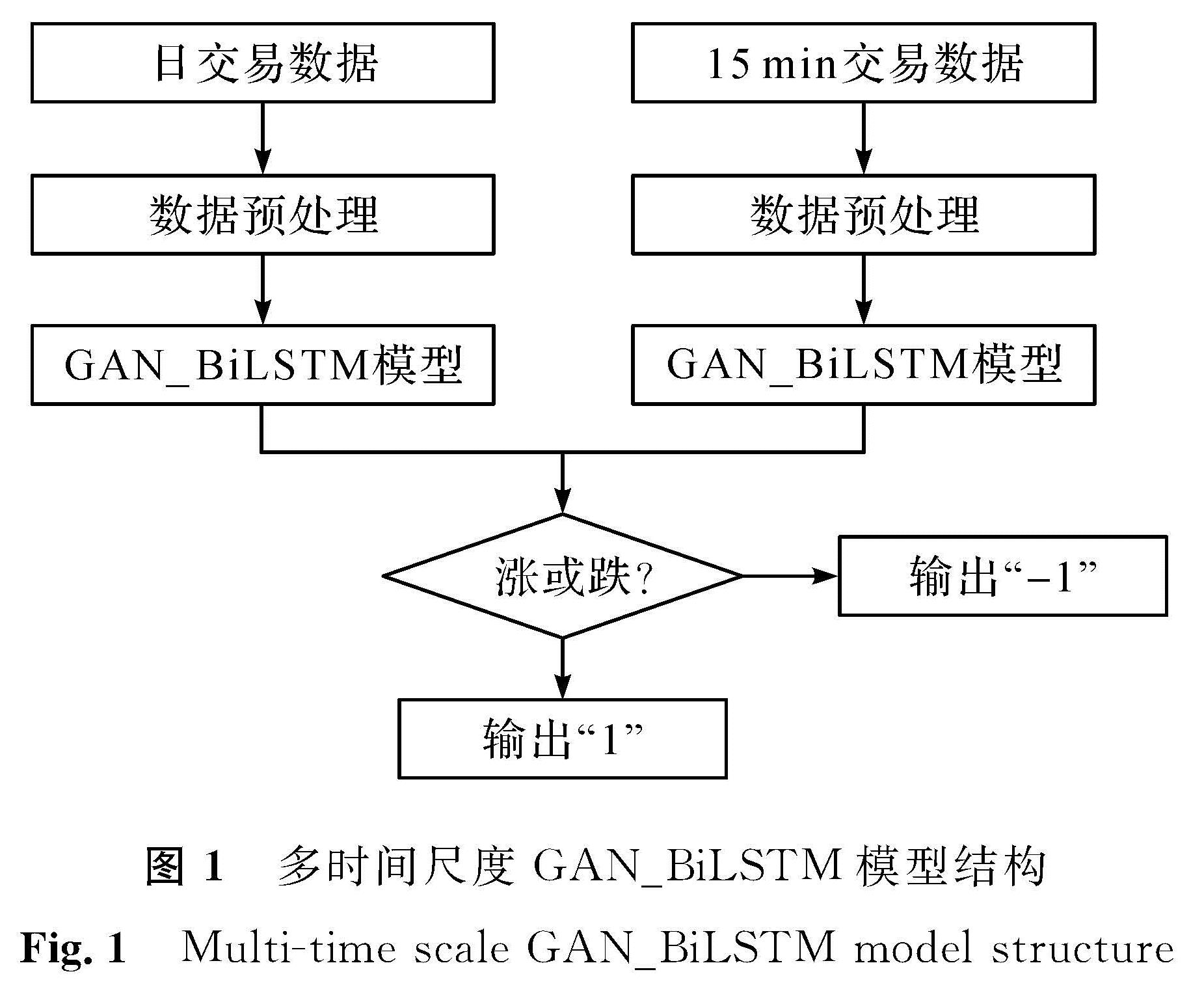
本研究提出利用对抗训练模拟经验丰富的股票交易员使用指标数据预测股价,然后用历史数据判断预测是否准确,并充分利用不同时间尺度数据来同时提取长期(日交易数据)与短期(15 min交易数据)信息,以实现更优的预测效果。多时间尺度GAN_BiLSTM模型结构如图1所示,图中,“1”表示下一交易日股价将会上涨,“-1”表示下一交易日股价将会下跌。我们分别将不同时间尺度数据进行预处理,然后输入GAN_BiLSTM模型中,再将两个时间尺度下得到的数据输入判别模型中进行处理,得到最终预测结果。
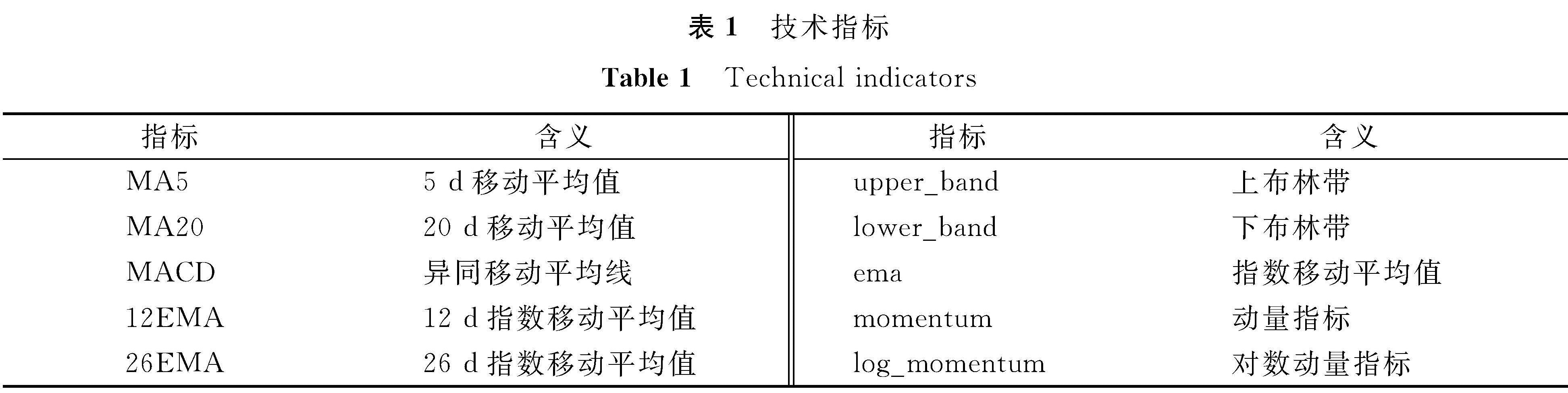
1.1 数据准备原始数据输入主要包括两个部分:股票日交易数据和15 min交易数据。在进行数据预处理之前,首先通过原始数据生成对应时间尺度的相关技术指标数据(技术指标见表1)、傅里叶变换提取到的股票整体与局部趋势数据及基于ARIMA降噪后的预测价格,以便尽可能多地挖掘该股票的有效信息。然后对数据质量进行统计检查,以确保数据不受异方差、多重共线性和序列相关性的影响。最后利用一种基于梯度提升树回归的算法XGBoost(extreme gradient boosting,极端梯度提升模型)进行特征重要性分析与筛选,从而获得对目标股票具有解释力的特征。
获取的股票数据可能存在缺值与乱序错误,因此为了取得合格数据需进行排序与插值[24]等处理。分析中使用的输入数据包括原始数据的开盘价、收盘价、最高价、最低价、交易量、数据准备阶段获取的技术指标与基于ARIMA降噪后的预测价格,共17项。为了消除各输入数据数值大小与计量单位不同的影响进而使得数据具有可比性,需进行标准化处理,计算公式如下:

式(1)中:x ~为标准化时间序列数据; xmin与xmax分别为输入时间序列数据的最小值与最大值。将标准化后的数据以8:2划分为训练集与测试集:训练集用于训练模型与调整参数,测试集用于对模型进行测试评估。
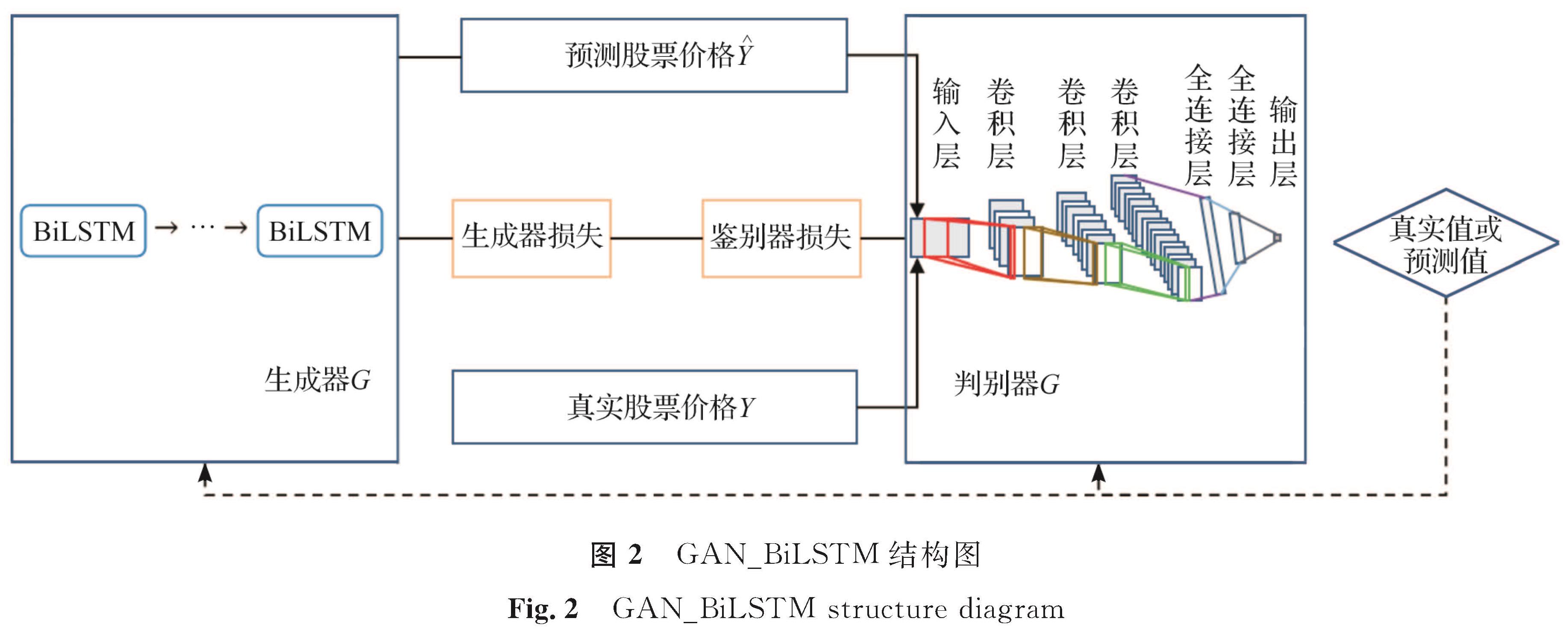
1.2 生成式对抗网络GAN可以模拟金融交易员操作,其核心思想是博弈论中的纳什均衡,模型通过GAN框架中生成器和判别器进行联合对抗训练[25]。生成器的目的是利用真实数据生成样本数据,而判别器则是用来识别输入其中的数据是真实数据还是生成的样本数据。经过一系列迭代优化,当判别器无法准确判断出数据来源时,生成器与判别器达到纳什平衡,对抗训练结束。这样我们就得到一个生成器G,这个模型可以生成我们所需要的数据。GAN_BiLSTM模型参考GAN的原理来修改其网络结构,如图2所示。
1.2.1 生成器
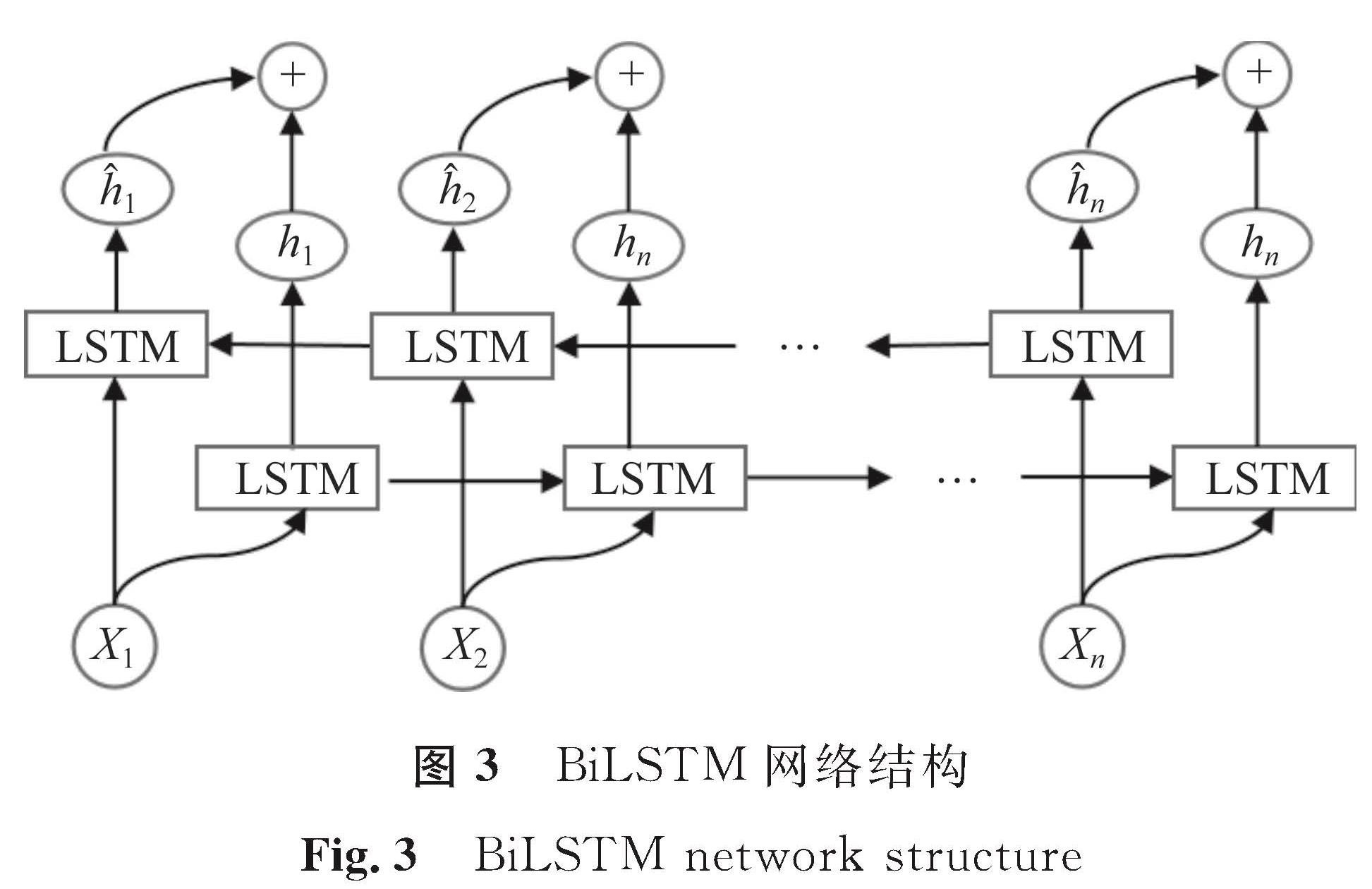
生成器G结构主体采用双向长短期记忆网络,该网络具有优良的金融时间序列数据处理能力,BiLSTM网络结构如图3所示,其中X表示输入量。BiLSTM由前向LSTM与后向LSTM组合而成,最终每个时间步i输出hi=[hi·hi],[·]表示拼接操作,即如果LSTM的隐含层维度是50,那么BiLSTM的维度则为100。经过多次试验后发现,单循环层为100个神经元时LSTM生成器模型预测效果较好,此时BiLSTM神经元数为200。
LSTM是一种在长期信息学习中表现出优越性的基本深度学习模型,其内部单元设计了输入门、输出门与遗忘门等结构,通过各个门对保存在细胞状态中的长期信息进行修改来实现选择性记忆与遗忘信息。LSTM内部单元结构如图4所示。
LSTM内部单元更新信息过程如下:
ft=σ(Wf×[ht-1,xt]+bf); (2)
it=σ(Wi×[ht-1,xt]+bi); (3)
c ~t=tanh(Wc×[ht-1,xt]+bc); (4)
ct=ft×ct-1+it×c ~t; (5)
ot=σ(Wo×[ht-1,xt]+bo); (6)
ht=ot×tanh(ct)。 (7)
式(2)~(7)中:σ为sigmoid激活函数; tanh为tanh激活函数; xt为单元输入向量; ht-1为上一时刻记忆单元的输出; ft表示遗忘门,用于决定丢弃细胞状态中哪些信息; Wf与bf分别为遗忘门的权重与偏置项; i表示输入门,用于决定哪些信息需要添加到细胞状态中; Wi与bi分别为输入门的权重与偏置项; c ~t为备选值向量,用于添加到新的细胞状态中; ct表示通过遗忘门与输入门更新细胞状态的过程; o表示输出门,用于决定输出细胞状态中哪些信息。Wo与bo分别为输出门的权重与偏置项; ht为该时刻记忆单元的输出。
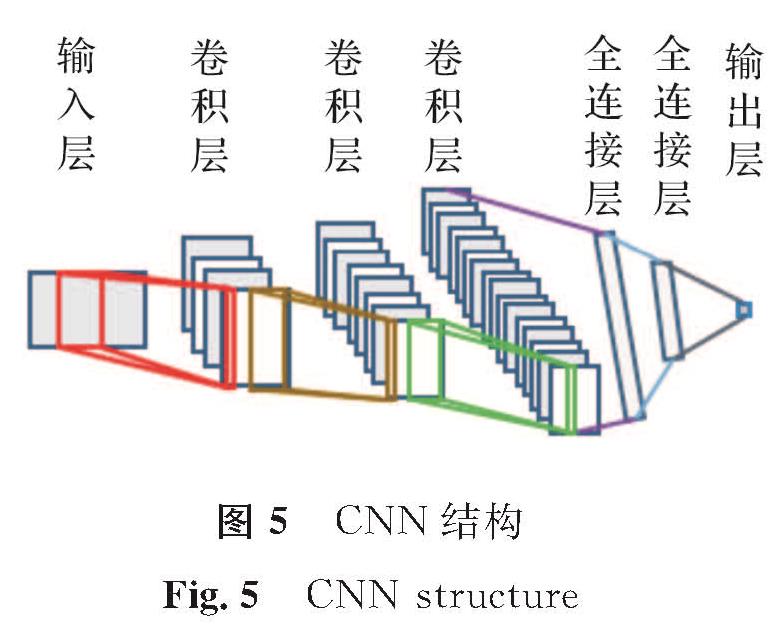
1.2.2 判别器判别器D结构主体采用CNN,经多次试验后发现,三层卷积层与两层全连接层的CNN效果最佳。其中每个卷积层依次有64、128、256个卷积核,卷积核尺寸为5×2与3×2两种规格,卷积按照2步进行,全连接层为两层,每层为220个神经元,CNN结构如图5所示。
CNN是一类带有卷积结构的深度前馈人工神经网络,由输入层和输出层及多个隐含层组成,其隐含层通常由卷积层、池化层与全连接层组成[26]。卷积层通过卷积核进行特征提取的过程可以表示如下:

式(8)中:hj,k为提取到的特征; Wl,m与b分别为共享权重与偏置量; L与M分别为局部感受野的长和宽; αj+l,k+m为卷积层接收到的数据。通过卷积层抽取特征后,再经全连接层进行分类得到输出项。
1.2.3 对抗训练在实际操作中,生成器与判别器交替优化:1)优化判别器D,将真实数据与样本数据输入D中,最大化D的判别准确率; 2)优化生成器G,将数据输入G中,最小化D的判别准确率。
本文模型的迭代次数设为1 000次,批处理大小设为128,学习率设为0.000 1,优化器采用Adam,它可以动态调整模型中参数的学习率。由此生成的样本数据质量与模型收敛速度都有很大的提高。为清楚起见,我们使用SGD(stochasticgradient descent,随机梯度下降法)进行迭代,批处理大小设置为1,然后通过对样本的损失求和将该算法推广到批处理大小为k。
设(X,Y)为数据集样本,为了使判别器D尽可能地判断不出数据来源,生成器G应减少对抗性损失。G的对抗性损失:

式(9)中:Y^为预测值; Lsce为sigmoid交叉熵损失,定义如下:
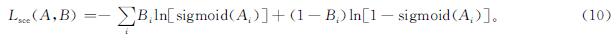
式(10)中:Ai为判别器输出特征; Bi为Ai对应的标签。
但实践证明仅将对抗性损失最小化并不能保证生成样本无限接近真实数据。为解决这个问题,生成器G还应减少预测误差损失Lp,其定义如下:

式(11)中:p=1或p=2; Y是真实值。此外,我们定义方向预测损失函数Ldpl如下:
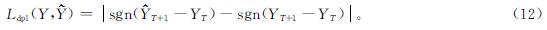
将上述定义的3项损失与参数λadv,λp与λdpl相结合就得到G的最终损失LG如下:
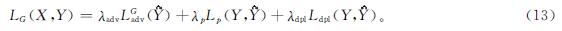
保持D权重不变,迭代G使LG(X,Y)最小化。
设(X,Y)为不同的数据样本,由于D只是为了确定输入序列是Y还是Y^,目标损失等于D上的对抗性损失。当G权重保持不变时,迭代D使目标损失LD最小化:
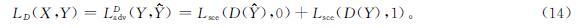
按照上述步骤交替训练生成器与判别器,最终生成器生成的数据无限接近真实数据,当判别器无法准确判断出数据来源时,训练结束。
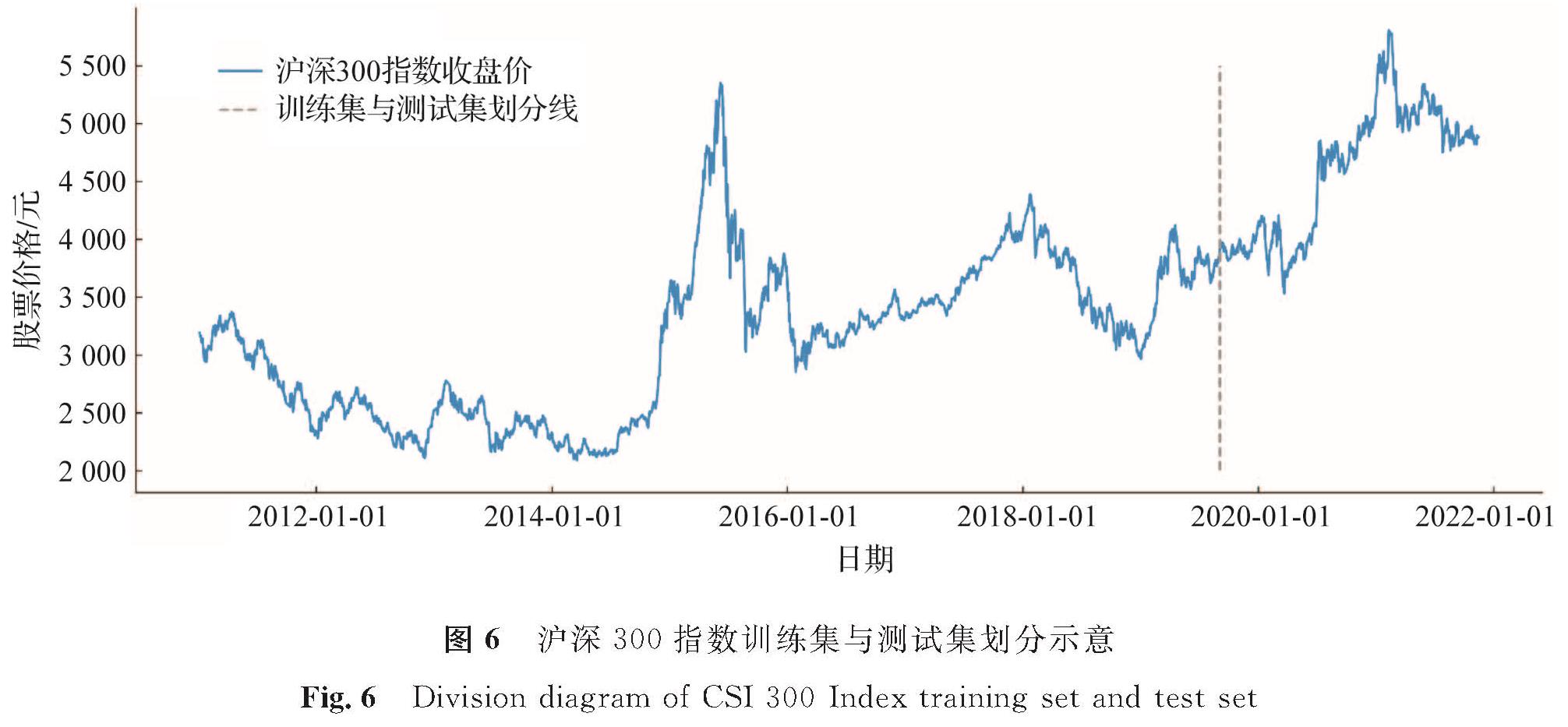
2 实证分析2.1 数据来源以沪深300指数为主要研究对象,利用多时间尺度GAN_BiLSTM模型预测下一交易日股价涨跌方向,然后使用大众熟悉且历史股价稳定的建设银行与陕西煤业两只股票数据用于验证模型有效性。股票交易信息来源于同花顺终端iFinD,选取2011年1月1日到2021年11月15日的沪深300指数日交易和15 min交易数据:包括开盘价、收盘价、最高价、最低价与交易量。其中,日交易数据有2 641条,15 min交易数据有42 256条。把要输入模型中的数据按照1.2节所述方法进行预处理。沪深300指数训练集与测试集划分示意如图6。在日交易尺度与15 min交易尺度上设置时间步长分别为20与16,即利用交易日前20日收盘价结合交易时间前16个15 min收盘价预测下一交易日收盘价涨跌方向。进行数据预处理之前,通过原始数据生成对应时间尺度的相关技术指标数据及基于ARIMA降噪后的预测价格,以便尽可能多地挖掘该股票的有效信息。
2.2 模型评价指标与基准模型
本研究选用均方误差(mean square error,MSE)、均方根误差(root mean square error,RMSE)及分类任务评价指标中的准确率、精确率、召回率与F1值作为模型预测效果的评价指标。其中,准确率指预测正确样本数占总体样本数的比例; 精确率指预测将要上涨样本中实际上涨样本所占的比例; 召回率指实际上涨样本中预测将要上涨样本所占的比例; F1值指精确率与召回率的调和平均。MSE与RMSE为数值预测评价指标,其计算公式分别如下:
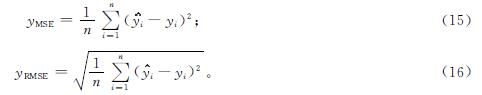
式(15)~(16)中: 为预测值; {y1,y2,…,yn}为真实值。就预测值而言,MSE与RMSE越小,预测误差越小,模型的预测效果也就越好; 反之效果越差。就预测涨跌方向而言,准确率、精确率、召回率与F1值越高,模型预测效果越好; 反之预测效果越差。
为预测值; {y1,y2,…,yn}为真实值。就预测值而言,MSE与RMSE越小,预测误差越小,模型的预测效果也就越好; 反之效果越差。就预测涨跌方向而言,准确率、精确率、召回率与F1值越高,模型预测效果越好; 反之预测效果越差。
为了更好地评价本文模型的预测效果,选用GRU、LSTM、GAN_GRU(generative adversarial networks based on gated recurrent units,基于门控循环单元的生成式对抗网络)与GAN_BiLSTM作为基准模型进行对比研究。
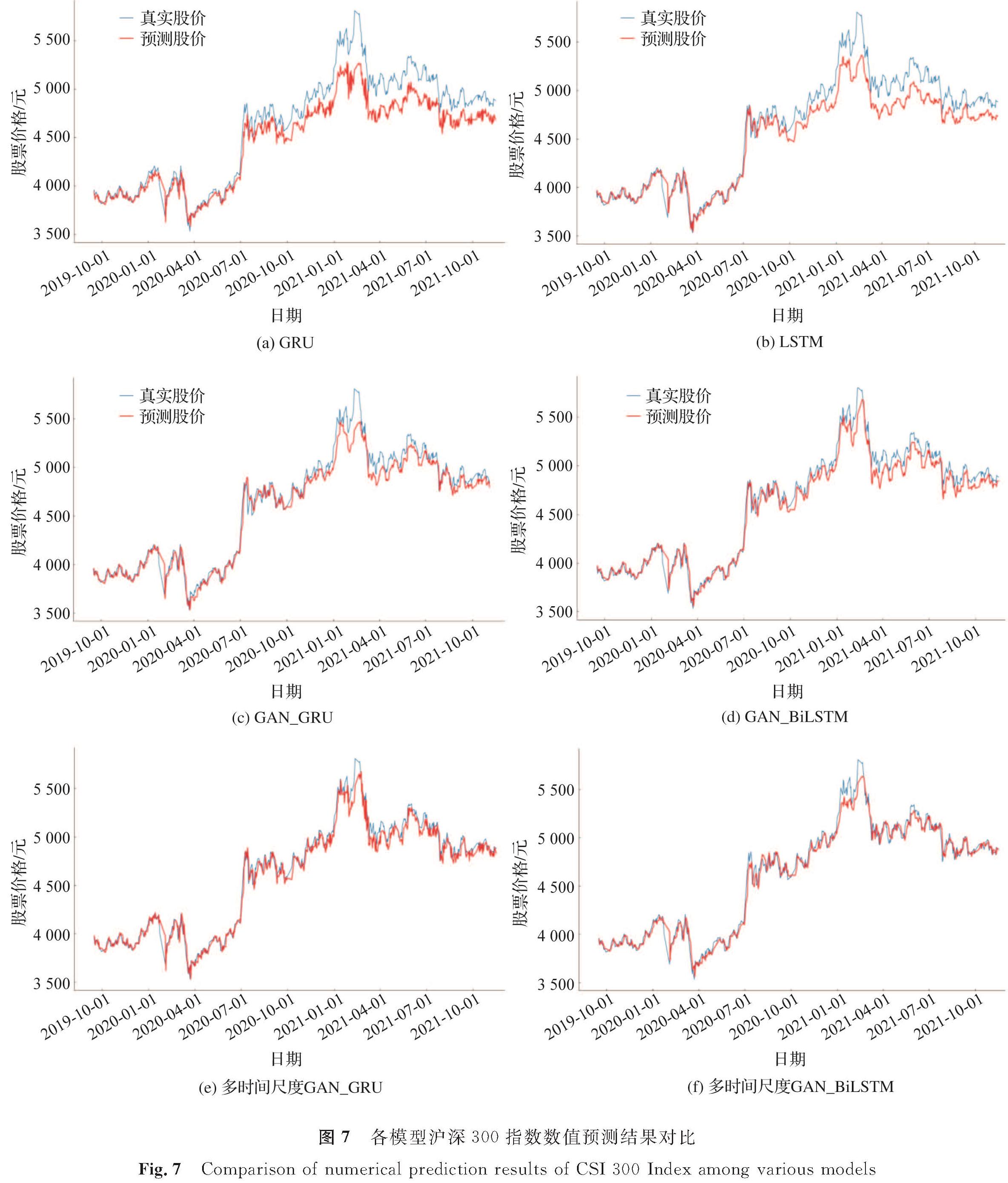
2.3 试验分析本文模型主要用于预测沪深300指数在下一交易日的涨跌方向,但为了凸显多时间尺度GAN_BiLSTM的预测优势,先利用各模型对沪深300指数下一交易日价格进行预测,将预测结果分别与股价真实值做对比,如图7所示。
图7 各模型沪深300指数数值预测结果对比
Fig.7 Comparison of numerical prediction results of CSI 300 Index among various models
由图7可知,基于GAN模型的数值预测效果明显优于GRU与LSTM,且多时间尺度信息结合GAN能有效提高模型预测能力,这说明运用多时间尺度GAN_BiLSTM模型预测股票价格具有可行性。
股票数据时间步长是模型预测效果的重要影响因素之一,若时间步长太小,则数据因包含有效信息太少而不能充分提取特征; 若时间步长太大,则会造成数据冗余与更严重的梯度消失问题。试验分别使用5、10、20、30、40、50时间步长日数据与8、16、32、48、64时间步长15 min数据组合来探索时间步长对预测效果的影响。通过各组合下准确率的比较,可知(20,16)时间步长组合预测效果优于其他时间步长组合。因此使用前20 d日交易数据与前16步15 min交易数据预测下一交易日股票价格涨跌,各模型沪深300指数预测结果评价指标对比见表2。
表2 各模型沪深300指数预测结果评价指标对比
Table 2 Comparison of evaluation indicators for prediction results of CSI 300 Index among various models
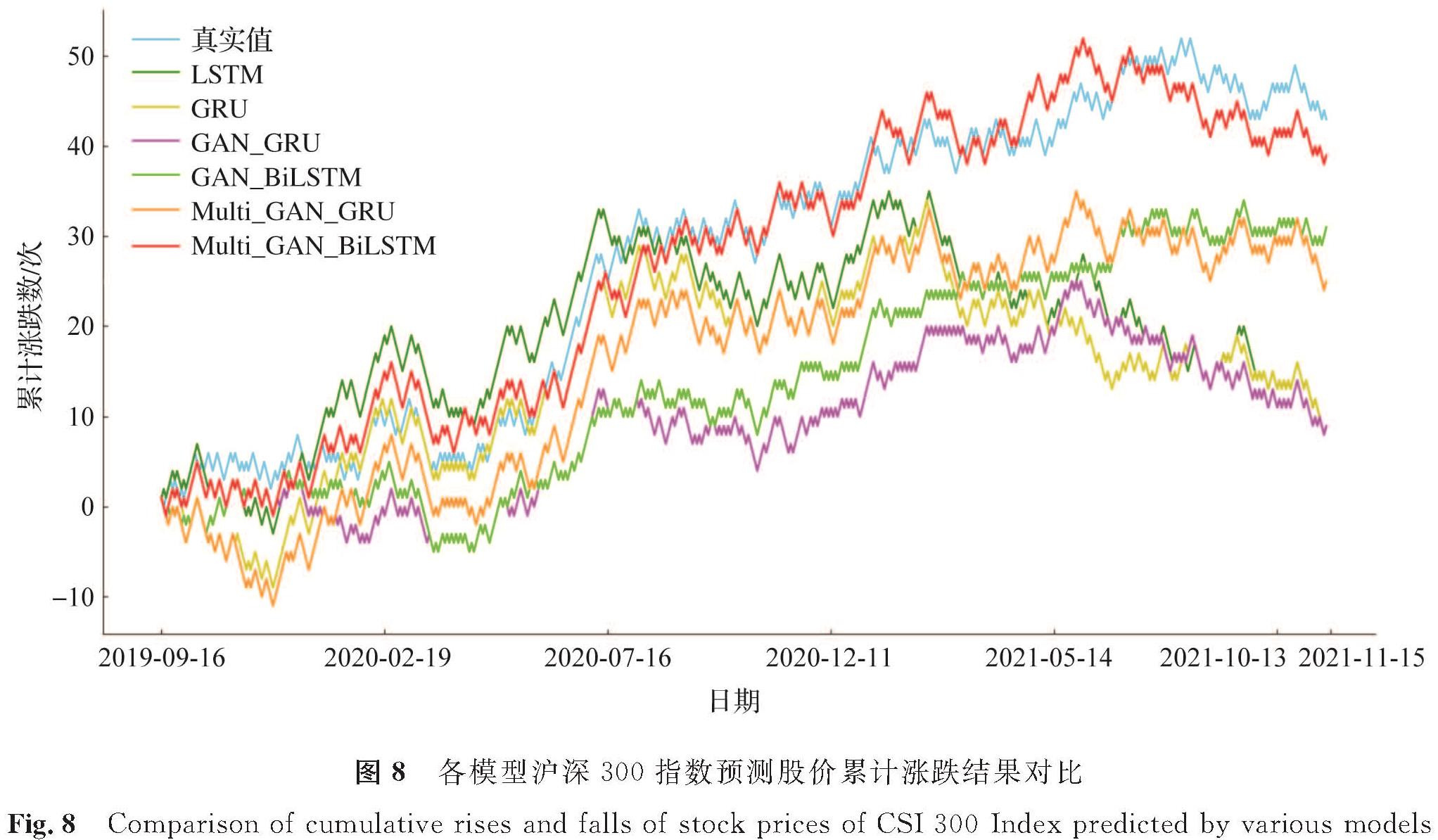
由表2可知,多时间尺度GAN_BiLSTM模型的MSE、RMSE数值均小于其他模型,此时其准确率、精确率、召回率与F1值分别为59.63%、59.24%、59.63%、59.43%,这些指标值均高于其他对比模型,这说明该模型涨跌趋势预测效果最好。此外,我们还发现,GAN用于股票价格涨跌预测优于一般深度神经网络,多时间尺度数据的引入更有助于预测精度的提高。各模型沪深300指数预测股价累计涨跌结果对比如图8所示,从图中可知,多时间尺度GAN_BiLSTM累计涨跌趋势与真实值变化情况最接近。
图8 各模型沪深300指数预测股价累计涨跌结果对比
Fig.8 Comparison of cumulative rises and falls of stock prices of CSI 300 Index predicted by various models
从上述结果来看,多时间尺度GAN_BiLSTM模型不论是沪深300指数价格预测还是涨跌方向预测均优于其他对比模型,从而说明本研究提出的模型具有一定的稳定性。此外,从本文模型微调参数后分别对建设银行与陕西煤业的股票收盘价预测结果来看,本研究提出的多时间尺度GAN_BiLSTM模型均表现出一定的优越性。
3 结 论股价走势是一个极为复杂的动力学系统,一直以来都是金融领域研究的重点和难点问题。本研究提出了多时间尺度GAN_BiLSTM模型,选取沪深300指数结合个股(建设银行与陕西煤业)股价数据进行试验。结果表明该模型的沪深300指数涨跌预测准确率为59.63%,比基准模型预测性能更好。今后的工作将尝试运用自然语言处理进行文本挖掘以提取情感指标,然后把股票时序特征与情感特征相结合,输入GAN模型以进一步提高预测准确率,还可尝试更多行业的股票数据以优化模型及其参数,从而探索本模型对金融领域时间序列的普适性。
- [1] AL-HMOUZ R, PEDRYCZ W, BALAMASH A. Description and prediction of time series: a general framework of granular computing[J].Expert Systems with Applications,2015,42(10):4830.
- [2] BARAK S, MODARRES M. Developing an approach to evaluate stocks by forecasting effective features with data mining methods[J].Expert Systems with Applications,2015,42(3):1325.
- [3] BOOTH A, GERDING E, MCGROARTY F. Automated trading with performance weighted random forests and seasonality[J].Expert Systems with Applications,2014,41(8):3651.
- [4] MARSZAEK A, BURCZYSKI T. Modeling and forecasting financial time series with ordered fuzzy candlesticks[J].Information Sciences,2014,273:144.
- [5] NAJAFABADI M M. Deep learning applications and challenges in big data analytics[J].Journal of Big Data,2015,2(1):1.
- [6] FAMA E F. The behavior of stock-market prices[J].The Journal of Business,1965,38(1):34.
- [7] SHLEIFER A, VISHNY R W. The limits of arbitrage[J].The Journal of Finance,1997,52(1):35.
- [8] GROSSMAN S J, STIGLITZ J E. On the impossibility of informationally efficient markets[J].The American Economic Review,1980,70(3):393.
- [9] JEGADEESH N, TITMAN S. Returns to buying winners and selling losers: implications for stock market efficiency[J].The Journal of Finance,1993,48(1):65.
- [10] LO A W. Reconciling efficient markets with behavioral finance: the adaptive markets hypothesis[J].Journal of Investment Consulting,2005,7(2):21.
- [11] YADAV S, SHARMA N. Forecasting of Indian stock market using time-series models[M]//Computing and Network Sustainability. Singapore: Springer,2019:405.
- [12] DEVI B U, SUNDAR D, ALLI P. An effective time series analysis for stock trend prediction using ARIMA model for nifty midcap-50[J].International Journal of Data Mining & Knowledge Management Process,2013,3(1):65.
- [13] 张贵生,张信东.基于近邻互信息的SVM-GARCH股票价格预测模型研究[J].中国管理科学,2016,24(9):11.
- [14] 王淑燕,曹正凤,陈铭芷.随机森林在量化选股中的应用研究[J].运筹与管理,2016,25(3):163.
- [15] MAO S, CHING P C, LEE T. Enhancing segment-based speech emotion recognition by iterative self-learning[J].IEEE/ACM Transactions on Audio, Speech, and Language Processing,2021,14(8):1.
- [16] 白翔,庞彦伟,章国锋.计算机视觉中的深度学习专题(2020)简介[J].中国科学:信息科学,2020,50(2):303.
- [17] JI H G, OH S, KIM J, et al. Integrating deep learning and machine translation for understanding unrefined languages[J].Computers Materials & Continua,2022,70(1):669.
- [18] FISCHER T, KRAUSS C. Deep learning with long short-term memory networks for financial market predictions[J].European Journal of Operational Research,2018,270(2):654.
- [19] 杨青,王晨蔚.基于深度学习LSTM神经网络的全球股票指数预测研究[J].统计研究,2019,36(3):65.
- [20] 乔若羽.基于神经网络的股票预测模型[J].运筹与管理,2019,28(10):132.
- [21] GOODFELLOW I, WARDE-FARLEY D, COURVILLE A, et al. Generative adversarial networks[J].Advances in Neural Information Processing Systems,2014,27:7.
- [22] SYED A. Forecasting pedestrian trajectory using deep learning[D].Las Vegas: University of Nevada,2021:48.
- [23] ZHANG K, ZHONG G, DONG J, et al. Stock market prediction based on generative adversarial network[J].Procedia Computer Science,2019,147:400.
- [24] 温玉莲,林培光.基于行业背景差异下的金融时间序列预测方法[J].南京大学学报(自然科学),2021,57(1):90.
- [25] 许飞飞,胡月,汪召兵.基于生成式对抗网络的股价预测研究[J].浙江科技学院学报,2022,34(3):210.
- [26] 卢强,朱振方,徐富永,等.融合语法规则的Bi-LSTM中文情感分类方法研究[J].数据分析与知识发现,2019,3(11):99.
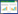 图 1 多时间尺度GAN_BiLSTM模型结构
Fig.1 Multi-time scale GAN_BiLSTM model structure
图 1 多时间尺度GAN_BiLSTM模型结构
Fig.1 Multi-time scale GAN_BiLSTM model structure