随着全球经济的发展、医疗水平的提高及生活条件的改善,各国人口死亡率逐渐降低,老龄化问题日益严重。在全球人口老龄化的背景下,死亡率的动态演变对人寿保险、养老基金、公共政策和财政规划等领域提出了巨大的挑战,特别是对于保险公司,养老金计划和人寿保险产品的定价需要准确预测未来死亡率。为此,研究者们提出了一系列的死亡率模型来拟合和预测死亡率。一般而言,死亡率模型分为确定型死亡率模型和随机死亡率模型[1-2]。但确定型死亡率模型只考虑了死亡率随年龄的变化规律,没有反映未来死亡率的不确定性,难以用于死亡率的准确预测。因此,随机死亡率模型在国内外得到了广泛研究,最为流行的是Lee-Carter系[3-5]模型和Carins-Blake-Dowd系[6-7]模型,Lee-Carter系模型形式简单、易于运用,Carins-Blake-Dowd系模型适用于高年龄人群。但这些离散随机死亡率模型通常需要对变量之间进行额外的假设,在长寿风险的情况下,直接对死亡强度建模更简单,故连续随机死亡率模型得到发展。Milevsky等[8]于2001年首次提出了一个连续随机死亡率模型,该模型是Gompertz生存函数的随机演化形式,被称为Milevsky-Promislow模型。Biffis[9]则提出利用仿射跳跃扩散过程对死亡强度进行建模,这种模型的形式更为简单且易于推导。Giacometti等[10]基于Milevsky-Promislow模型进行拓展,根据意大利死亡率数据说明拓展模型的拟合效果优于Milevsky-Promislow模型。国内这方面的研究文献尚不多,其中,尚勤等[11]使用带跳的Feller过程对死亡强度进行建模,发现该模型能够较好地模拟中国人口生存概率的变化趋势。孙荣[12]则在该模型的基础上,提出使用离散化方法估计模型参数,从而对死亡率进行预测,发现该方法具有较高的预测精度。
近几年,一些研究者给出了死亡率数据中存在长记忆性的经验证据,并基于已有的死亡率模型构建了长记忆性死亡率模型。长记忆性指一个随机过程在长时间内表现出持久行为的性质。在离散随机死亡率模型方面,Yan等[13]根据16个国家的死亡率数据,证实了不同年龄、性别和国家的数据中都存在长记忆性,并提出了基于Lee-Carter模型的长记忆性死亡率模型,实证结果表明忽略长记忆性的死亡率模型往往会低估预期寿命。在连续随机死亡率模型方面,Delgado-Vences等[14]用几何型分数Ornstein-Uhlenbeck过程对死亡率数据建模,并比较了估计Hurst指数的R/S分析(rescaled range analysis,重标极差分析)法、改进R/S分析法和Whittle法,结果显示R/S分析法估计的参数更加稳定。
这些研究表明,长记忆性的存在提高了对死亡率特征的理解,考虑长记忆性的死亡率模型能提高死亡率的拟合预测效果。另外,已有的长记忆性死亡率模型都只分析了年龄组死亡率的变化趋势,但死亡率模型的实际应用将涉及个体死亡率[15]的动态演变。因此,本研究基于长记忆特性拓展了Milevsky-Promislow死亡率模型,并称其为长记忆性Milevsky-Promislow模型; 然后利用死亡强度与死亡率的关系,通过对模型参数进行估计,探讨该模型对个体死亡率的拟合预测效果,并将其应用到中国寿险业经验生命表,为相关政策的制定提供参考。
1 死亡率模型介绍设(Ω,F,P)是一个概率空间,具有一个非降的σ-代数族{Ft:0≤t≤T}。年龄为x的个体在[t,T]时期的生存概率定义为

式(1)中:hx(u)为危险率函数,又称为死亡强度。所以对死亡强度进行建模,可以帮助解决寿险精算中的一些计算和理论研究问题。
1.1 Milevsky-Promislow模型假设x岁生存者的死亡强度过程是连续的均值回归布朗Gompertz过程,令hx(t)=h(t),那么死亡强度可以表示为

式(2)中:h0、g、σ为正常数; Yt为Ornstein-Uhlenbeck过程; Y0=0; b为非负常数; Wt为标准布朗运动。
1.2 长记忆性Milevsky-Promislow模型Milevsky-Promislow模型是基于标准布朗运动的随机过程来描述死亡强度,但间隔较久的死亡强度变化之间可能存在相关性,即时间序列具有长记忆性。最流行的长记忆建模方法是分数布朗运动,它已经被证实能较好地描述某些时间序列的长记忆性。因此,为了考虑长记忆性,自然可以利用分数布朗运动来代替Ornstein-Uhlenbeck过程中的布朗运动,此时死亡强度可表示为

式(3)中:YHt为分数Ornstein-Uhlenbeck过程; WHt为Hurst指数H(1/2<H<1)的分数布朗运动。
2 参数估计对于Milevsky-Promislow模型的参数估计研究直接使用序列二次规划法[10]221。而对于长记忆性Milevsky-Promislow模型的参数估计,本研究采用R/S分析法估计分数布朗运动中的Hurst指数,利用最小二乘法估计参数g,再使用Xiao等[16]的结论估计离散时间条件下分数Ornstein-Uhlenbeck过程的参数,具体做法如下。
令Xt=σYHt,则长记忆性Milevsky-Promislow模型可以写成

那么死亡强度方程就可以表示为
lnh(t)=lnh0+gt+Xt。
利用最小二乘法,参数g的估计量为
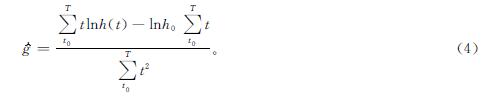
式(4)中:t0为观测起始年份; T为观测终止年份。
设n为样本量,h=1/n,tk=kh,k=1,2,…,n,在离散时刻(t1,t2,…,tn)观察到分数Ornstein-Uhlenbeck过程,为了简化符号,使用(X1,X2,…,Xn)代替(Xt1,Xt2,…,Xtn)表示观测到的时间序列样本。
那么当假设Hurst指数已知,且1/2<H<1时,参数σ的平方的估计量为
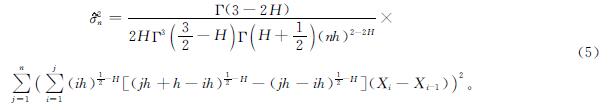
式(5)中: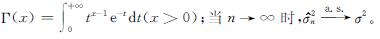
类似地,当1/2<H<3/4时,参数b的估计量为

式(6)中: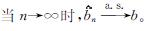
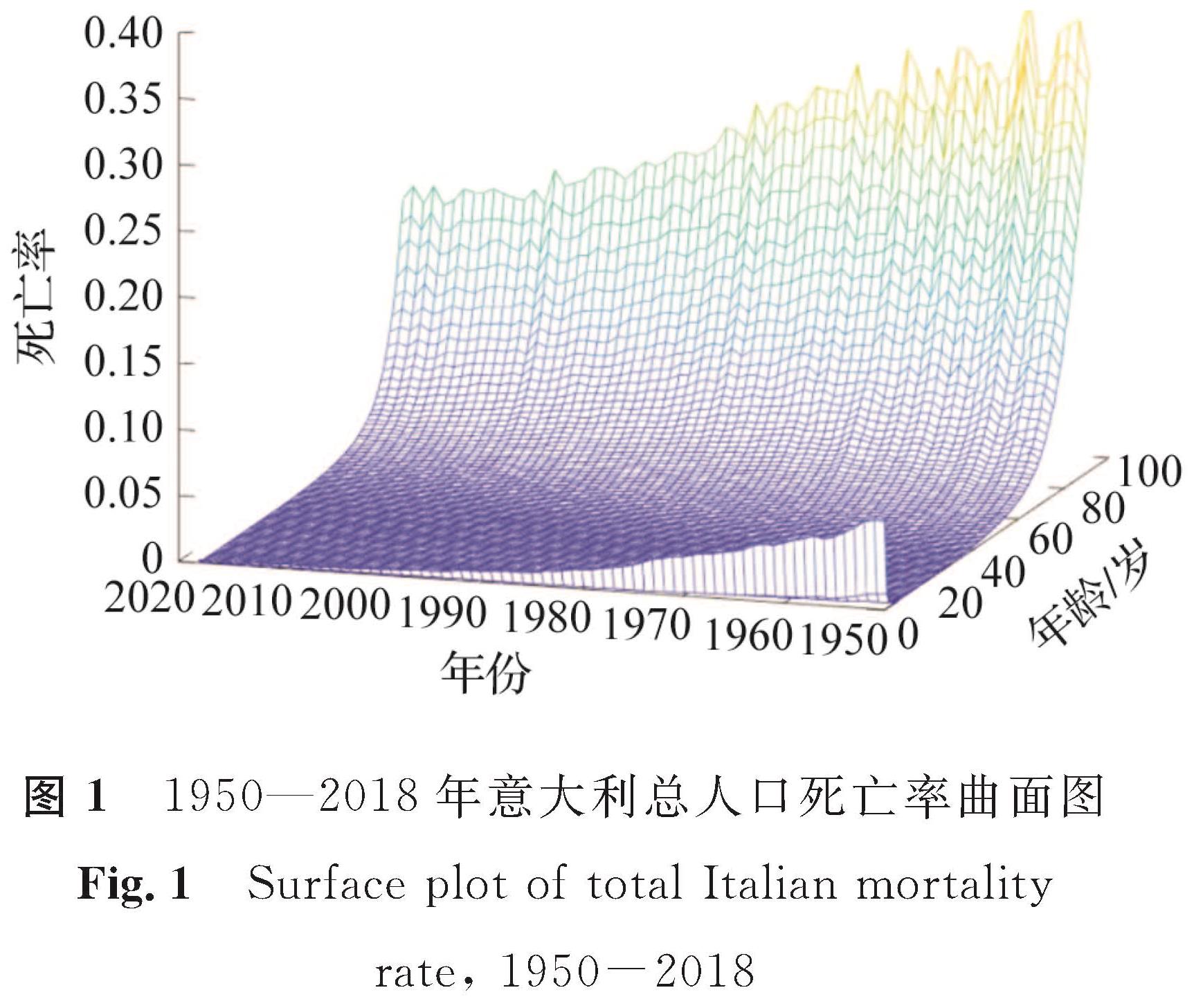
考虑到中国人口死亡率数据量较少且有缺失,而Milevsky-Promislow模型多采用意大利数据进行说明,故本研究选取意大利1950年至2018年不同年龄和性别的死亡率,数据来源于http://www.mortality.org。为了研究个体死亡率的随机演化,分别将总人口、男性人口、女性人口的死亡率数据构造成3个M×N维的矩阵A、B、C,其中M表示年龄x(0≤x≤91),N表示年份t(1950≤t≤2018),研究中使用矩阵的对角线数据。矩阵中的每个元素mx,t为在年份t时年龄为x的个体死亡率。对于年龄为x的个体,死亡强度ht=-ln(1-mx,t),利用一阶泰勒近似,则lnht=lnmx,t。根据矩阵A数据绘制1950—2018年意大利总人口死亡率曲面图(图1)。由图1可知,1950—2018年,死亡率整体呈下降的趋势,这反映了随着意大利生活水平和医疗条件的改善,人口寿命越来越长。另外,如果给定个体的初始年龄为x,数据将沿着对角线收集,死亡率会随着时间的推移而增加,因此长记忆性Milevsky-Promislow模型符合个体死亡率的演变趋势。
3.2 长记忆性的存在
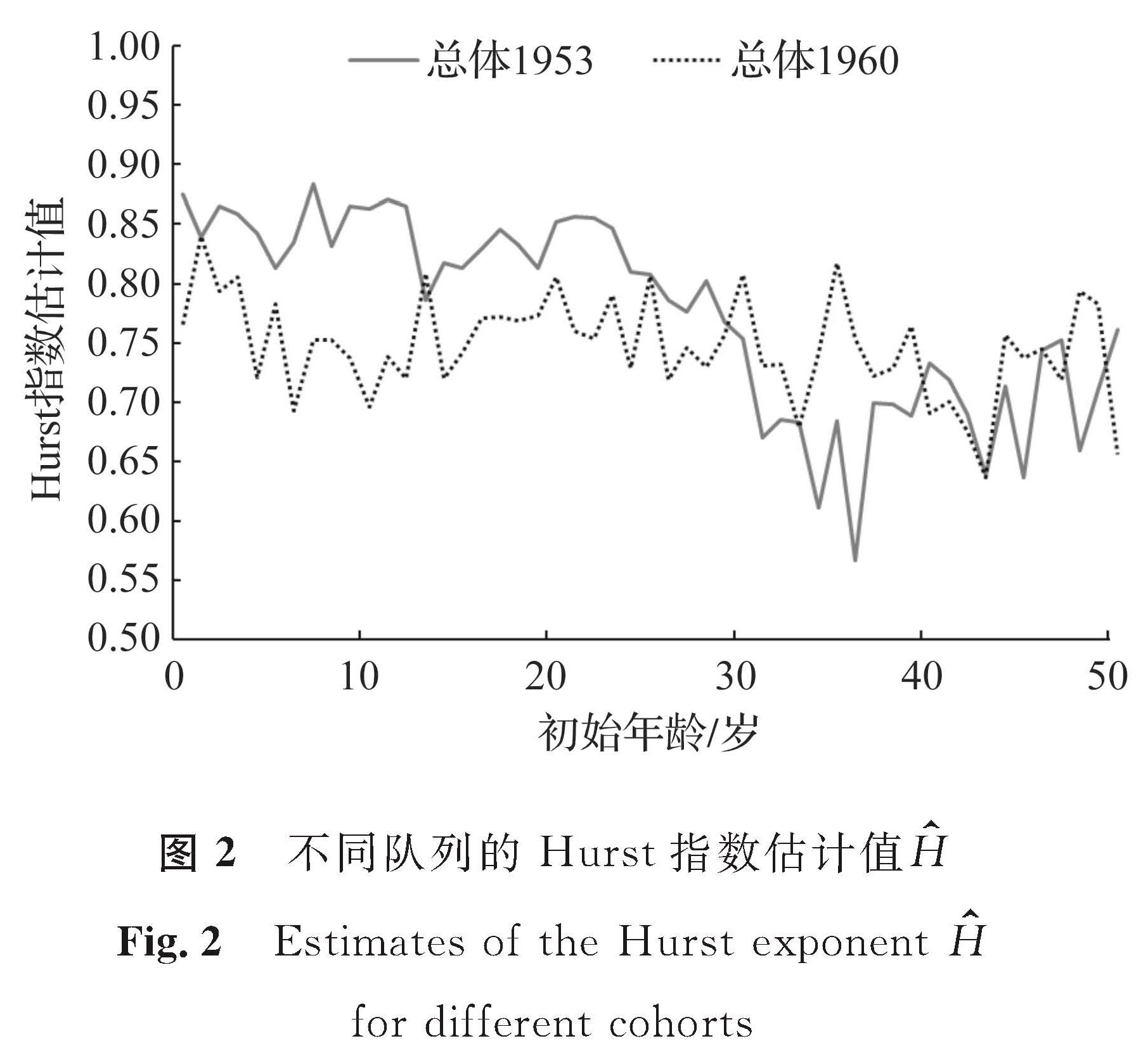
在上述数据矩阵A中选取t=1953和t=1960时观察到的不同初始年龄x(x=0,1,…,50)的个体死亡率队列来估计Hurst指数。不同队列的Hurst指数估计值如图2所示。不同年份不同初始年龄的个体的死亡率时间序列中都存在长记忆性。因此,在分析死亡率的随机演化时,考虑长记忆性的死亡率模型更具有现实意义。
3.3 模型拟合效果分析3.3.1 模型比较
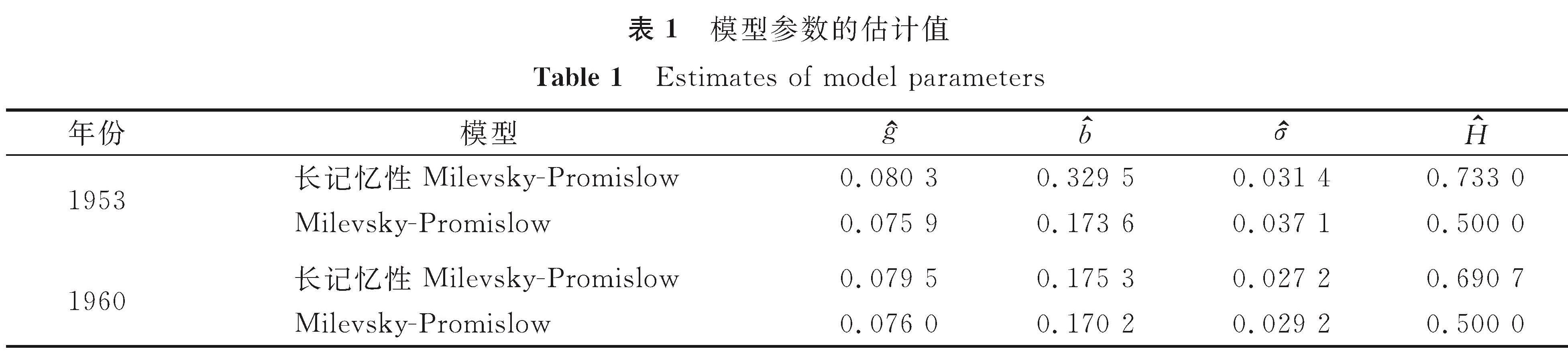
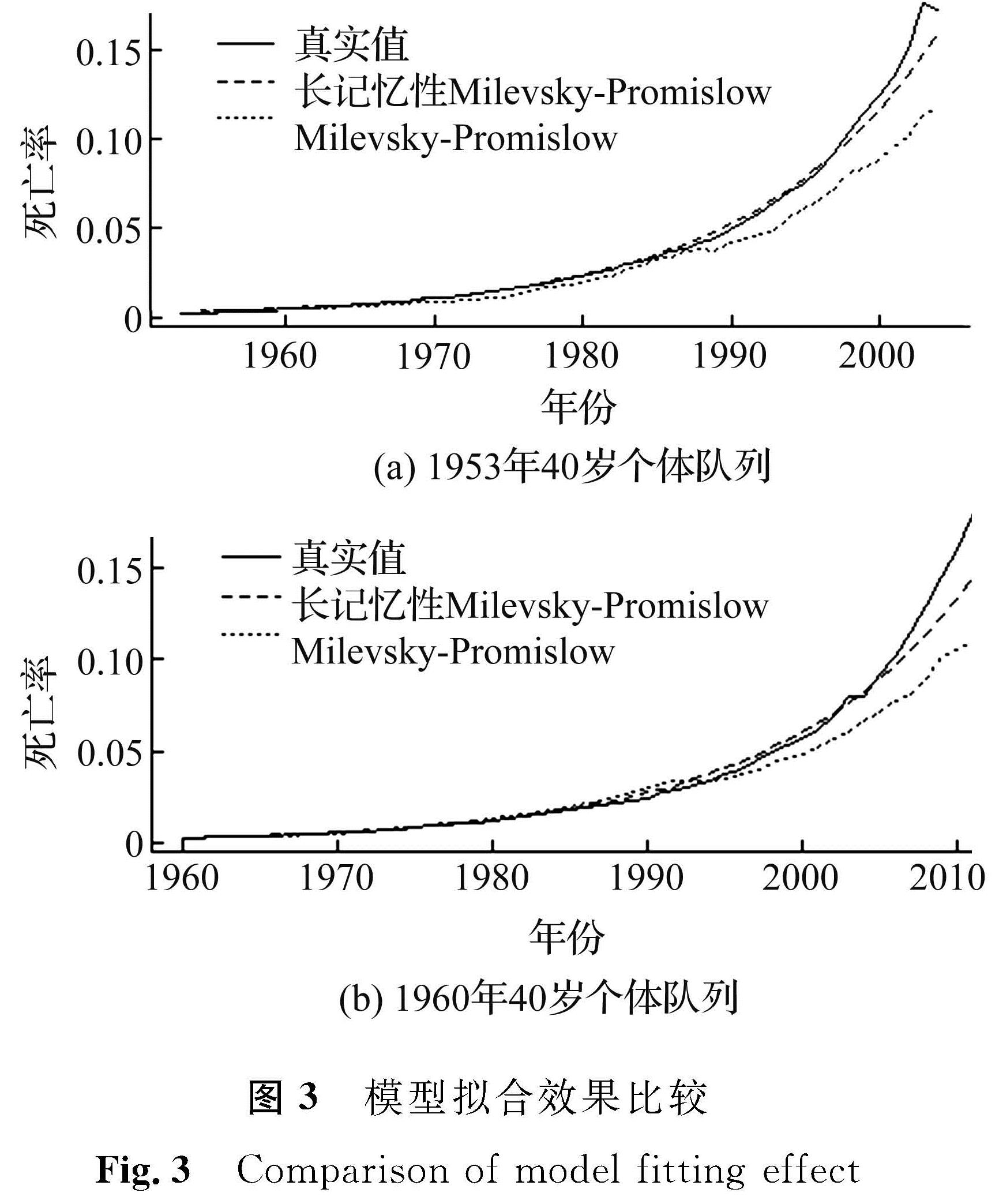
考虑到长记忆性的存在可能对模型的参数估计有所影响,在比较长记忆性Milevsky-Promislow模型和Milevsky-Promislow模型的拟合效果时,分别采用了不同的参数估计方法,并在1953—2004年的总人口死亡率数据中,选取了H ∈(0.5,0.75)的1953年和1960年40岁的个体队列进行比较。模型参数的估计值见表1。
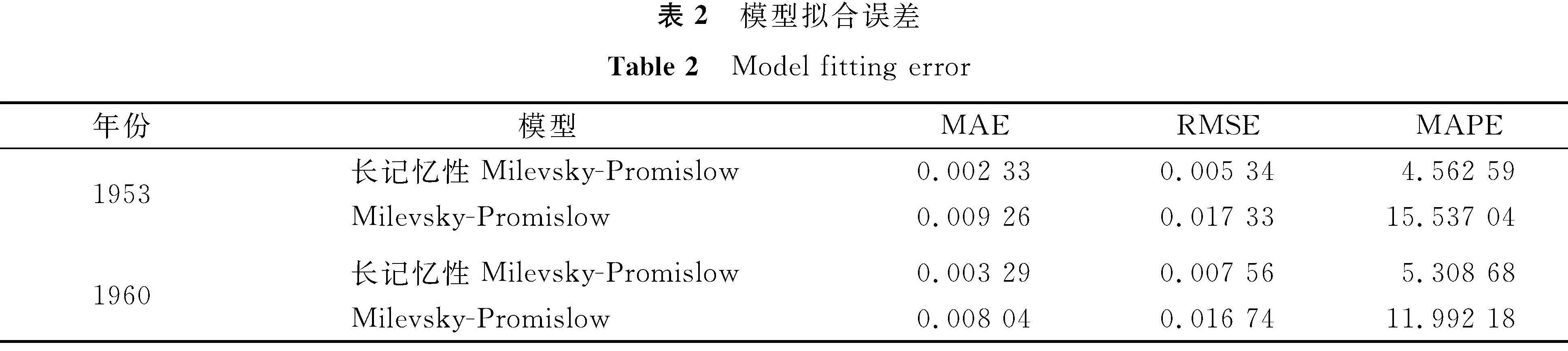
为了评估模型的拟合效果,采用3种误差标准:平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)和平均绝对百分误差(mean absolute percentage error,MAPE),模型拟合误差见表2。
根据表2,相对于Milevsky-Promislow模型,长记忆性Milevsky-Promislow模型中1953年队列的MAE、RMSE和MAPE分别降低了74.84%、69.19%和70.63%; 1960年队列的MAE、RMSE和MAPE则分别降低了59.08%、54.84%和55.73%。
为了更加直观地比较两个模型的拟合效果,绘制了模型拟合效果比较图(图3)。由图3可知:Milevsky-Promislow模型仅仅反映了个体死亡率的总体趋势,没有捕捉到时间序列的长记忆性; 而考虑长记忆性的死亡率模型,不仅反映了总体趋势,且拟合值比原模型更接近真实值,误差非常小。这意味着考虑死亡率时间序列中长记忆性的存在是非常有必要的。
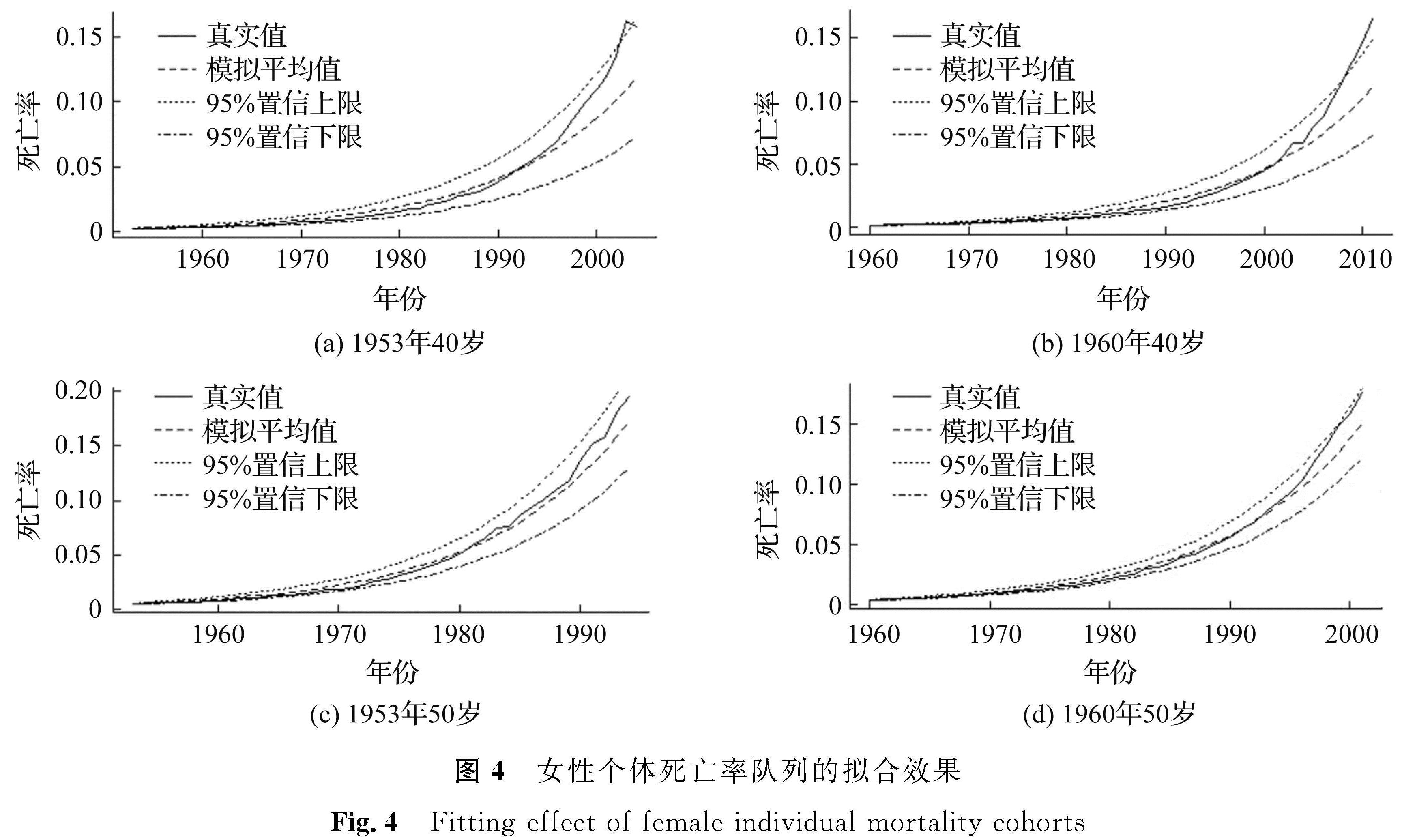
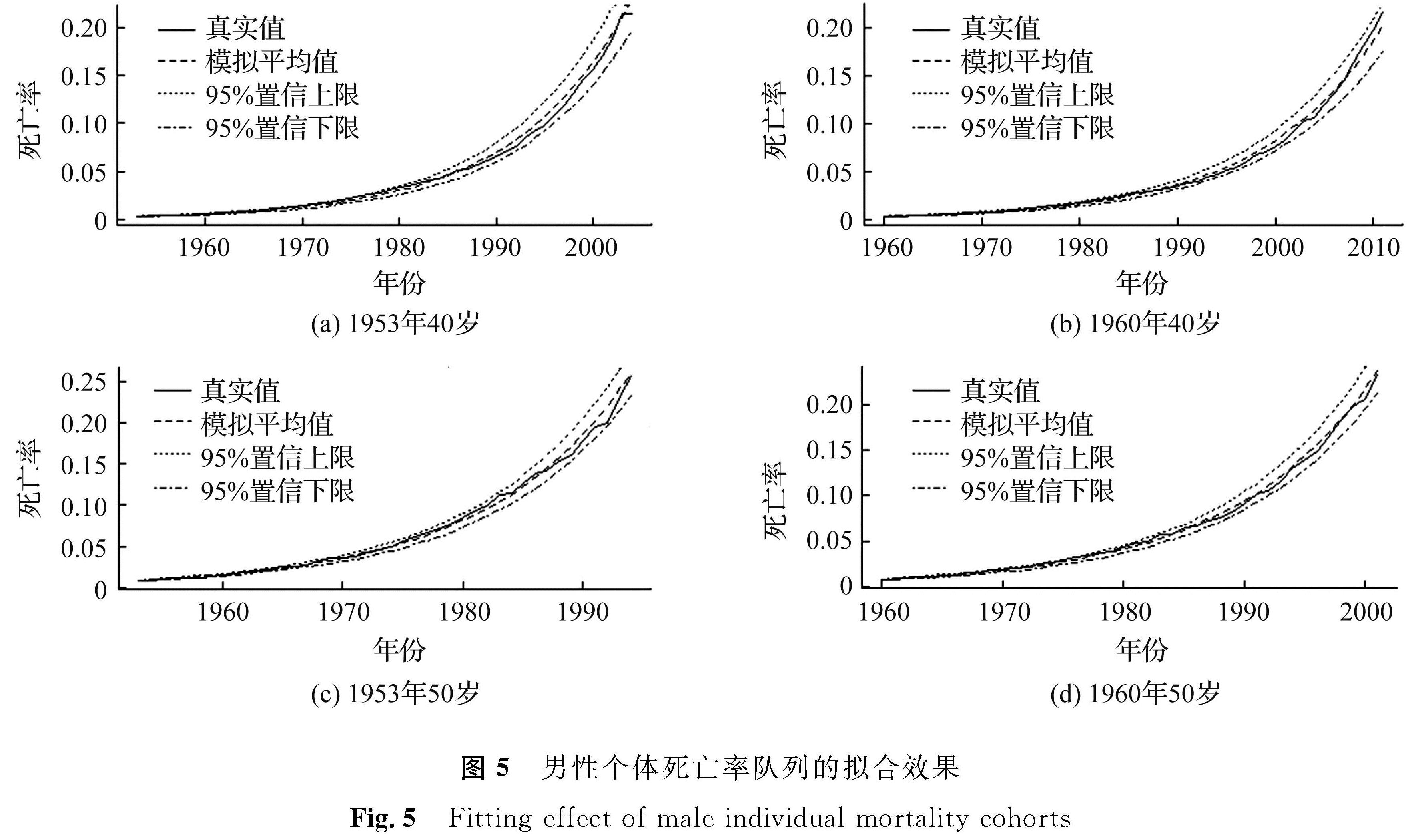
3.3.2 模型的适用性为研究长记忆性Milevsky-Promislow模型在不同性别和不同初始年龄的个体队列中的适用性,选择意大利人口男性和女性的死亡率数据矩阵,选取1953年和1960年初始年龄为40、50岁的男女队列进行分析。采用上述参数估计方法估计参数值,通过模拟分数布朗运动,进而模拟10 000条样本路径,得到每个个体队列的死亡率均值和95%置信区间。根据意大利女性和男性个体死亡率队列的历史死亡率、模拟平均值和95%置信区间绘制的拟合效果如图4和图5所示。
显而易见,长记忆性Milevsky-Promislow模型适用于图中所有队列,但男性队列的拟合效果总体优于女性队列。对1953年和1960年初始年龄为40岁的女性个体而言,死亡率被低估了,不过历史死亡率基本上保持在95%的置信区间内,这说明了拟合结果的可靠性。由于参数估计方法要求Hurst指数的范围为(0.5,0.75),该限制可能会导致对死亡率的低估。
同时,序列长度相同,初始年龄相同,但出生年份不同的队列,拟合效果相似,如1953年和1960年初始年龄为40岁的队列; 但初始年龄不同的队列,拟合效果有所差异。总体而言,长记忆性Milevsky-Promislow模型对死亡率总体趋势有着较为准确的估计,无论是男性个体还是女性个体,该模型都捕捉到了死亡率数据中的长记忆性,并显示了个体死亡率的变化趋势。
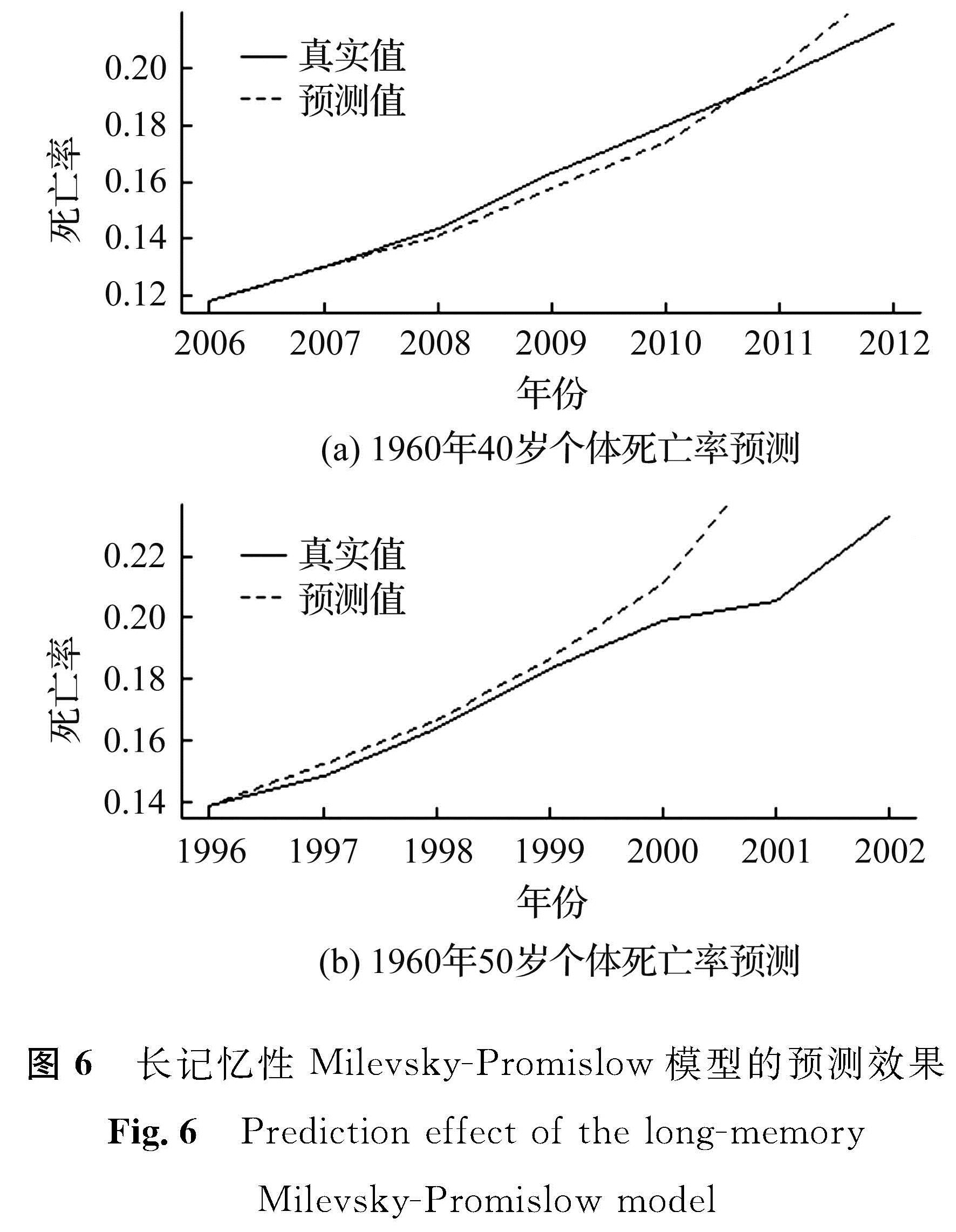
3.4 模型预测效果分析为了检验长记忆性Milevsky-Promislow模型的预测效果,选取意大利男性人口1960年初始年龄为40岁的个体死亡率数据,使用前46年(1960—2005年)数据进行参数估计,后7年(2006—2012年)数据进行回溯测试[17]; 选取男性1960年初始年龄为50岁的个体死亡率数据,使用前36年(1960—1995年)数据进行参数估计,后7年(1996—2002年)数据进行回溯测试,得到长记忆性Milevsky-Promislow模型的预测效果如图6所示。
图6显示了长记忆性Milevsky-Promislow模型预测值在回溯时间段内与真实值的对比,可以看出预测值在前几年非常接近真实数据,后几年误差渐大。这种静态预测使得预测后期误差加大,采用动态预测或将可以提高预测精度。总体而言,对于拟合效果较好的队列,长记忆性Milevsky-Promislow模型对其个体死亡率的预测也比较准确。该结果说明了长记忆性死亡率模型对死亡率预测有着较好的效果。
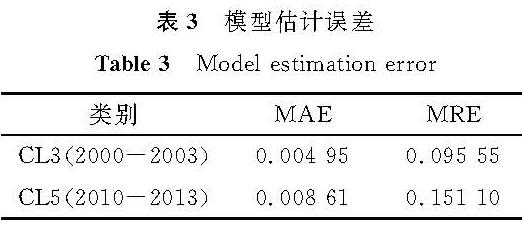
3.5 模型应用研究生命表是反映一批人从出生后陆续死亡的全部过程的一种统计表,与个体死亡率含义相同,在寿险精算中是研究死亡率变化的重要工具。为了对未来死亡率的变化趋势进行研究,分别利用《中国人寿保险业经验生命表(2000—2003)》中的养老金业务男表CL3(2000—2003)和《中国人寿保险业经验生命表(2010—2013)》中的养老金业务男表CL5(2010—2013)数据估计长记忆性Milevsky-Promislow模型的相关参数,对中国40岁男性各年生存率(生存率=1-死亡率)进行预测,将预测结果与实际各年生存率进行比较。预测精度评价指标采用MAE和平均相对误差(mean relative error,MRE),模型估计误差见表3。
从表3可以看出,模型对CL3(2000—2003)的估计效果比CL5(2010—2013)要好,不过都能够达到一定的精度。因此,利用长记忆性死亡率模型可以预测未来的死亡率,进而能够对长寿风险进行分析,为相关部门对养老保险制度的改革提供理论参考,以便更好地应对老龄化背景下的风险与挑战。
4 结 语本研究以意大利个体死亡率为基础,应用长记忆性Milevsky-Promislow模型拟合和预测死亡率。首先利用R/S分析法求出Hurst指数,并对模型的参数进行估计; 通过与Milevsky-Promislow模型对比,得出考虑长记忆性的死亡率模型的拟合效果优于原死亡率模型。因此,进一步使用长记忆性死亡率模型分析其拟合预测效果,并将本模型应用到中国寿险业经验生命表,实证结果表明本模型具有较为准确的估计结果。本研究为死亡率的估计方法和相关模型的发展提供了一定的理论支持。另外,虽然国内死亡率数据不足,但通过一定的数据处理方法,或能将长记忆性死亡率模型用于分析中国人口死亡率。
- [1] 王耀中,樊毅,张宁.长寿风险模型与管理研究新进展[J].湖南财政经济学院学报,2016,32(1):87.
- [2] 王晓军,路倩.动态死亡率模型的研究进展[J].应用概率统计,2020,36(4):415.
- [3] LEE R D, CARTER L R. Modeling and forecasting U.S. mortality[J].Journal of the American Statistical Association,1992,87(419):659.
- [4] 肖鸿民,马海飞,康彦玲.两种死亡率预测方法的比较[J].统计与决策,2020,36(23):5.
- [5] 胡月,陈岚岚,章迪平.基于Copula方法的Lee-Carter模型的长寿互换风险定价研究[J].浙江科技学院学报,2020,32(6):509.
- [6] CAIRNS A J G, BLACK D P, DOWD K. A two-factor model for stochastic mortality with parameter uncertainty: theory and calibration[J].Journal of Risk and Insurance,2006,73(4):687.
- [7] 吴晓坤,雒水稞,苏雯,等.中国人口CBD死亡率模型的参数再调整[J].统计与决策,2021,37(23):41.
- [8] MILEVSKY M A, PROMISLOW S D. Mortality derivatives and the option to annuitise[J].Insurance: Mathematics and Economics,2001,29(3):299.
- [9] BIFFIS E. Affine processes for dynamic mortality and actuarial valuations[J].Insurance: Mathematics and Economics,2005,37(3):443.
- [10] GIACOMETTI R, ORTOBELLI S, BERTOCCHI M. A stochastic model for mortality rate on Italian data[J].Journal of Optimization Theory and Applications,2011,149(1):216.
- [11] 尚勤,秦学志.随机死亡率和利率下退休年金的长寿风险分析[J].系统工程,2009,27(11):56.
- [12] 孙荣.运用带跳过程的死亡强度对死亡率的估计[J].系统工程,2021,39(1):43.
- [13] YAN H, PETERS G W, CHAN J. Mortality models incorporating long memory for life table estimation: a comprehensive analysis[J].Annals of Actuarial Science,2021,15(3):567.
- [14] DELGADO-VENCES F, ORNELAS A. Modelling Italian mortality rates with a geometric-type fractional Ornstein-Uhlenbeck process[DB/OL].(2019-01-03)[2021-10-01].
- [15] APICELLA G, DACOROGNA M, DI LORENZO E, et al. Improving the forecast of longevity by combining models[J].North American Actuarial Journal,2019,23(2):298.
- [16] XIAO W, ZHANG W, XU W. Parameter estimation for fractional Ornstein-Uhlenbeck processes at discrete observation[J].Applied Mathematical Modelling,2011,35(9):4196.
- [17] 肖鸿民,白爱琴,赵弘宇.基于CIR特性的高龄死亡率预测方法[J].西北师范大学学报(自然科学版),2021,57(6):7.
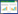 图 1 1950—2018年意大利总人口死亡率曲面图
Fig.1 Surface plot of total Italian mortality rate, 1950-2018
图 1 1950—2018年意大利总人口死亡率曲面图
Fig.1 Surface plot of total Italian mortality rate, 1950-2018