二分支链环L=L1∪L2称为二邻近于W=W1∪W2,假如存在L的两个交叉c1,c2,则改变其中任何1个或同时改变它们2个得到的都是W[1]767。对于定向的链环也有相似定义,本文假设所考虑的链环是有定向的。记实现二邻近的交叉的符号分别是α,β。D=D(oc1,oc2)是分别打开这两个交叉所得到的链环。进一步,根据二邻近的定义,以及文献[1]768的讨论可知,相关的2个交叉不可能是2个分支形成的交叉,不失一般性,假设改变c1后L1成为了W1,于是L2=W2,lk(L)=lk(W)[1]769(下文中我们均使用这些假设)。二邻近链环的概念从提出到现在也有将近20年的时间了,但二邻近链环的研究成果并不是很多,足见其研究有一定的难度。目前主要的研究结果是由文献[1]768-775和文献[2-5]给出的,其中特别是文献[1]768-770的研究,给出了一些判别一般链环间的二邻近性的方法和结果。与本研究相关的结果,读者可以参考命题1~5。本研究旨在提供二邻近链环应该满足的一个新的关系式,以此也作为前述文章的一个补充。
我们有以下结果:
定理 如上假设,且实现二邻近的2个相关交叉c1,c2分别在L的不同分支上,则a3(D)=λ2lk(L),λ∈Z。其中a3(D)是D的Conway多项式中z3的系数。
最后,将给出一个例子来说明这个定理的应用。这里假定读者已了解一些相关的基本知识,也可参考文献[6-7]。
1 基本知识假如G=L1∪L2∪L3∪L4是有4个分支的定向链环,记lk(Li,Lj)=lij,i≠j为2个不同分支之间的链环数,则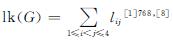 。
。
命题1[1]768,[9-10] 令a3(G)是链环G的Conway多项式Δ(G)(∈Z[z])中z3的系数,则
a3(G)=-l12l13l14-l12l23l14-l13l23l14-l12l13l24-l13l14l24-l12l23l24-l13l23l24-l14l23l24-
l12l13l34-l12l14l34-l12l23l34-l13l23l34-l14l23l34-l12l24l34-l13l24l34-l14l24l34。
命题2[1]768 如前假设,有
Δ(L)=αβz2Δ(D(oc1,oc2))+Δ(W)。
命题3[1]770,[11] 记号和假设如前,又假设V(G; t)(∈Z[t±1/2])(简记为V(G))是链环G的Jones多项式,c(G)是它的分支数,则
1)V'(G; 1)=-3(-2)c(G)-2lk(G);
2)V(D(oc1,oc2); t)=αβt1-α-β(V(L; t)-(t2α+t2β-t2(α+β))V(W; t))(1-t)-2。
命题4[1]769 记号和条件同上,lk(L)=lk(W)≠0,a3(L)=a3(W),则D(oc1,oc2)有4个分支。
命题5[1]770 记号和条件同上,若实现二邻近的2个交叉都在L1上,且D(oc1,oc2)有4个分支,则
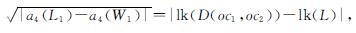
且假如L2与D(oc1,oc2)的任一不同于L2的分支的链环数都不为零,则a3(D(oc1,oc2))为(lk(D(oc1,oc2))-2lk(L))2lk(L); 否则为|a4(L1)-a4(W1)|lk(L)。
2 定理的证明如前假设,并假设交叉c1,c2分别在L1,L2上,L1打开c1后使其成为链环oc1=G1∪G2,L2打开c2后使其成为链环oc2=G3∪G4,ljk=lk(Gj∪Gk),于是a2(L1)-a2(W1)=lk(oc1)=l12。如果先改变c2,则有2种情形:
1)如果L2(=W2)变成W2,那么L1=W1,0=a2(L1)-a2(W1)=lk(oc1)=l12,0=a2(W2)-a2(W2)=lk(oc2)=l34。
2)如果L2(=W2)变成W1,那么W2=W1,L1=W2,即L1=W2=W1,也即0=a2(W2)-a2(W1)=lk(oc2)=l34,且0=a2(L1)-a2(W1)=lk(oc1)=l12。
所以无论哪一种情形,都有l12=0=l34,故
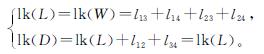
因L二邻近于W,所以
0=a3(L)-a3(W)=αa2(oc1,c2)=αa2(G1∪G2∪L2)=βa2(L1∪G3∪G4),
即
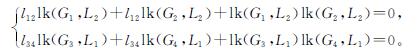
但lk(G1,L2)=l13+l14,lk(G2,L2)=l23+l24,l12=0,lk(G1,L2)+lk(G2,L2)=lk(L),lk(G3,L1)=l13+l23,lk(G4,L1)=l14+l24,l34=0,lk(G3,L1)+lk(G4,L1)=lk(L),故

也即
lk(L)=l13+l23,l14=-l24,或lk(L)=l14+l24,l13=-l23,
且
lk(L)=l23+l24,l13=-l14,或lk(L)=l13+l14,l23=-l24。
综合得,若L的其中1个分支A的交叉被打开后得2个分支,则lk(L)就等于A的其中1个分支与L中的另1个分支B的链环数,而A的另1个分支与L的另1个分支B的链环数为零。
下面来计算a3(D)。
根据命题1,因为l12=l34=0,所以
a3(D)=-l13l23l14-l13l14l24-l13l23l24-l14l23l24。
根据式(1),只能有以下4种情形:
1)lk(L)=l13+l23,l14=-l24,且lk(L)=l23+l24,l13=-l14,故
a3(D)=l213(l13+l23)=l213lk(L);
2)lk(L)=l13+l23,l14=-l24,且lk(L)=l13+l14,l23=-l24,故
a3(D)=-l214(l24-l13)=l214lk(L);
3)lk(L)=l14+l24,l13=-l23,且lk(L)=l23+l24,l13=-l14,故
a3(D)=l213(l24-l13)=l213lk(L);
4)lk(L)=l14+l24,l13=-l23,且lk(L)=l13+l14,l23=-l24,故
a3(D)=l213(l14-l23)=l213lk(L)。
这样就完成了定理的证明。
3 例 子
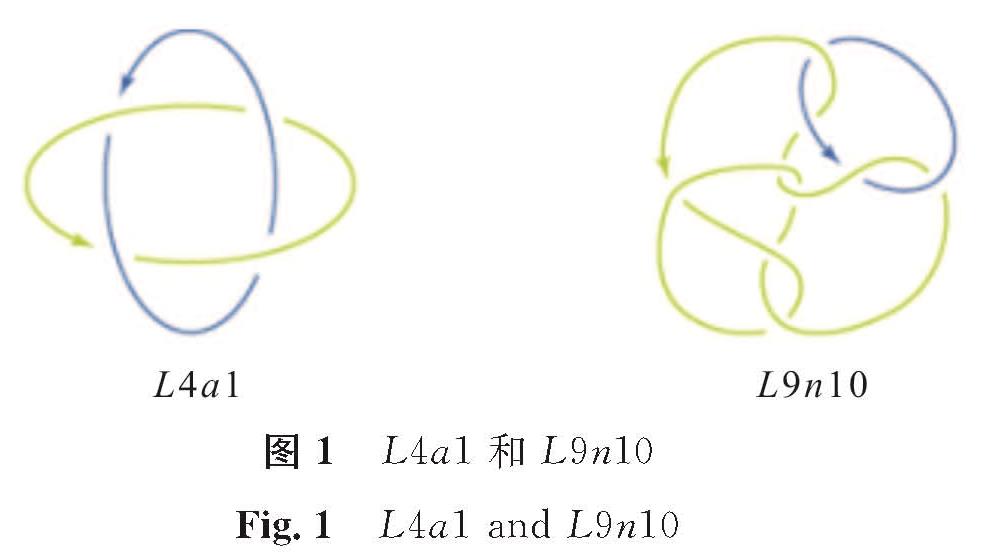
例:若定向的链环L4a1与L9n10如图1所示,则不可能通过改变2个异号的交叉使得前者二邻近于后者。
因Δ(L4a1)=z3+2z,Δ(L9n10)=z5+z3+2z,根据命题2,D的Conway多项式为(Δ(L4a1)-Δ(L9n10))z-2=-z3。由假设αβ=-1,知a3(D)=1,而且由命题4得知D有4个分支。
因V(L4a1)=-(1+t2-t3+t4)t-3/2,且
V(L9n10)=-t-5/2(-1+3t-4t2+5t3-5t4+5t5-3t6+2t7),
由命题3中的结论2)得,V(D; t)=-t(V(L4a1)-(t2+t-2-1)V(L9n10))(1-t)-2),所以V'(D; 1)=-24。由命题3中的结论1)得,lk(D)=2。如果c1,c2是L4a1的同一个分支的交叉,那么根据命题5,a3(D)应该等于(lk(D)-2lk(L))2lk(L)=8或者|a4(L1)-a4(W1)|lk(L)=0。显然,这都是不可能的。因此,c1,c2分别在不同的分支上。于是,根据上面的结论,得到a3(D)=2a2,a∈Z,这也是不可能的,因为a3(D)=1。
综上,L4a1不可能通过改变2个异号的交叉来实现二邻近于L9n10。
- [1] TAO Z X. On 2-adjacency between links[J].Chinese Annals of Mathematics, Series B,2016,37B(5):767.
- [2] TAO Z X. 2-Adjacency between pretzel links and the trivial link[J].Topology and its Applications,2016,214:186.
- [3] TAO Z X. 2-Adjacency between some special links and pretzel links[J].Journal of Knot Theory and its Ramifications,2018,27(12):1850062-1.
- [4] TORISU I. On 2-adjacency relation of two-bridge knots and links[J].Journal of the Australian Mathematical Society,2008,84(1):139.
- [5] TORISU I. On 2-adjacency relation of links[C]//Proceedings of the International Workshop on Knot Theory for Scientific Objects. Osaka:Osaka Municipal Universities Press,2007:277.
- [6] KAUFFMAN L H. On knots[M].Princeton:Princeton University Press,1987.
- [7] KAWAUCHI A. A survey of knot theory[M].Berlin:Birkhäuser,1996.
- [8] LICKORISH W B R, MILLETT K C. A polynomial invariant of oriented links[J].Topology,1987,26(1):107.
- [9] HOSTE J. The first coefficient of the Conway polynomial[J].Proceedings of the American Mathematical Society,1985,95(2):299.
- [10] MASBAUM G, VAITROBW A. A new matrix tree theorem[EB/OL].(2002-02-28)[2021-11-25].https://arxiv.org/abs/math/0109104v2.
- [11] LICKORISH W B R, MILLETT K C. Some evaluations of link polynomials[J].Commentarii Mathematici Helvetici,1986,61:349.
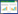 图 1 L4a1和L9n10
Fig.1 L4a1 and L9n10
图 1 L4a1和L9n10
Fig.1 L4a1 and L9n10