目前大量的互联网公开课程和智能学习指导平台,为学生随时随地可以相对独立地学习课程和完成相关练习提供了方便。追踪学生的知识点掌握情况,对学生的知识水平状态进行评定是一个相当重要的工作。知识追踪(knowledge tracing,KT)是根据学生以往的答题记录对其现阶段的知识掌握情况来进行建模。早期的知识追踪方法主要基于机器学习的模型,其中贝叶斯知识追踪(Bayesian knowledge tracing,BKT)[1]是构建学生知识状态的经典模型。BKT模型把学生的隐藏知识状态设成一个二元变量,利用隐马尔科夫模型(hidden markov model,HMM)更新每个二元变量取值的概率,但BKT模型高度依赖专家对知识点和练习题的标注,其实际应用范围受限。循环神经网络(recurrent neural network,RNN)可以摆脱对人工标注的依赖,且对高维向量有更好的表达效果,而应用到具体模型中的是其改进算法,即长短期记忆网络(long-short-term memory network,LSTM)[2]和门控循环神经网络(gated recurrent unit network,GRU)[3]。Piech等[4]提出的基于LSTM的深度知识追踪(deep knowledge tracing,DKT)是最早的深度学习模型。针对DKT模型序列容量过小的不足,后来的研究者做了一系列的改进[5-6]。另一改进算法GRU结构LSTM的优化版,其参数量更少,运行时间更短,能在保证LSTM神经网络预测效果的前提下做到模型结构更简洁,它在知识追踪领域同样也有应用。李浩君等[7]将学习交互序列输入双向的GRU神经网络中,预测结果良好。然而,刘铁园等[8]认为基于RNN的知识追踪模型仅提高了序列的学习容量,并没有解决RNN存在长期依赖的问题,即当前系统的状态可能受很长时间之前系统状态的影响。此外,动态键值记忆网络(dynamic key value memory networks[9],DKVMN)则从解释性视角对知识追踪模型进行改进,它利用一个静态矩阵来储存概念,以及一个动态矩阵来存储和更新对应概念的掌握情况; 与DKT相比,DKVMN有着更好的解释性。近年来,基于注意力机制[10]的模型开始在知识追踪领域占据主导地位,它能解决DKT模型的长期依赖问题。Pandy等[11]首先将注意力机制引入知识追踪的模型,提出了自注意力知识追踪(self-attention knowledge tracing,SAKT),该模型首先识别学生以往练习之间的交互性,然后预测学生在今后特定练习中的表现; 在多个公开数据集上与基准模型相比,平均曲线下方面积(area under curve,AUC)值小幅提升。Choi等[12]针对SAKT注意力层太浅和注意力权重不合理等问题,提出了可分离自注意力知识追踪(separated self-attention neural knowledge tracing,SAINT)模型,在私有数据集上,AUC值略微提升。Ouyang等[13]受遗忘机制研究的启发,在注意力机制中引入指数衰减项,提出了位置感知自注意力知识追踪(position-aware self-attentive KT,PAKT)模型,AUC值与SAKT模型相比提升明显。
以上基于注意力机制的知识追踪模型都是以注意力为基本架构,虽加深了网络结构,但未考虑与其他网络结构的融合,因而获取的序列特征比较单一。因此,本研究针对现有的基于注意力机制的知识追踪模型中存在序列信息提取不足、结构编码单一等问题,提出了一种改进的知识追踪模型。
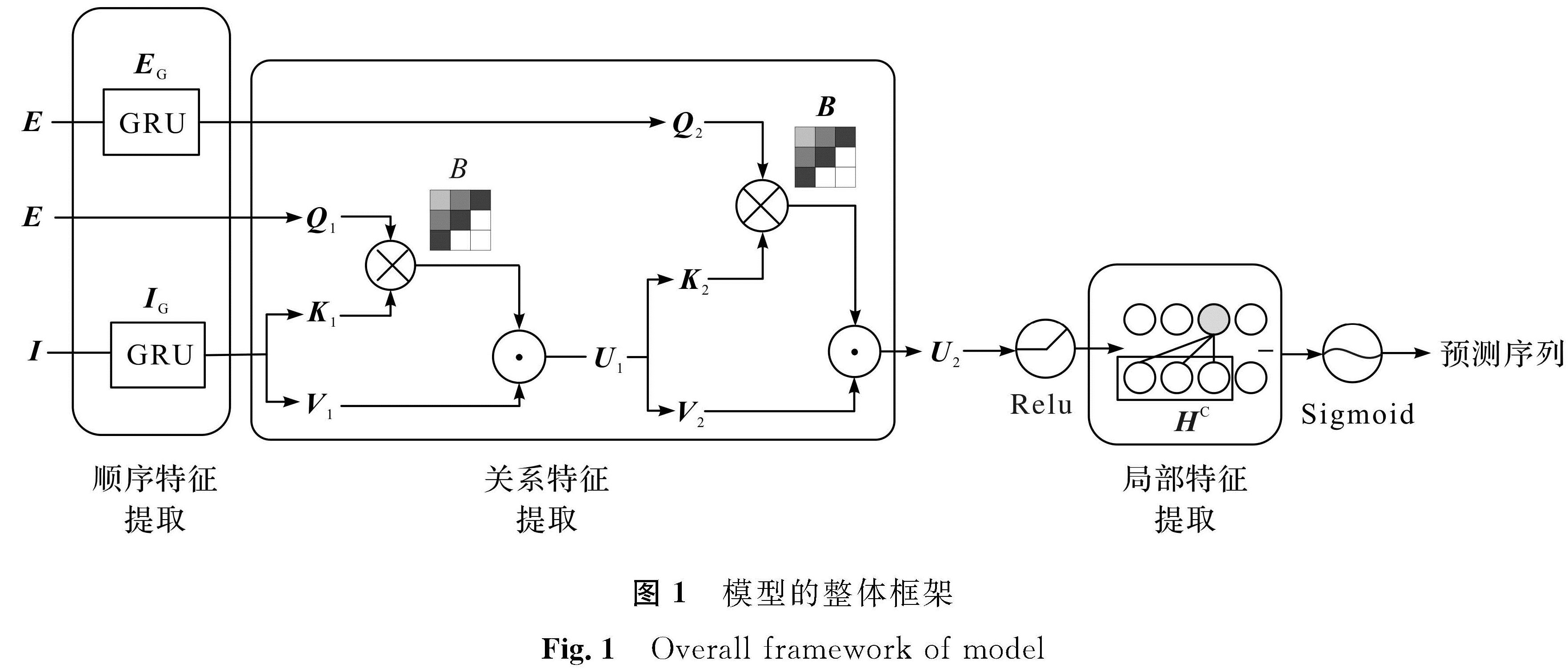
1 本文模型介绍1.1 模型架构本文模型的整体框架如图1所示,其中利用GRU提取序列的顺序特征,用注意力机制提取序列的关系特征,用因果卷积提取序列的局部特征。模型有3个输入:经过编码的2个练习序列E和反应序列I。首先将E作为Q和经过GRU神经网络的IG作为K、V输入带有位置缩放的注意力模块中; 然后把注意力的输出作为K、V和经过GRU神经网络的EG作为Q输入下一个带有位置缩放的注意力机制中,得到学生学习的序列向量U2,再经过因果卷积后得到向量HC,HC最后通过Sigmoid函数得到预测序列。
1.1.1 输入层与嵌入层
在输入序列的向量表示中采用独热编码(one-hot encoding),这与DKT、SAKT模型中的表示方法相同。例如,在一个数据集中,涉及M个知识点,所有的题目都属于这M个知识点,每道题的选择有两种,即{对,错}。对于第i个知识点的某道题,当回答正确时,向量的第M+i个位置为1,其余位置为0; 反之,当回答错误时,向量的第i个位置为1,其余位置为0,向量的总长度为2M,模型只关注题目所属的知识点和做题的结果。经过独热编码处理后,练习序列的维数变成了M维,反应序列的维数变成了2M维。为了满足模型的输入要求,本研究把序列的最大长度固定为n。
嵌入(embedding)主要应用于自然语言处理任务中,它把编码后的语言或文字转换成固定长度的向量。嵌入层将经独热编码后的练习序列和反应序列维数转换成隐藏层维数d,并适用于下一层网络的输入。简言之,嵌入过程就是一个矩阵乘法过程。经嵌入后的反应序列I∈Rn×d,练习序列E∈Rn×d。
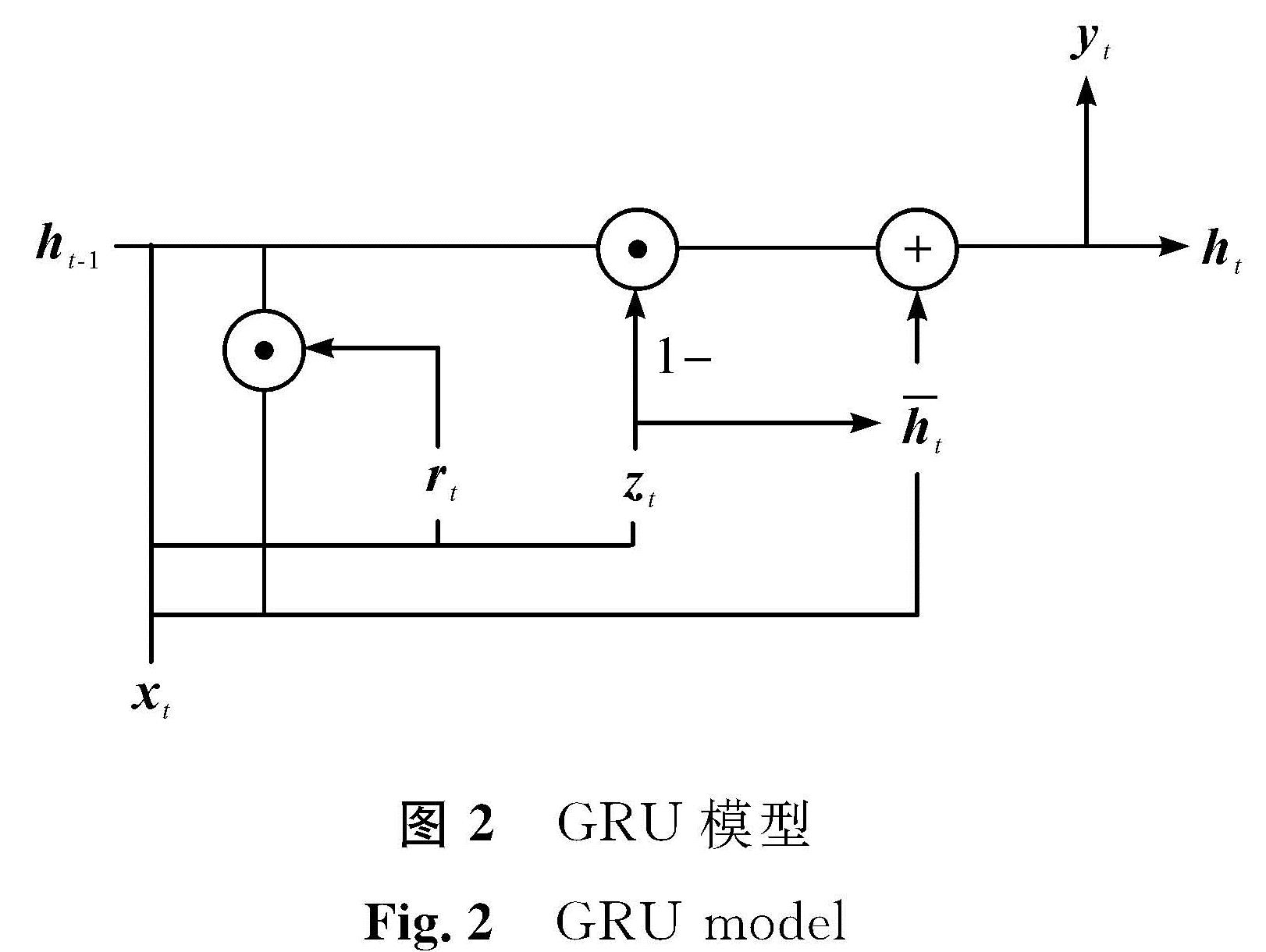
1.1.2 GRU层GRU层旨在学习学生的学习状态与不同练习隐藏表征。在GRU层中,隐藏层的数量和嵌入的向量维数相同。GRU结构输入包括当前的xt和上一个节点传递下来的隐藏状态ht-1,输出包括输入下一个节点的隐藏状态ht和当前的输出yt,rt和zt分别为控制重置和更新各门控单元,h^-t包含了当前输入xt的大部分信息,而ht选择性地保留上一层ht-1和当前xt信息的更新隐藏层。具体的计算过程如下:
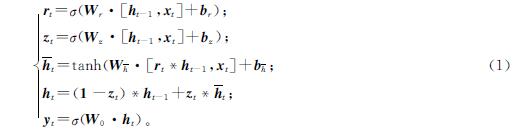
式(1)中:“σ”表示Sigmoid函数; “*”表示数组元素依次相乘; “·”表示矩阵乘法; Wr、Wz、Wh^-和W0为模型参数; br、bz和bh^-为模型偏置量。经GRU层得到的序列IG、EG的维度不变,直接输入下一层网络结构。GRU模型如图2所示。
1.1.3 注意力层
学生所做练习之间的关系对其掌握的知识状态有影响,采用PAKT中的权重指数衰减机制捕捉这种影响。第一个注意力计算查询矩阵和键值对公式如下:
Q1=EWq1; K1=IGWk1; V1=IGWv1 (2)
式(2)中:Wq1、Wk1和Wv1均为参数矩阵,用来学习之前做的练习题对现在练习题的影响。此外,引入一个指数衰减项,在较短的距离内可以获得更高的权重。注意力权重的计算公式如下:
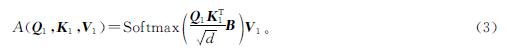
对B,在相应每个项上乘以一个指数项β i-j,其中,i≥j,β<1。Softmax项具体计算如下:

上述针对的是一个注意力矩阵,为了从数据中获得更充分的信息,本研究使用多个注意力矩阵,即多头注意力机制:

式(5)中: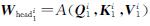 ; c为矩阵拼接操作; 参数矩阵
; c为矩阵拼接操作; 参数矩阵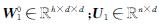 。
。
为了更好地捕捉学生过去所做练习对现在的影响,本研究把EG作为Q输入注意力机制中。第2个注意力计算查询矩阵和键值对公式如下:
Q2=EGWq2; K2=U1Wk2; V2=U1Wv2 (6)
式(6)中:Wq2、Wk2和Wv2均为参数矩阵。注意力权重计算公式如下:
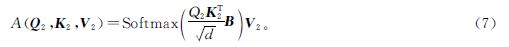
多头注意力计算公式如下:

式(8)中: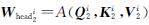 ; 参数矩阵
; 参数矩阵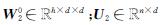 。经过注意力机制处理的U2此时包含学生对知识概念的掌握情况,接着它将会被输入网络结构下一层。
。经过注意力机制处理的U2此时包含学生对知识概念的掌握情况,接着它将会被输入网络结构下一层。
本研究用因果卷积进行局部特征提取。因果卷积每层的输出都是由前一层未知的输入和前一层相同位置的输入共同得到的,它通过控制卷积核的大小来实现局部特征的提取,解决了传统卷积不能解决的序列问题。卷积核的大小固定在一个具体范围内,只有在这个范围内的序列才会被计算,而传统卷积里的一个输出是由卷积核对应的感受野计算出来的。这种计算方式考虑了序列的顺序性,与目标序列的要求一致。
将学生知识点掌握特征U2∈Rn×d作为该层的输入。具体地,输入UT2=(m1,m2,…,mn),mi∈Rd×1,通过卷积获得HC=(hC1,hC2,…,hCn+k-1)∈Rd×(n+k-1),其中:
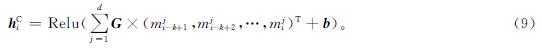
式(9)中:G∈Rd×k,即d个长度为k的卷积核; mji为mi的第j维元素; b∈Rd×1为函数偏置项; Relu=max(0,x)为激活函数。为了便于模型的运行,本研究取前n维,即这一层的输出为HC∈Rd×n。
1.1.5 预测层将经过因果卷积后的HC输入一个激活层,通过这个激活层来预测学生的表现,具体公式如下:
pi=Sigmoid((HC)TW0) (10)
式(10)中:pi为学生在某一具体问题做出正确答案的概率; W0∈Rd×N,N为题目总数; Sigmoid(Z)=1/(1+e-z)。
1.2 模型优化目标模型训练目的是获得学生反应序列的负对数可能性的最小值,参数的更新是通过最小化预测值pi和实际值ri之间的交叉熵来实现的,该优化目标与文献[13]288一致,具体公式如下:
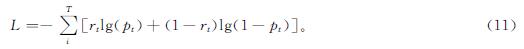
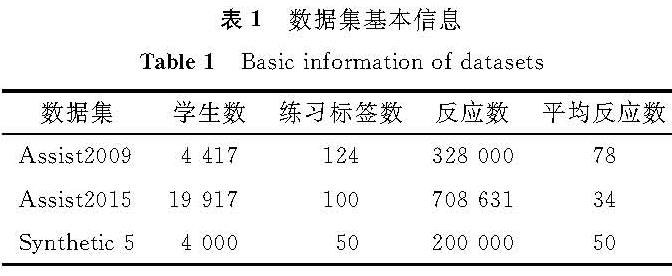
为了检验模型的可行性与有效性,本研究采用3个公开的数据集,其基本信息见表1。
Assistment2009(Assist2009)[14]由Assistment网上指导平台提供,广泛应用于知识追踪任务。本研究在“skill-builder”数据集上测试本文模型。Assistment2015(Assist2015)[15]包含了学生在100个技能上作答情况,表1中为反应数,总的反应数是708 631个,一共有学生19 917人,它比Assist2009数据集的数据量大,但其每个学生的平均反应数比Assist2009少。Synthetic-5[4]24是通过模拟4 000个虚拟学生的做题记录得到,其中每个学生回答同样顺序的50个练习,这些练习从5个不同难度层次的虚拟概念中提取出来。
本研究采用的深度学习框架为Pytorch。经过多次试验,模型参数设置如下:序列长度固定为50,隐藏层数量d=128,CNN卷积核大小为7,缩放比例β为0.6。本研究使用Adam优化器训练本文模型,其中参数lr=0.001,β1=0.9,β2=0.999,ε2=0.999,-8。为了保证训练的有效性及模型之间的可对比性,本研究数据集划分比例与PAKT模型一致。Assist2009和Assist2015数据集按照13:3:4的比例来划分训练集、验证集、测试集; 与前面2个数据集不同,Synthetic-5按照8:2的比例来划分训练集和测试集,没有验证集。
本研究选择AUC值作为衡量模型优劣的指标。在知识追踪领域,AUC值是一个通用指标。AUC指接受者操作特性曲线(receiver operating characteristic curve,ROC)下方的面积,使用AUC值作为模型的评价指标是因为ROC曲线虽不能清晰地说明哪个分类器的效果更好,但是通过比较AUC值大小可以判断模型好坏,值越大效果越好。
2.2 试验分析2.2.1 模型结构的选取研究为探究本文模型的有效性,对模型各部分的选取进行探究。
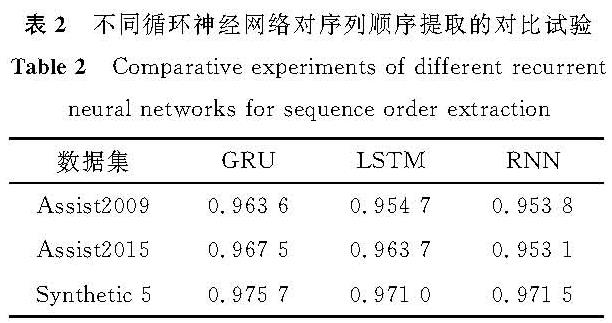
表2为不同循环神经网络对序列顺序提取的对比试验,分别引入RNN和LSTM与GRU。GRU和LSTM与RNN相比,引入门限结构,避免了梯度消失问题; 而GRU与LSTM相比,参数量更小,不易过拟合。从试验结果看,GRU在3个数据集上的AUC值均最大,GRU提取序列的顺序特征最有效,因此,本研究选择GRU作为本文模型的一部分。
表3为不同注意力机制的掩码对比试验。在本文模型中,选取带有指数递减的掩码,即PAKT中的注意力机制,并引入原先SAKT中的掩码进行对比。从试验结果看,PAKT中的注意力机制在数据集Assist2009和Assist2015上表现最佳,在Synthetic-5上SAKT效果最好,因此选择在2个数据集上表现均较好的PAKT中的注意力机制,作为本文模型的注意力机制。
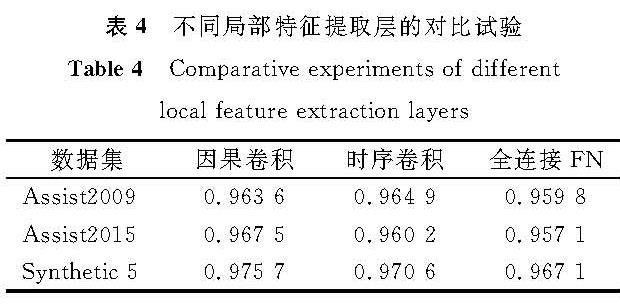
表4为PAKT中不同局部特征提取层的对比试验。SAKT模型使用全连接层,PAKT使用因果卷积,本文模型也使用因果卷积,但因果卷积获取的特征有限,对比试验引入时序卷积(temporal convolutional network,TCN)[16],它能捕获比因果卷积更长距离的信息,并且存在稳定的梯度。从试验结果看,时序卷积在多数数据集上的表现不如因果卷积,即时序卷积中的灵活感受野并没有发挥很好的效用,这说明在经过2层注意力层后,数据顺序上的特征已经提取出来了,使用因果卷积已经足够。因此,选择因果卷积作为本文模型的一部分。
表2 不同循环神经网络对序列顺序提取的对比试验
Table 2 Comparative experiments of different recurrent neural networks for sequence order extraction
2.2.2 与基准模型的对比试验
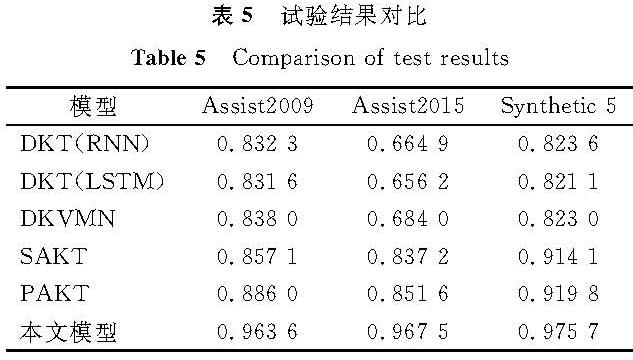
将本文模型与前文介绍的DKT、DKVMN、SAKT、PAKT等基准模型进行对比,试验结果见表5。训练对比方法时,超参数的使用和文献[13]相同。DKT(RNN)、DKT(LSTM)均使用一层循环神经网络,隐藏层数量为200。在DKTVM中,记忆(memory)值设置为20。在SAKT、PAKT中,头数值设置为8,隐藏层数量设置为128。由表5可知,在3个数据集上,本文模型与基准模型相比,AUC值都有大幅提升,效果优异。在Assist2009、Assist2015和Synthetic-5上,与PAKT模型相比,本文模型AUC分别提升了0.077 6、0.115 9和0.055 9,平均提升了0.083。当本文模型第2次把练习序列作为Q输入注意力机制中时,相当于把学过的知识点再学一遍,学生在各知识点上的掌握情况分布相比其他模型更合理; 此外,加入的GRU网络能捕捉到习题之间的关系及学生历史做题信息之间的关系,因果卷积能把不同大小的局部信息都考虑进去。这些因素能使本文模型比其他模型的表现更优秀。
2.2.3 超参数试验研究
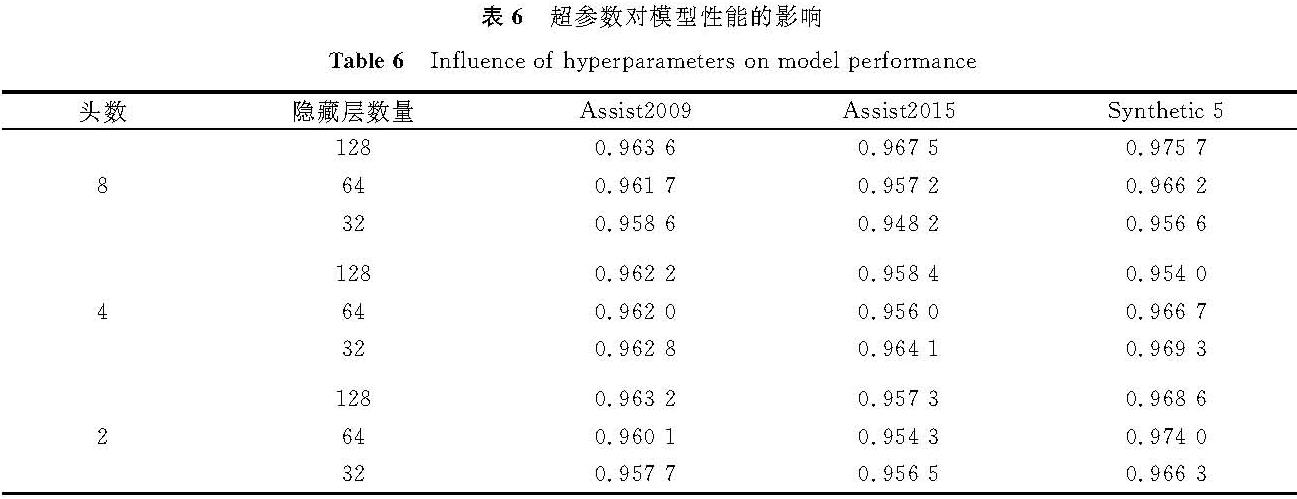
为了研究超参数对模型的影响,本研究设计了如下试验。将GRU神经网络中的隐藏层数分别取128、64、32,注意力机制中的头数分别设置为8、4、2。超参数对模型性能的影响见表6。由表6可知,不同超参数设置的模型性能略有差别。所以,在模型训练效率相差不大的情况下,本研究选择更多的隐藏层数和头数作为本文模型的超参数,即头数为8,隐藏层数为128。
2.2.4 模型可视化分析
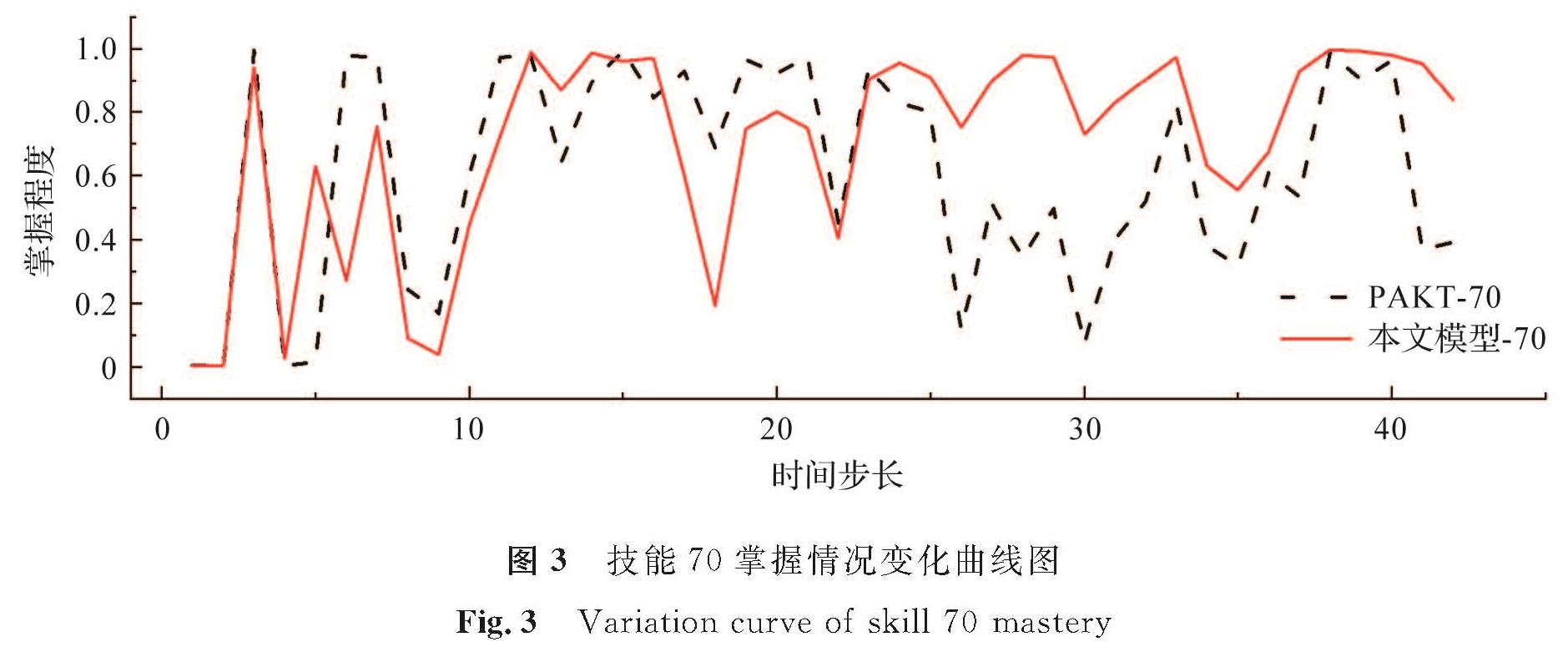
为了更直观地展示试验结果,在模型参数训练完成后,选取某一学习记录输入模型中,记录模型激活函数最后的输出值,用该输出值代表学生在知识点上的掌握程度。本研究选取Assist2009数据中某个学生的学习记录,作了技能70学习状态变化的曲线图,并与经PAKT模型预测的曲线进行比较。技能70掌握情况变化曲线如图3所示。从整体来看,本文模型-70的方差比PAKT-70的方差更小,即曲线整体更平稳; 从局部来看,在前20的时间步长上,两个模型走势几乎一样,但在后部分,本文模型-70的预测值明显在高位,波动性也比PAKT-70要小。这说明再学一遍的学生的学习掌握状态比只学了一遍的学生要好,这也再次说明了本文模型的有效性。
3 结 语
本研究提出了融合多种结构的深度知识追踪新模型,能较好地捕捉知识追踪模型特征,并且针对注意力机制中Q、K、V的选择做了进一步的探索。与最初的基于注意力机制的模型相比,本文模型的深度加深,序列的输入更宽,模型结构更丰富; 除此之外,本文模型还在注意力的基础上加上了GRU,使得输入序列的顺序特征能被捕捉,且在输入注意力层之后效果得到了明显提升。本文模型在多个数据集上表现良好,能更好地预测未来学生的表现。
知识追踪问题可以归类为单向序列问题,在其他领域的应用模型也可用到知识追踪模型中。针对带有注意力机制的知识追踪模型,未来要继续降低模型的复杂度; 此外,还可加入更多的特征,例如技能点之间的拓扑结构,学习者练习的时间因素,以更符合学生的实际状态。
- [1] YUDELSON M V, KOEDINGER K R, GORDON G J. Individualized bayesian knowledge tracing models[C]//Proceedings of the 16th International Conference on Artificial Intelligence in Education. Berlin:Springer,2013:171.
- [2] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J].Neural Computation,1997,9(8):1735.
- [3] KYUNGHYUN C, BART V M, CAGLAR G, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[C]//Empirical Methods in Natural Language Processing. Doha:Association for Computational Linguistics,2014:1724.
- [4] PIECH C, SPENCER J, HUANG J, et al. Deep knowledge tracing[J].Computer Science,2015,3(3):19.
- [5] ABDELRAHMAN G, WANG Q. Knowledge tracing with sequential key-value memory networks[C]//Proceedings of the 42nd Int Conference on Research and Development in Information Retrieval(SIGIR). New York:ACM,2019:175.
- [6] SHA L, HONG P Y. Neural knowledge tracing[C]//Proceedings of the International Conference on Brain Function Assessment in Learning. Berlin:Springer,2017:108.
- [7] 李浩君,方璇,戴海容.基于自注意力机制和双向GRU神经网络的深度知识追踪优化模型[J].计算机应用研究,2022,39(3):732.
- [8] 刘铁园,陈威,常亮,等.基于深度学习的知识追踪研究进展[J].计算机研究与发展,2022,59(1):81.
- [9] ZHANG J N, SHI X J, KING I, et al. Dynamic key-value memory networks for knowledge tracing[C]//Proceedings of the 26th International Conference on World Wide Web. New York:ACM,2017:765.
- [10] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Proceedings of Advanceson Neural Information Processing Systems. Long Beach:Curran Associates Inc,2017:5998.
- [11] PANDEY S, KARYPIS G. A self-attentive model for knowledgetracing[EB/OL].(2019-07-16)[2022-07-18].
- [12] CHOI Y, LEE Y, CHO J, et al. Towards an appropriate query, key, and value computation for knowledge tracing[C]//Proceedings of the Seventh ACM Conference on Learning Scale. New York:Association for Computing Machinery,2020:341.
- [13] OUYANG Y X, ZHOU Y C, ZHANG H B, et al. PAKT:a position-aware self-attentive approach for knowledge tracing[C]//Pro-ceedings of International Conference on Artificial Intelligence in Education. Cham:Springer,2021:285.
- [14] FENG M, HEFFERNAN N, KOEDINGER K. Addressing the assessment challenge with an online system that tutors as it assesses[J].User Modeling and User Adapted Interaction,2009(19):243.
- [15] XIONG X L, ZHAO S Y, VAN I, et al. Going deeper with deep knowledge tracing[C]//Proceedings of the 9th International Conference on Educational Data Mining. Raleigh:IEDMS,2016:545.
- [16] BAI S, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequencemodeling[EB/OL].(2018-04-19)[2022-07-18].
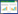 图 1 模型的整体框架
Fig.1 Overall framework of model
图 1 模型的整体框架
Fig.1 Overall framework of model