k-WTA(k-winners-take-all,k-赢者通吃)网络是一种能从一组输入数据中选择前k个最大值的竞争型神经网络。赢者通吃(winner-take-all,WTA)网络[1]作为k-WTA网络的一种特例,在图像分类[2]、模式识别[3]、神经网络电路[4]等领域得到了广泛的应用。在智能计算领域中,这类从输入数据中取最大值的操作是极其重要的。因此,国内外研究者对k-WTA网络开展了一系列研究,如Majani等[5]首次提出并研究了WTA网络的泛化形式k-WTA网络,保证了模型的局部稳定性。Calvert等[6]提出了模拟浩斯菲尔德神经网络,并通过完整的数学分析证明了它可以有效地识别实数列表中的前k个最大分量。
为了优化模型结构,Liu等[7]首次将k-WTA问题转换为一个等价的二次规划问题。进而动态神经网络、对偶神经网络、投影神经网络等陆续被开发应用[8],同时在引入激活函数[9]、收敛速度[10]等方面进行了改进。这些模型在处理常数输入的k-WTA运算时能实现有限时间收敛,但在处理时变输入信息时存在滞后误差,需通过设置足够大的参数来改善。Peng等[11]设计了具有非硬限制激活函数的k-WTA神经网络,极大地简化了模型结构,降低了计算成本。Qi等[12]设计并研究了利用饱和允许激活函数执行k-WTA操作的k-WTA神经网络,该网络具有较强的扰动鲁棒性。Liu等[13]设计并分析了具有较高精度和较强鲁棒性的k-WTA网络,并给出了多机器人系统中执行跟踪任务的应用,验证了该网络的有效性。
近年来,机器人技术在工程领域得到了迅速的发展,受到了广泛的关注,并取得了丰硕的成果。单个机器人虽然在很多方面满足了一些行业的需求,但在一些复杂或大规模作业中经济效益不高。针对这一不足,出现了多机器人系统,其明显的优点是能够通过机器人的协同,高效、灵活地完成任务。现有的多机器人系统大多采用集中式控制方法,依赖一个控制中心,除了存在潜在的不稳定因素外,还存在计算量大、通信负荷高的问题。与集中式方法相比,分布式方法只需要邻居对邻居的通信,大幅减轻了整体通信负荷,即使某些机器人失效,分布式方法仍能正常工作。到目前为止,对k-WTA的研究大多使用集中式控制方法,即没有加入任何拓扑约束,不能被直接用于具有任意拓扑结构的多智能体网络。Li等[14]首次考虑了多智能体网络的拓扑结构,提出了一种分布式WTA模型来解决网络中的动态竞争问题。Jin等[15-16]研究了基于k-WTA的多机器人分布式竞争协同,并采用了低通一致性滤波器来估计k-WTA模型中的动态项,使得单个机器人能够仅依靠其邻居信息计算出对整个系统输出信息的均值估计。这些成果指出了研究分布式k-WTA网络的必要性,为后续基于k-WTA思路的广泛应用奠定了基础。
但据现有文献,关于分布式k-WTA模型的研究还很少。针对分布式k-WTA问题,本研究首先提出了一种使用高通一致性滤波器的分布式k-WTA模型。然后利用拉塞尔不变性原理(Lasalle's invariance principle)[17]计算出本模型有一个不变集,在不变集中本模型退化为现有的具有全局渐进收敛性的集中式k-WTA模型,证明了本模型全局渐进收敛于k-WTA问题的解。最后通过两个算例,验证了所提出的分布式k-WTA模型的性能。
1 k-WTA问题1.1 集中式k-WTA模型一般而言,k-WTA问题可以被表述为下列函数:
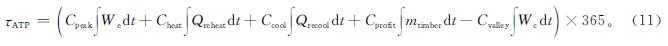
式(1)中:x∈Rs为输入向量; r∈Rs为输出向量; s为输入量和输出量的元素数。当ri=1时,第i个元素成为赢家; 否则,第i个元素就成了输家。上面的k-WTA问题也可以表示为如下的二次规划问题[18]:

式(2)中:η为设计参数; 0≤ri≤1,i=1,2,…,s; k为设定的赢家数量。当0≤2η≤(-overx)k-(-overx)k+1时,上述二次规划问题的解完全等价于式(1)中描述的k-WTA问题,其中(-overx)k表示x中的第k个最大元素。
为解决上述二次规划问题,一种单状态变量k-WTA网络模型被定义为

式(3)中:ζ为辅助变量; ε>0为设计参数; gi(·)为激活函数g(·)的第i个元素,其可被描述为

在式(3)中可以发现,无论问题规模大小,模型只有一个状态变量ζ。由于ζ总是需要输入向量x中所有元素的信息,所以k-WTA模型式(3)是集中式的。上述属性也出现在许多模型中,如简化对偶神经网络模型[7]1502,改进对偶神经网络模型[8]2023,具有阶跃激活函数的k-WTA网络模型[9]1498和单神经元的递归神经网络模型[10]1141。在下一章提出的分布式模型将基于k-WTA模型式(3),因为它是现有模型中最简单的。
1.2 分布式k-WTA问题受限通信拓扑可被定义为一个具有s个智能体的无向连接网络G(W,E,A),其中W表示点集,E表示边集,A表示邻接矩阵。设N(i)表示第i个智能体的邻居集,那么第i个智能体只能与邻居集N(i)中的对象交换信息。在这种情况下,k -WTA问题变成了如何借助智能体与邻居的竞争来在所有智能体中找到k个赢家。本研究的目的是寻找一种能够在受限通信条件下解决k -WTA问题的分布式模型。
2 分布式k-WTA模型2.1 模型描述在式(3)中,求和项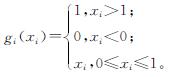 需要所有的智能体信息,是一个集中项。Zhang等[19]利用高通滤波器,将代数连通性估计模型中的集中求和项用局部信息计算出的估计值代替,得到相应的分布式模型。类似地,在式(3)的基础上,增加辅助状态向量p和q,利用高通一致性滤波器将求和项
需要所有的智能体信息,是一个集中项。Zhang等[19]利用高通滤波器,将代数连通性估计模型中的集中求和项用局部信息计算出的估计值代替,得到相应的分布式模型。类似地,在式(3)的基础上,增加辅助状态向量p和q,利用高通一致性滤波器将求和项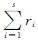 用估计值代替。结合受限网络的定义,构建如下分布式k -WTA模型:
用估计值代替。结合受限网络的定义,构建如下分布式k -WTA模型:
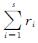
式(4)中:λ、δ、μ均为大于零的设计参数,其中0≤2μ≤(-overx)k-(-overx)k+1; aij为邻接矩阵A中第i行第j列的元素。
结合所有智能体的控制输入,分布式k -WTA模型式(4)可以写成如下形式:
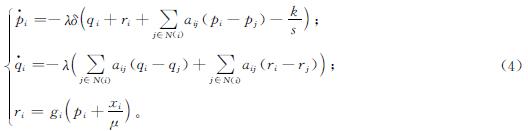
式(5)中:e为一个s维向量,所有元素都是1; L为通信图G的拉普拉斯矩阵,满足γ2min(L)≥7.5δ,γ2min(L)为L的第二个最小特征值。
2.2 理论分析定理1 假设q(0)=0,通信受限情况下的分布式k -WTA模型式(5)的输出值全局渐进收敛于k -WTA问题式(1)的解。
证明:定义函数h(p)=[h1(p1),h2(p2),…,hs(ps)]T,其元素hi(pi)定义如下:
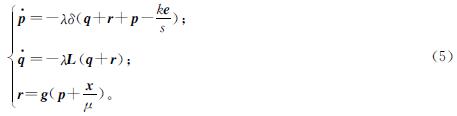
定义如下辅助变量:
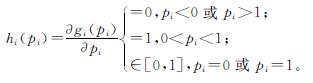
由式(5)我们可以得到:
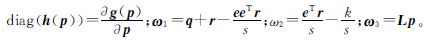
根据式(5)和式(6),ω2的导数如下:

式(7)中:‖·‖1为1-范数。同时得到ω1的导数如下:
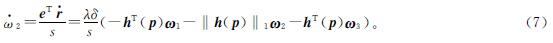
式(8)中:I为一个s维单位矩阵。对于一个无向连通图,拉普拉斯矩阵满足Le=eTL=0。利用拉普拉斯矩阵的性质,我们可以得到:
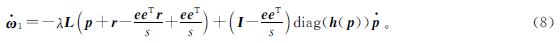
所以假设q(0)=0,我们可得eTω1≡0。根据以上性质,eTω1可以做出如下变化:
eTω1=(L+χeeT)ω1=Cω1。(10)
式(10)中:C=L+χeeT; χ≥γ2min(L)/s; 矩阵C满足γmin(C)=γ2min(L)>0,其中γmin(·)表示最小的特征值。因此,式(9)可以进一步写成:
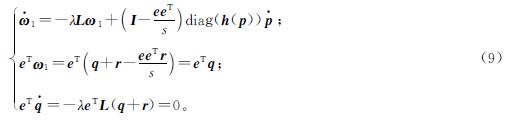
定义一个如下的李雅普诺夫函数:
V=V1+sV2+V3。(12)
式(12)中:V1=(ωT1ω1)/(2λ); V2=(ω22)/(2λ); V3=(pTLp)/(2λ)。
由V1、V2和V3的定义,很容易知道:
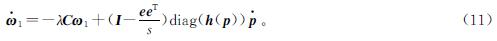
由于拉普拉斯矩阵L中的每一行元素之和都为0,所以V3=0。因此V为正定函数。计算V的时间导数,可以得到:
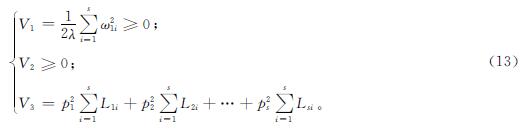

将式(6)与式(15)结合可得:
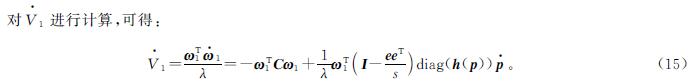
式(16)中:‖·‖2为2-范数; γmax(·)为最大特征值。根据2-范数的性质,由于h(p)为对角线,且其所有元素均不超过1,则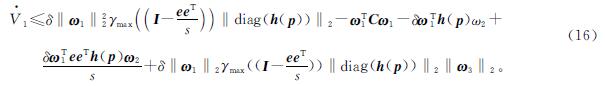 。此外,可以计算出γmax(I-eeT/s)=1。因此,可得:
。此外,可以计算出γmax(I-eeT/s)=1。因此,可得:
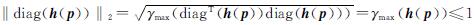
应用Cauchy-Schwarz不等式,可以得到:
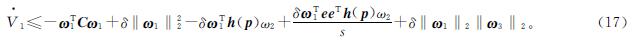
式(18)中:|·|为绝对值。对于不等式(16),可以进一步得到:
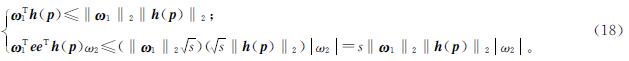
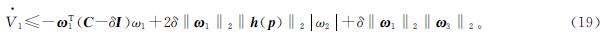
由于h(p)的每个元素都属于[0,1],所以‖h(p)‖1≥‖h(p)‖22。
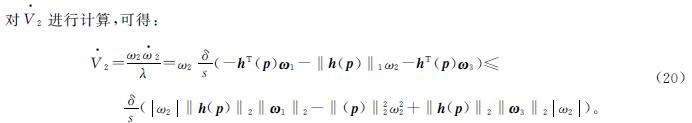
结合式(19)~(21)可得:
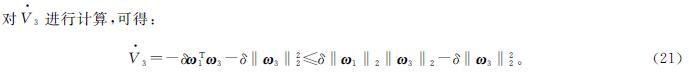
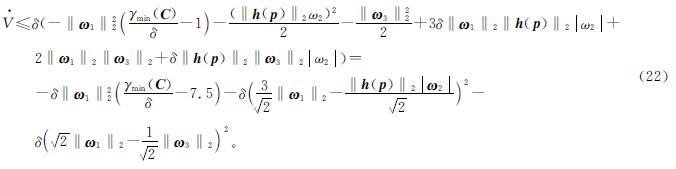
在式(23)两边同时左乘(eT/s)可得:

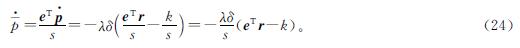
将式(24)和式(25)写为每个智能体的子公式,可以得到:
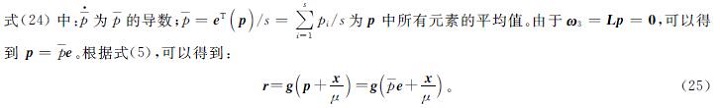
将式(25)中的参数用式(3)中的参数来替代,即令η=μ,ζ=(-overp),ε=λδ/s,可以发现式(25)完全等价于式(3),所以式(25)的输出值全局渐进收敛于k -WTA问题式(1)的解。因此,根据拉塞尔不变性原理,当q(0)=0时,通信受限情况下的分布式k -WTA模型式(5)的输出值全局渐进收敛于k -WTA问题式(1)的解。定理1成立。
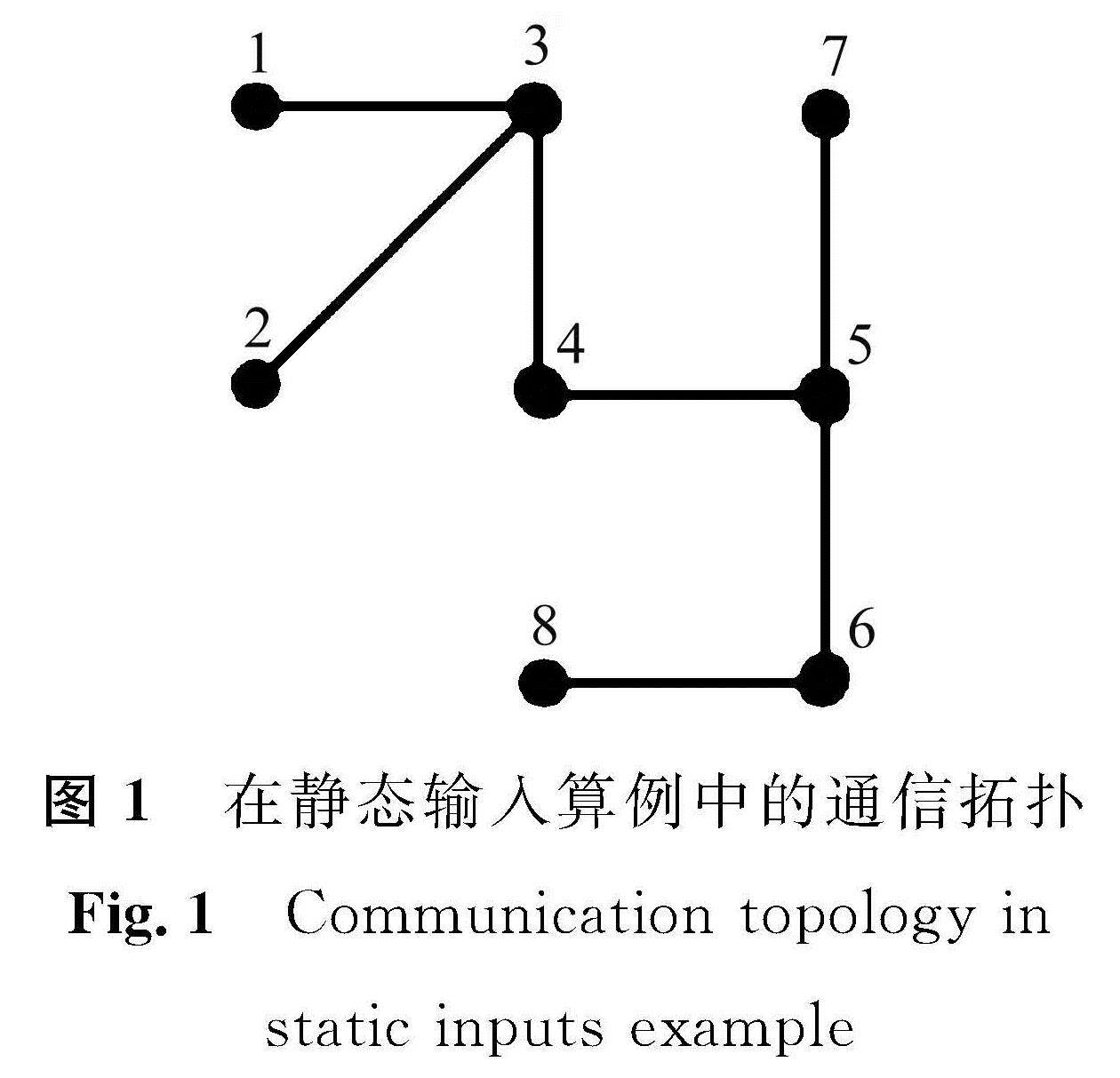
3 仿真验证3.1 静态输入算例在静态输入数值算例中,我们考虑使用分布式k -WTA模型在1个由10个智能体组成的受限通信网络中寻找2个赢家,即s=8,k=2。在静态输入算例中的通信拓扑如图1所示,其中每个节点代表1个智能体,节点间的连线代表这2个智能体之间可互相通信。为便于说明,暂不考虑通信的权重,即邻接矩阵A的元素满足aij∈{0,1}。
输入向量使用设定好的固定值,试验过程中赢家不会随时间t发生变化,将输入向量设置为
x=[6.5; 1.9; 2.9; 17.4; 14.8; 7.3; 20.0; 11.6]。
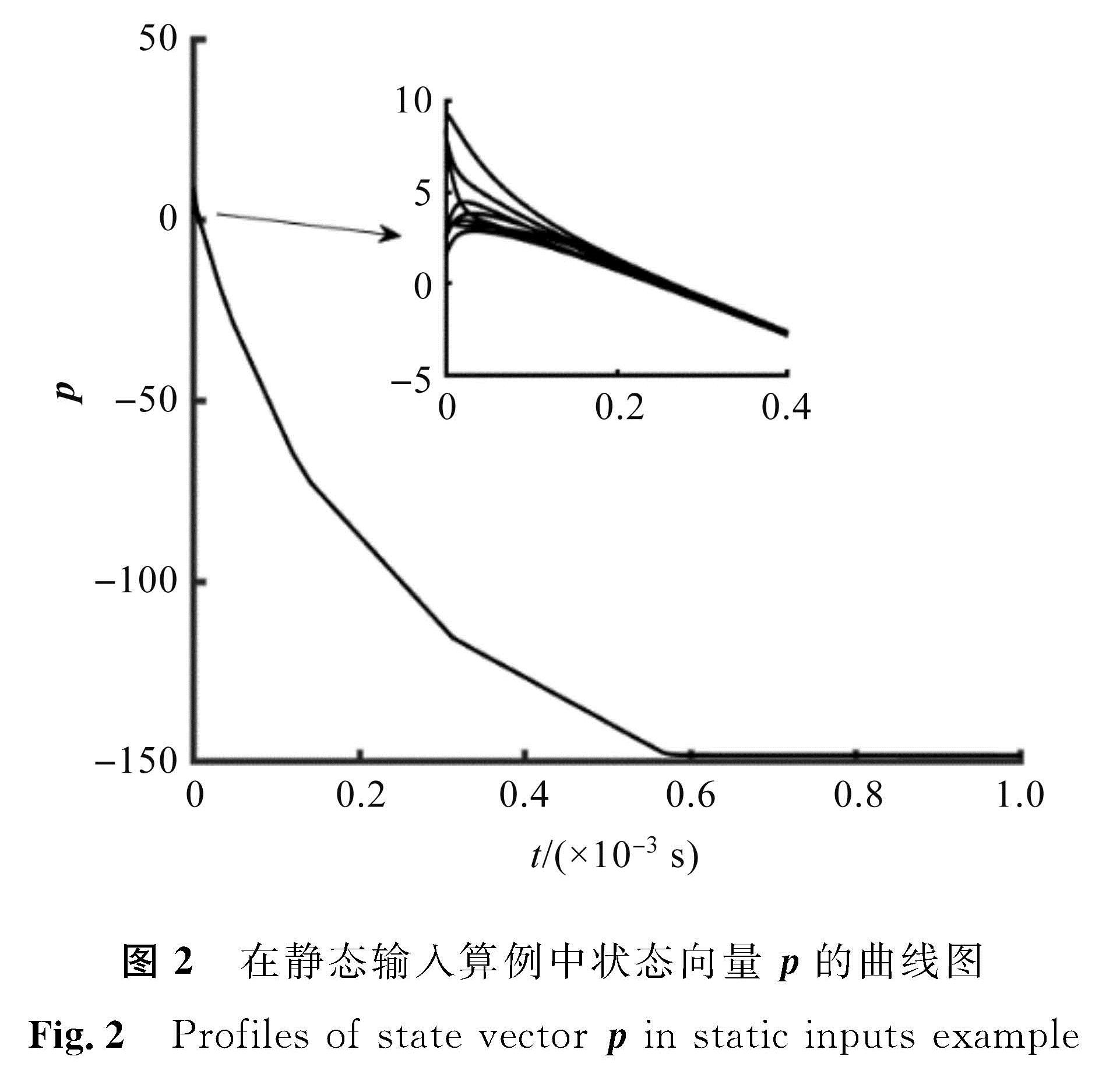
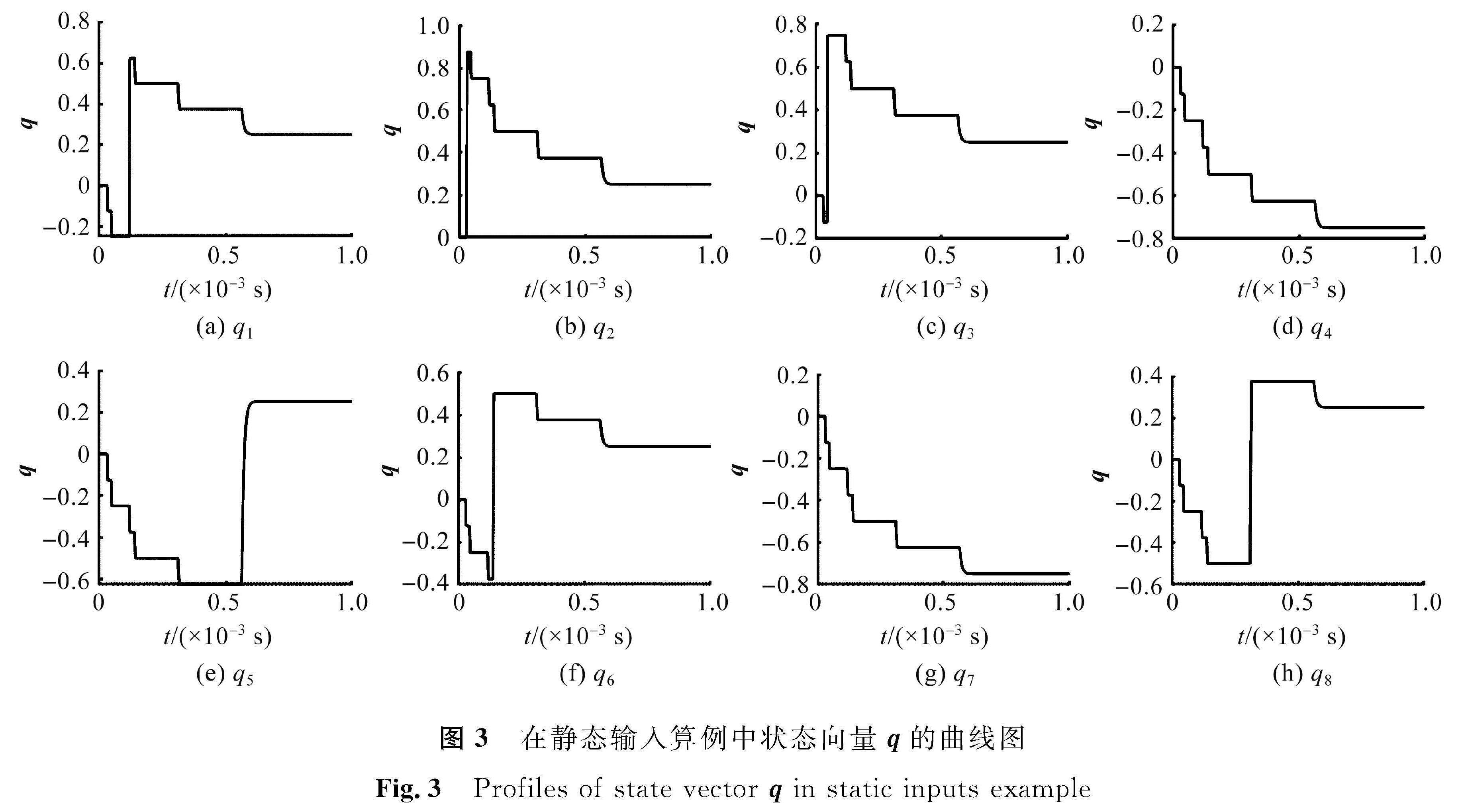
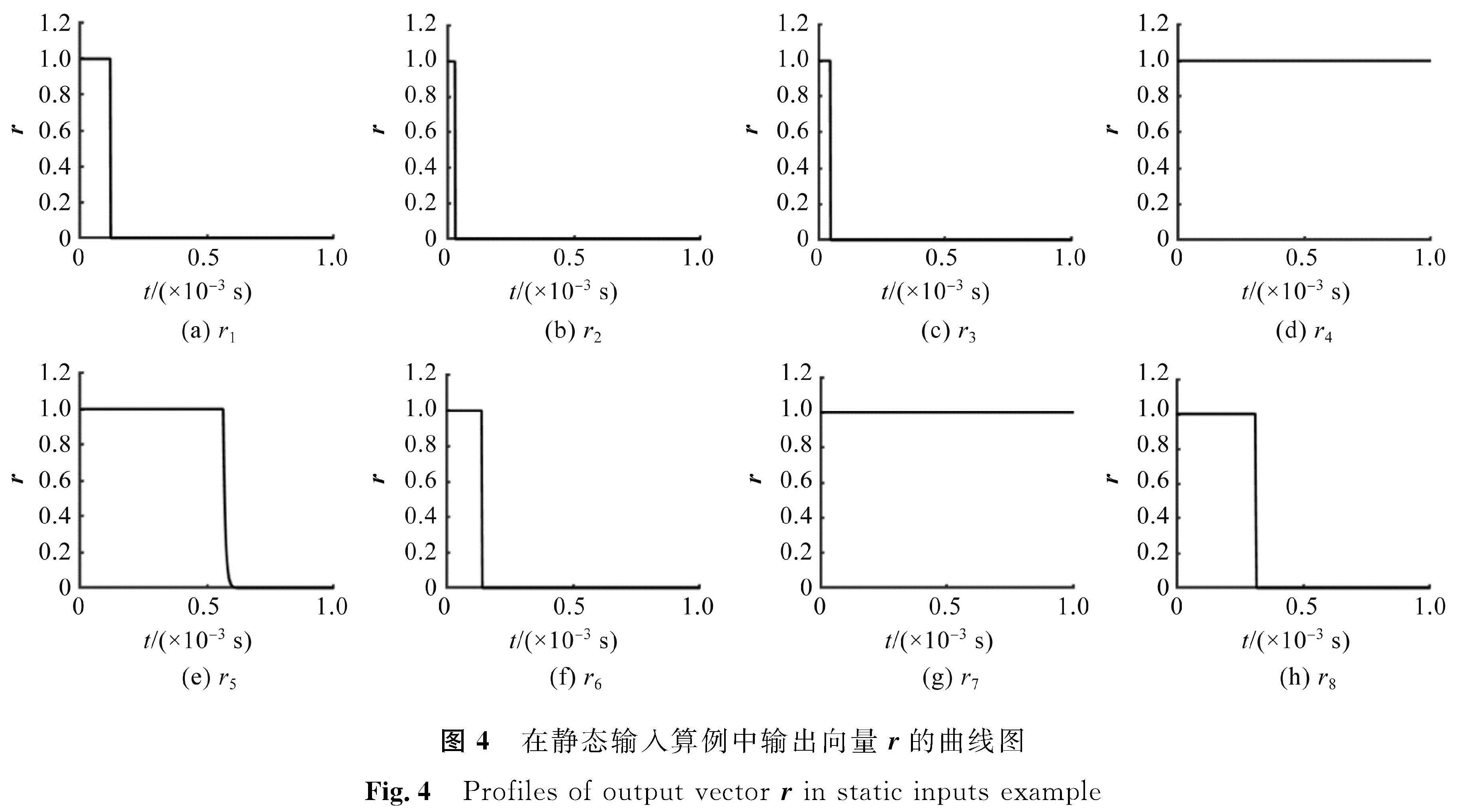
可以看出,第4、7个智能体将是赢家。相应的参数设定为λ=109,δ=0.001,μ=0.1。p的初始值是随机的,并且根据定理1将q的初始值设为0。在静态输入算例中状态向量p的曲线图见图2。在静态输入算例中状态向量q的曲线图见图3。在静态输入算例中输出向量r的曲线图见图4。可以看到所提出的分布式k -WTA模型在6×10-4 s内收敛于k -WTA问题的解。最终,输出向量中的第4、第7个元素均为1,其他元素均为0,表明所提出的分布式k -WTA问题的解。最终,输出向量中的第4、第7个元素均为1,其他元素均为0,表明所提出的分布式k -功选出了2个赢家。
3.2 动态输入算例
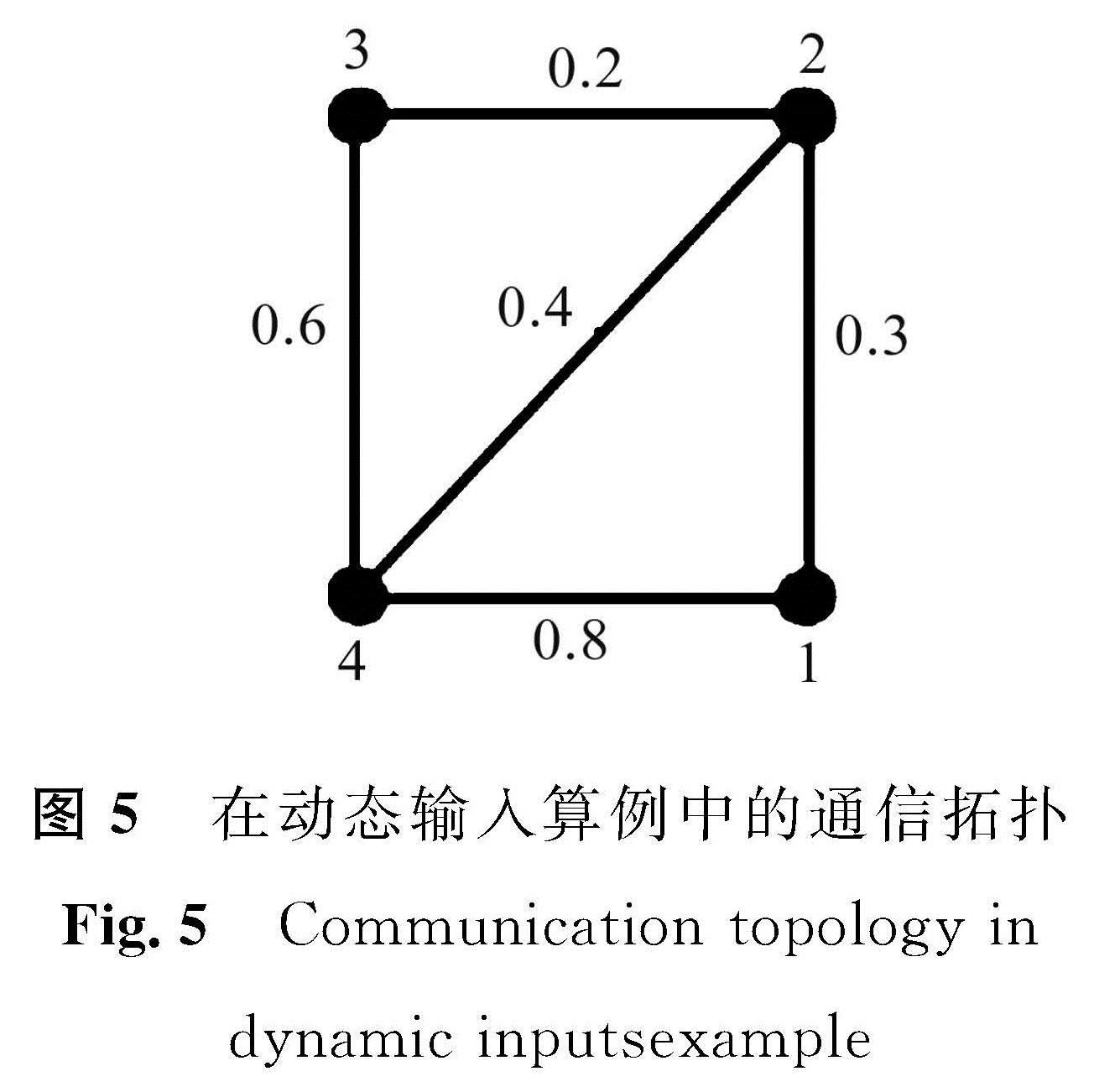
在动态输入数值算例中,我们考虑使用分布式k -WTA模型在由4个智能体组成的受限通信网络中寻找1个赢家,即s=4和k=1。在动态输入算例中的通信拓扑如图5所示,其中连线上的值代表通信权值。输入向量使用随时间变化的函数,在试验过程中赢家会随输入向量变化而改变,将其设置为
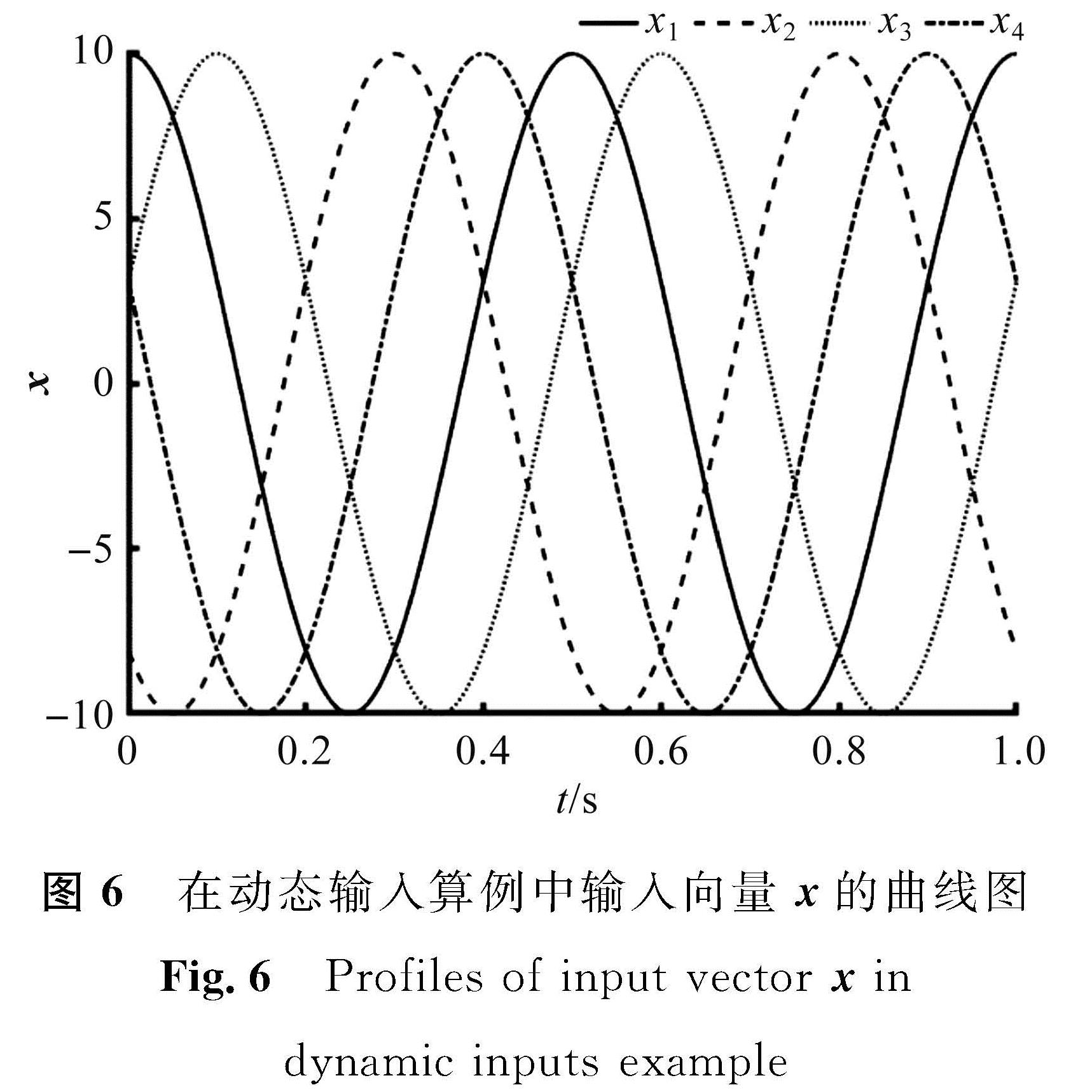
xi(t)=10cos(4π(t+0.2(i-1))),i=1,2,3,4。
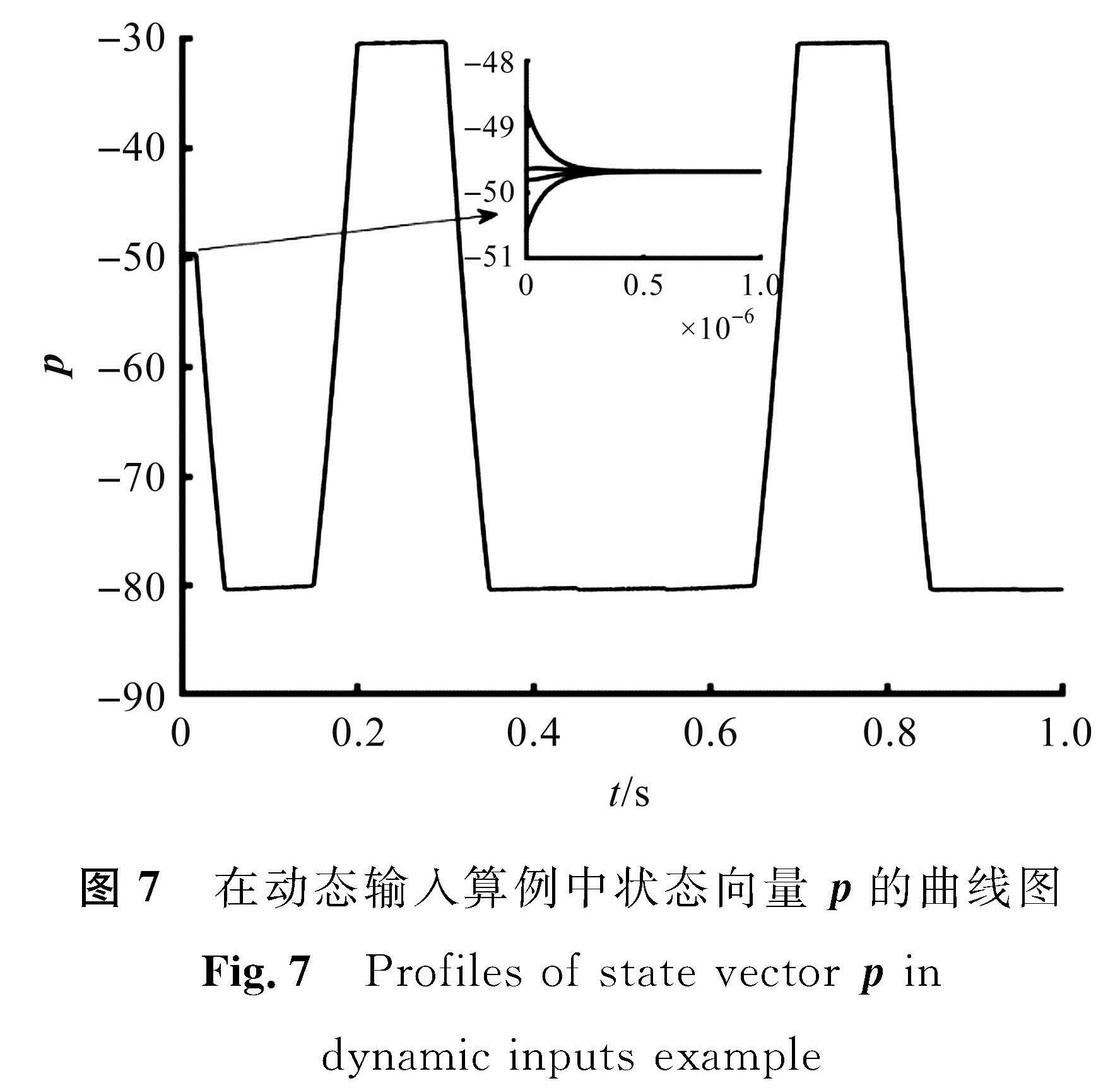
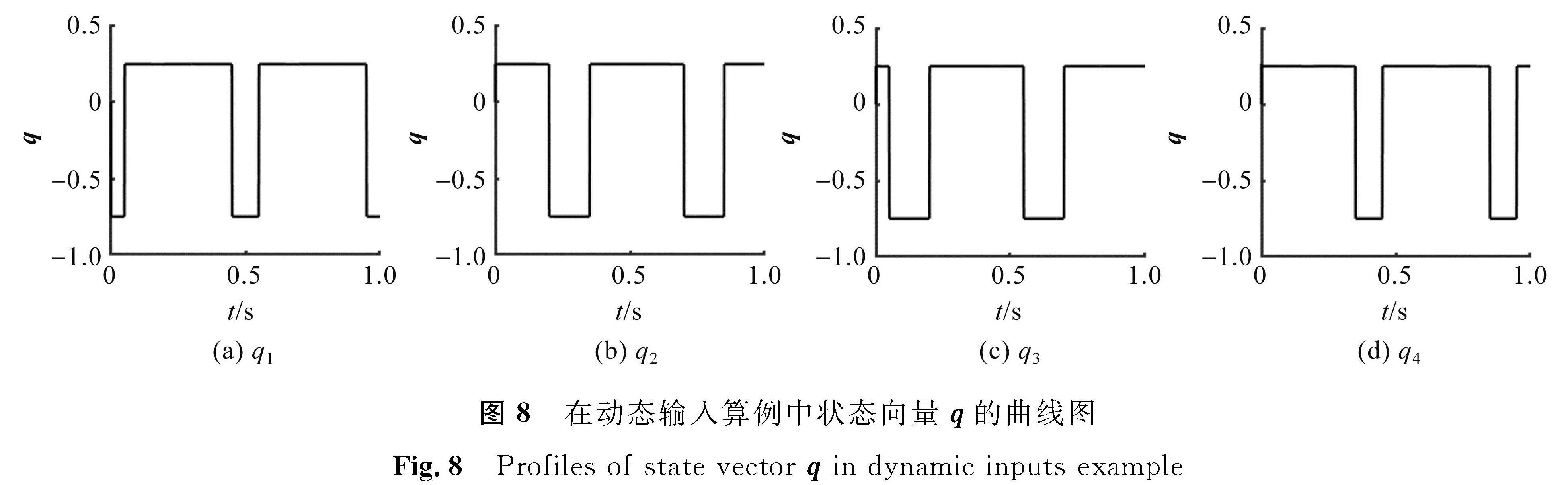
在动态输入算例中输入向量x的曲线图见图6。相应的参数设定为λ=109,δ=0.01,μ=0.1。p的初始值是随机的,并且根据定理1将q的初始值设为0。在动态输入算例中状态向量p的曲线图见图7。在动态输入算例中状态向量q的曲线图见图8。从图7和图8可以看出,状态向量p和q随着动态输入向量x周期性变化,从而找到新的赢家。在动态输入算例中输出向量r的曲线图见图9,将其与图6对比可以看出,本研究提出的分布式k -WTA模型可以在任何时刻找到正确的赢家。
4 结 语
本研究提出了一种新型分布式k -WTA模型来解决通信受限的智能体网络中的k -WTA问题。根据拉塞尔不变性原理,在不变集中将所提出的模型退化为现有的集中式k-WTA模型,并证明了本模型的全局渐进收敛性。静态输入和动态输入的两个数值算例验证了本研究所提模型的有效性和性能。在未来的研究中,将本模型扩展到复数域[20]可能是一个改进方向,而多机械臂的分布式协同运动可能是一个研究应用方向。
- [1] CHERRYK M, QIAN L L.Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks[J]. Nature, 2018,559(7714):370.
- [2] 吴倩,曹春杰.基于k-WTA的对抗样本防御模型研究[J].海南大学学报(自然科学版),2021,39(4):340.
- [3] ZHANG Y H, XIANG S Y, GUO X X, et al. The winner-take-all mechanism for all-optical systems of pattern recognition and max-pooling operation[J]. Journal of Lightwave Technology,2020,38(18):5071.
- [4] CHEN Z J, ZHANG J D, WEN S C, et al. Competitive neural network circuit based on winner-take-all mechanism and online hebbian learning rule[J]. IEEE Transactions on Very Large Scale Integration(VLSI)Systems,2021,29(6):1095.
- [5] MAJANIE, ERLANSON R, ABU-MOSTAFA Y S. On the k-winners-take-all network[J]. Advances in Neural Information Processing Systems,1988,1:1.
- [6] CALVERT B D, MARINOV C A. Another k-winners-take-all analog neural network[J]. IEEE Transactions on Neural Networks,2000,11(4):829.
- [7] LIU S B, WANG J. A simplified dual neural network for quadratic programming with its KWTA application[J]. IEEE Transactions on Neural Networks,2006,17(6):1500,1502.
- [8] HU X B, WANG J. An improved dual neural network for solving a class of quadratic programming problems and its k-winners-take-all application[J]. IEEE Transactions on Neural networks,2008,19(12):2022-2023.
- [9] WANG J. Analysis and design of a k-winners-take-all model with a single state variable and the heaviside step activation function[J]. IEEE Transactions on Neural Networks,2010,21(9):1496,1498.
- [10] LIU Q, DANG C, CAO J. A novel recurrent neural network with one neuron and finite-time convergence for k-winners-take-all operation[J]. IEEE Transactions on Neural Networks,2010,21(7):1140-1141.
- [11] PENG B, JIN L, SHANG M. Multi-robot competitive tracking based on k-WTA neural network with one single neuron[J]. Neurocomputing,2021,460:1.
- [12] QI Y M, JIN L, LUO X, et al. Robust k-WTA network generation, analysis, and applications to multiagent coordination[J]. IEEE Transactions on Cybernetics,2022,52(8):8515.
- [13] LIU M, ZHANG X Y, SHANG M S, et al. Gradient-based differential k-WTA network with application to competitive coordination of multiple robots[J]. IEEE/CAA Journal of Automatica Sinica,2022,9(8):1452.
- [14] LI S, ZHOU M C, LUO X, et al. Distributed winner-take-all in dynamic networks[J]. IEEE Transactions on Automatic Control,2016,62(2):577
- [15] JIN L, LI S. Distributed task allocation of multiple robots:a control perspective[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems,2016,48(5):693.
- [16] JIN L, LI S, LA H M, et al. Dynamic task allocation in multi-robot coordination for moving target tracking:a distributed approach[J]. Automatica,2019,100(7):75.
- [17] HESPANHA J P. Uniform stability of switched linear systems:extensions of LaSalle's invariance principle[J]. IEEE Transactions on Automatic Control,2004,49(4):470.
- [18] JADBABAIE A, LIN J, MORSEA S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control,2003,48(6):988.
- [19] ZHANG Y Y, LI S, WENG J. Distributed estimation of algebraic connectivity[J]. IEEE Transactions on Cybernetics,2022,52(5):3047.
- [20] 高畅,孔颖,胡汤珑.基于有限时间神经网络求解的时变复数矩阵方程[J].浙江科技学院学报,2022,34(5):409.
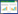 图 1 在静态输入算例中的通信拓扑
Fig.1 Communication topology in static inputs example
图 1 在静态输入算例中的通信拓扑
Fig.1 Communication topology in static inputs example