随着精准农业装备技术水平的提升,利用机器人进行稻田机械化除草因其无污染、劳动力需求低而受到广泛的关注[1-3]。近年来,国内外一些高校和农机科研单位针对传统大型水稻除草机器人存在的转向困难,只能在水稻未种植之前使用的问题,研制出了多种小型稻田行内除草机器人[4-6]。然而,小型除草机器人受自身体积及载重量的限制,存在着电池容量有限的问题,尤其对于水土共存的稻田环境,除草机器人运动阻力较大,除草作业所需的电量更多。这就导致在进行中大型稻田作业时,单个小型除草机器人无法在续航能力内完成全覆盖[7]除草任务。因此,需采用多机协同来降低单个小型除草机器人的耗电量。
作为提升机器人作业能力的关键技术之一,多机协同路径规划技术能将作业任务合理地分配给各个机器人,在降低每个机器人作业量的同时提升整体作业效率,目前被广泛应用于农机多机调度作业中。Trigui等[8]针对农业机器人任务分配问题,提出了基于分布式市场的算法和改进分布式市场的算法两种改进市场算法。Liu等[9]提出了一种丘陵山区农田全覆盖路径规划算法,将目标农田分割为多个规则无障碍子区域,并采用退火算法与混合搜索算法相结合的方式搜索子区域间最短遍历顺序。Li等[10]利用优化蚁群算法求解最优调度方法和最优卸货位置,为运输机械划分了动态时间窗并生成局部动态避障路径。为了提高农业运输机的工作效率,涂亚楠等[11]提出了一种基于蚁群算法的多机任务协同分配模型,降低了路径成本,避免出现超载问题。唐灿等[12]以最小化农业无人机转移路径长度为优化目标,利用Google-OR-Tools开源软件中的优化搜索策略算法求解航线调度及航次规划模型。
由于机插稻田中的秧苗整体呈行状排列,且各行间距相近,符合整数编码的特征。因此,可将稻田多机协同除草问题转化为以水稻行间过道为基础单元的任务分配问题。作为群智能优化算法,遗传算法(genetic algorithm,GA)因其优异的整数编码求解能力而被广泛运用于解决多机协同路径规划问题。但是传统遗传算法在求解多维复杂问题时存在着收敛速度慢、最优解质量较差、容易早熟等问题[13]。因此研究者针对遗传算法的交换和变异过程进行了改进,以增强遗传算法的求解能力。宫金良等[14]根据农田中的大型障碍物分布对农田进行切割,将其分解为多个无障碍子区域,提出了一种改进遗传算法求解各个子区域之间的遍历顺序; 李雯等[15]针对酿酒葡萄生长全过程中存在的多任务多农机调度需求,提出了一种自适应遗传算法(adaptive genetic algorithm,AGA),通过判断个体适应度与平均适应度的关系动态调整交换与变异概率。也有研究者通过融合其他算法的优势部分提升遗传算法的求解能力。Wang等[16]在遗传算法中引入可变邻域搜索算法来求解多旅行商问题; Liang等[17]针对多机器人多任务问题提出了一种引入惩罚策略的优化遗传算法,通过惩罚能量过剩的机器人来优化任务分配过程。
从上述研究可以看出,优化遗传算法能有效解决多机协同作业问题,但是在求解复杂编码问题时仍存在着最优解质量和鲁棒性优化较差的情况。因此,本研究根据机插稻田的特点采用以水稻行间过道为基础单元的作业区域分割方法,将最小化能耗最高的除草机器人的移动距离作为优化目标,并利用多染色体优化遗传算法(multi-chromosome optimized genetic algorithm, MGA)来进行多机路径规划,以降低能耗最高的除草机器人的移动距离,从而保证多机协同除草任务能够顺利完成。
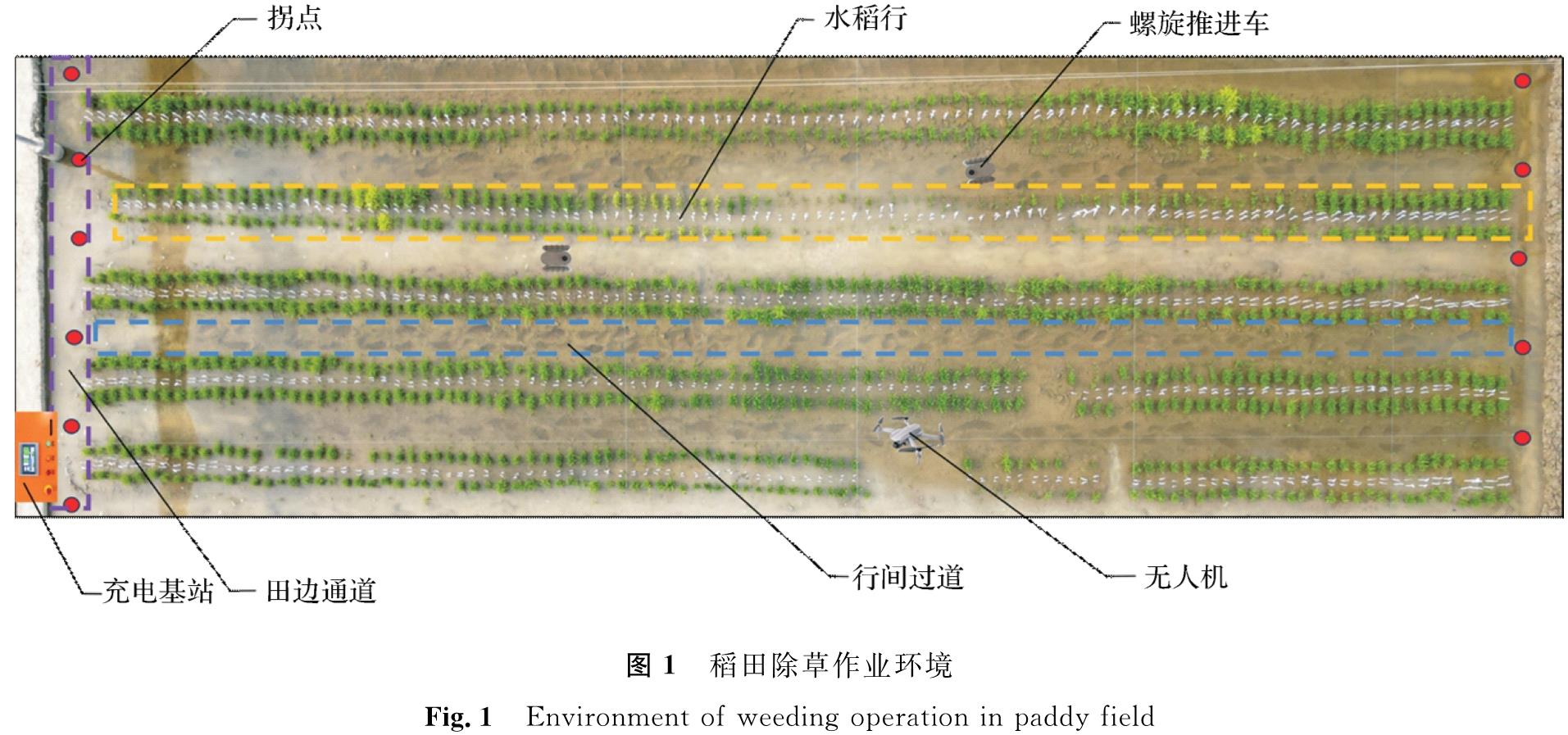
1 多机协同除草作业问题分析1.1 问题描述在进行多机协同除草作业时,稻田除草作业环境如图1所示。
由图1可知,稻田除草作业环境主要由以下七部分构成。
1)螺旋推进车:螺旋推进车是一种小型稻田行间除草机器人,该车辆通过螺旋滚筒结构翻拌稻田土壤使水体浑浊,从而阻止杂草进行光合作用。
2)无人机:利用无人机拍摄稻田图像,通过俯拍图像获取水稻秧苗分布情况及其他相关参数。
3)水稻行:由水稻秧苗拟合而成,属于螺旋推进车应避免碰撞的障碍物。
4)行间过道:水稻行间过道指的是水稻行之间或水稻行与横向田埂间的可通行过道,是螺旋推进车进行除草作业的主要区域。
5)田边通道:田边通道指的是纵向田埂与水稻行侧边之间的区域,是螺旋推进车进行跨行移动的唯一通道。
6)拐点:拐点是指螺旋推进车驶入水稻行间过道的转弯点,位于田边通道中,根据其在稻田中的位置,可以分为左侧拐点和右侧拐点。
7)充电基站:位于田边通道旁的地头侧,为螺旋推进车提供充电服务; 同时,充电基站也是螺旋推进车作业时的出发点和结束点。
因此,多机协同路径规划问题具体表述如下:在稻田中,调用一组螺旋推进车进行除草作业,设置多个充电基站为螺旋推进车提供充电和停靠服务; 在保证整体除草效果的前提下,使能耗最高的螺旋推进车的移动距离最小化; 要求若干台螺旋推进车从停靠的充电基站出发,协同遍历所有水稻行间过道; 在完成除草任务之后,螺旋推进车就近返回系统分配的充电基站停靠充电,等待下次除草任务开始。
针对螺旋推进车除草过程,特作以下约定:
1)在进行除草作业时,每个水稻行间过道只允许一台螺旋推进车进行一次遍历。
2)在完成除草作业返回充电基站时,允许螺旋推进车通过已完成除草作业的水稻行间过道返回充电基站。
3)螺旋推进车只能通过稻田两侧的田边通道进行跨行移动。
4)螺旋推进车作业过程中暂不考虑其故障和突遇动态障碍物的情况,此类特殊情况由中断处理模块统一处理。
5)所有螺旋推进车的型号相同,作业能力、续航时间、作业速度等参数相似。
1.2 模型构建为了方便建立多机协同路径规划模型,设定相关参数如下。
1)集合参数:螺旋推进车集合R={r1,r2,…,rnr},其中nr为螺旋推进车的数量; 充电基站集合B={b1,b2,…,bnb},其中nb为充电基站的数量; 水稻行间过道集合L={l1,l2,…,lnl}; 左侧拐点集合Q={q1,q2,…,qnl}; 右侧拐点集合P={p1,p2,…,pnl}。由于左、右侧拐点与水稻行间过道存在着一一对应的关系,因此三者数量皆为nl。
2)距离参数:螺旋推进车通过水稻行间过道所需的移动距离设为dl; 从充电基站b到左侧拐点q所需的移动距离设为 db q; 从充电基站b到右侧拐点p所需的移动距离设为 db p; 从左侧拐点q到左侧拐点q'所需的移动距离设为 dq q'; 从右侧拐点p到右侧拐点p'所需的移动距离设为 dpp'。
3)对应关系:在作业开始前,螺旋推进车r停靠在充电基站b,其对应关系记录为S1={b→r}; 左右侧拐点(q,p)与水稻行间过道l的对应关系记录为S2={(q,p)→l}。
4)事件参数:xrbq表示螺旋推进车r从充电基站b出发移动到左侧转弯点q,或从左侧转弯点q移动到充电基站b充电; yrbp表示螺旋推进车r从充电基站b出发移动到右侧拐点p,或从右侧拐点p回归充电基站b充电; zrl表示螺旋推进车r通过水稻行间过道l进行除草作业; urqq'表示螺旋推进车r通过左侧田边通道从拐点q移动到拐点q'; vrqq'表示螺旋推进车r通过左侧田边通道从拐点p移动到拐点p'。若事件发生记录为1; 反之则记录为0。
根据上述参数可以将螺旋推进车的移动距离
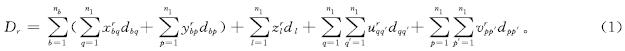
由于螺旋推进车是在行进的同时进行除草作业的,且螺旋推进车转弯时产生的额外电量消耗可忽略不计,因此能耗最高的螺旋推进车即是移动距离最长的螺旋推进车。故目标函数可表示为
min{maxDr|r∈R}。 (2)
同时,多机除草系统应满足以下约束条件:
nb≥nr; (3)
max{Dr|r∈R}≤Dmax。 (4)
式(4)中:Dmax为螺旋推进车在保留应急电量下的最大移动距离。

式(3)表示为了节约成本,充电基站数量不应大于螺旋推进车数量; 式(4)表示为了保证除草任务能够顺利完成,能耗最高的螺旋推进车的移动距离应小于螺旋推进车在保留应急电量下的最大移动距离; 式(5)表示在除草作业时,每条水稻行间过道都必须被遍历且每条水稻行间过道只被遍历一次。
2 多染色体优化遗传算法2.1 多染色体遗传算法设计遗传算法是通过模拟自然界种群进化的随机搜索算法,在将搜索对象转化为染色体编码后,通过选择、交换、变异操作不断推动种群迭代进化,从而获得适应度最高的最优解。针对传统遗传算法难以求解复杂多机协同问题的情况,本研究根据多机协同路径规划模型引入多染色体概念来设计多染色体遗传算法。
2.1.1 多染色体编码本研究根据各螺旋推进车的遍历顺序构建多个染色体。由于螺旋推进车的运动路径包含水稻行间过道与充电基站两个不同部分,因此在编码过程也应映射为两种不同的编码。对此,本研究采用多参数联合编码与实数编码相结合的方式,对螺旋推进车的作业路径进行编码。在单个螺旋推进车的路径编码中,染色体两端应为充电基站编码,中间为水稻行间过道编码。由于螺旋推进车开始时停靠的充电基站是一定的,由上一次除草作业的最终停靠点决定,而最终停靠的充电基站是可以自由选取的,故作为出发点的充电基站不计入编码,直接从系统中读取。具体的编码过程如下:
首先,定义第一种由行间过道集合L编码构成的参数1,2,3,…,n1。然后,第二种参数同样采用实数编码,由充电基站集合B编码构成,但是为了与行间过道编码进行区分,设定为实数n1+1,n2+2,…,nl+nb。
在作业系统中,各螺旋推进车的染色体相互影响。根据多机协同路径规划模型中的式(4)约束,各螺旋推进车的染色体必须覆盖所有的水稻行间过道编码,同时每个水稻行间过道编码只能出现一次。
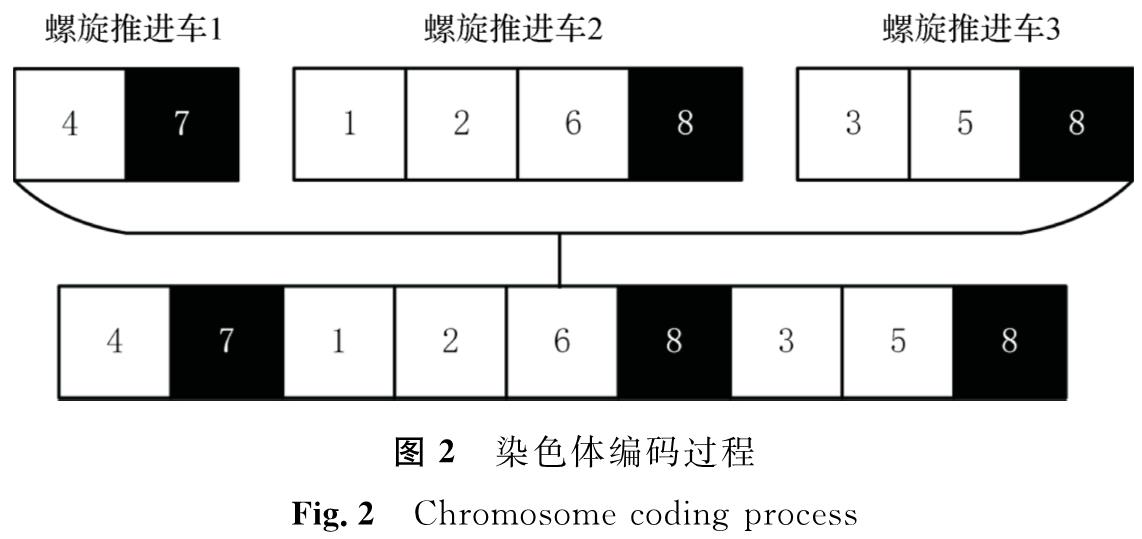
假设n1=6,nr=3,nb=2,则染色体编码过程如图2所示。为了方便后期的迭代,将染色体群按照螺旋推进车的编号顺序进行组合,形成一个整体编码。
2.1.2 设计适应度函数
适应度函数表示个体或解的优劣性。在多机协同全覆盖路径规划模型中,个体的优劣性主要取决于能耗最高的螺旋推进车的移动距离max{Dr|r∈R}的大小,且与适应度函数f成反比例关系:
f=1/(max{Dr|r∈R})。 (6)
2.1.3 选择操作在遗传算法中,遗传操作是推动群体进化的关键步骤,主要包括选择、交换和变异3个过程。根据多机协同路径规划模型选用轮盘赌的方式进行父母本选择操作,以增大产生优秀后代的概率。个体 i 被选中的概率

式(7)中:fi为个体i的适应度函数值; M为遗传算法群体中的个体数量。
2.1.4 设置终止条件当迭代次数到达设定参数Eepoch或连续迭代一定次数最优解未发生改变时则停止迭代,输出此时的历史最优解。
2.2 遗传算法优化策略遗传算法要完成遗传进化过程,在选择操作后还需进行交换与变异操作。但由多个染色体组合构成的整体染色体结构复杂,采用传统的交换与变异方式会大幅度改变染色体结构,难以保留并传承优质的遗传信息。因此本研究针对多染色体结构优化交换与变异过程,以提升算法的搜索能力。
2.2.1 逐代竞争机制传统遗传算法通过交换概率来控制交换过程的发生:当系统生成的随机数小于交换概率时,算法对选择过程中选取的两个整体染色体进行交换操作; 反之,则跳过交换过程直接保留两个父本染色体。较大的交换概率能够加快新个体的产生速度,但也可能破坏本身的优势群体,导致算法的随机性过大,进而影响算法的收敛速度; 反之,较小的交换概率能够较好地保存优势群体,但整体进化速度偏慢,导致算法运行时间过长。
针对以上问题,许多研究者采用自适应交换概率来平衡算法随机性和进化速度之间的关系。但由于整体染色体结构复杂,在交换过程中产生的子代优于父代的可能性较低,导致算法整体的进化速度缓慢,且会造成算法的最优解质量偏低。因此,本研究改变凭借交换概率pc来判断是否进行交换的方法,在种群完成选择操作后直接进行交换操作,但并不直接保留子代染色体,而是纵向对比两个父本染色体与两个子代染色体之间的适应度关系,以保留适应性较强的两个染色体。在保留优势群体的基础上加快新个体的产生速度。
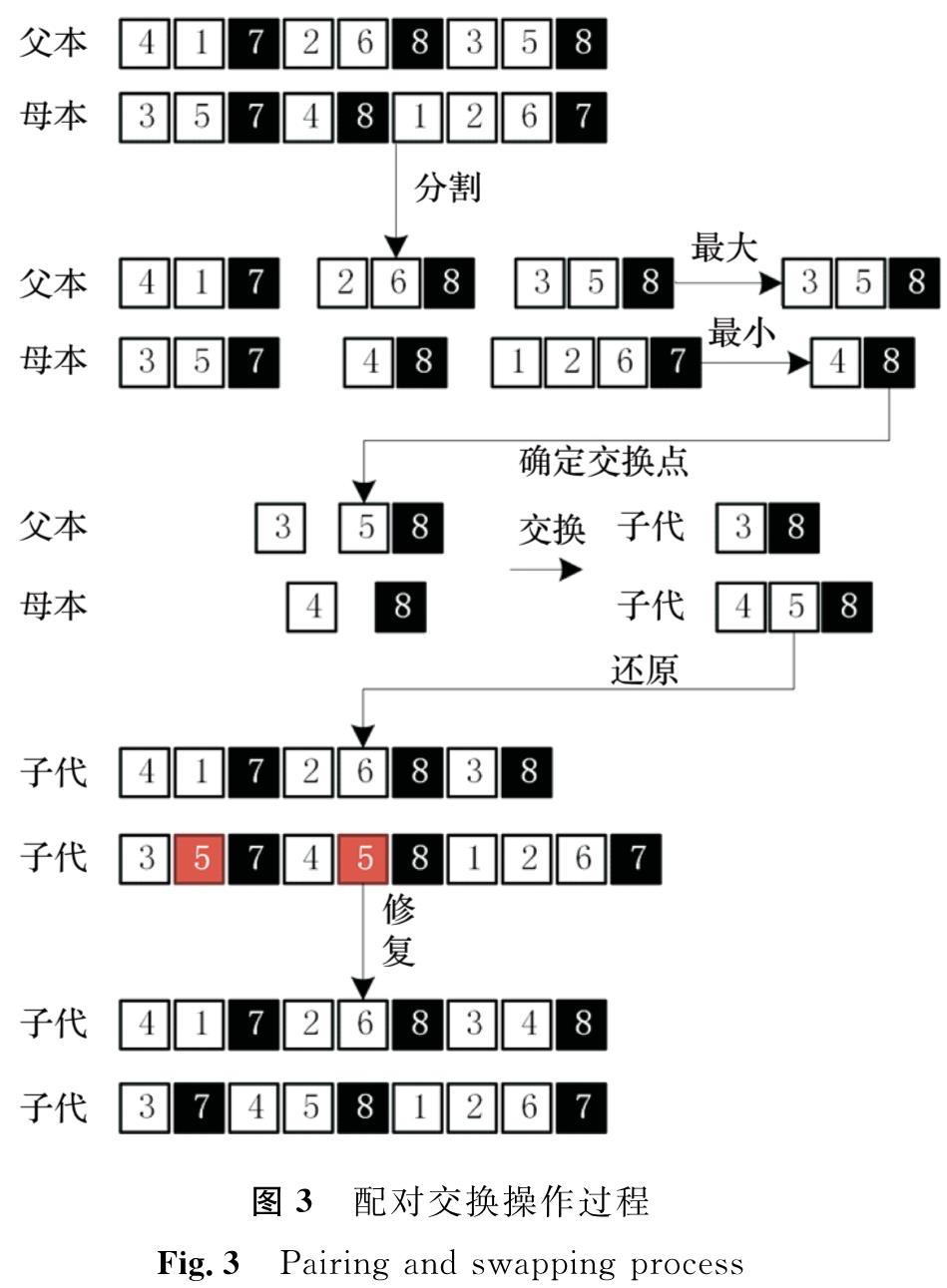
2.2.2 配对交换机制针对交换过程会大幅改变整体染色体结构的问题,本研究采用配对交换机制来优化交换过程。其具体过程如下:
1)分别随机选取一个染色体作为父本,一个作为母本。
2)根据充电基站编码的位置对染色体进行分割,还原为多染色体状态。
3)通过计算两个染色体群中的各个染色体对应的路径长度,选取父本中路径长度最大的染色体和母本中路径长度最小的染色体进行配对。
4)在配对的两个染色体的水稻行间过道编码区分别随机生成一个交换点,在交换点处进行分割。
5)根据分割情况交换配对染色体的编码,生成新的染色体。
6)将染色体群重新组合生成新的整体编码。
7)根据多机协同作业模型的约束条件修复整体编码,完成交换过程。
具体配对交换操作过程如图3所示。
2.2.3 自适应变异算子
在传统遗传算法的搜索过程中,不可避免地会陷入局部最优解[18],需增加算法随机性以帮助其跳出局部最优解。相较于搜索前期,遗传算法在搜索过程的后期往往会出现搜索迟钝的情况,更容易陷入局部最优解[19]。为了帮助遗传算法脱离局部最优解,加快算法收敛速度,引入自适应变异算子pe,将变异算子与迭代次数相结合:
pe=(ep0)/(Eepoch)。 (8)
式(8)中:p0为初始设定的变异权重; e为当前迭代次数。
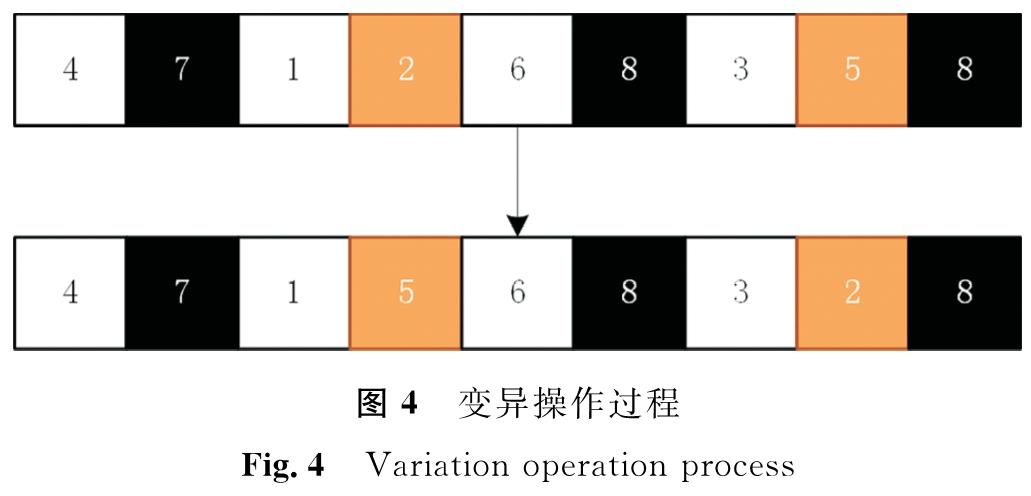
具体的变异操作过程如图4所示。
需要注意的是,染色体编码中存在两类不同编码,即水稻行间过道编码和充电基站编码。因此,在变异过程中分别对这两种编码进行独立的变异操作。具体变异步骤如下:
1)生成一个[0,1]范围内的随机数,若产生的随机数小于或等于变异概率pe,则进行一次变异操作。重复此步骤直到产生的随机数大于变异概率函数。
2)每进行一次变异操作,生成一个[1,nl+nr]范围内的随机整数。若该随机数对应的编码为充电基站编码则执行步骤3); 反之则执行步骤4)。
3)将选中的充电基站编码随机替换为其他充电基站编码。
4)再次产生一个[1,nl+nr]范围内的随机整数,交换两个随机数对应的编码。
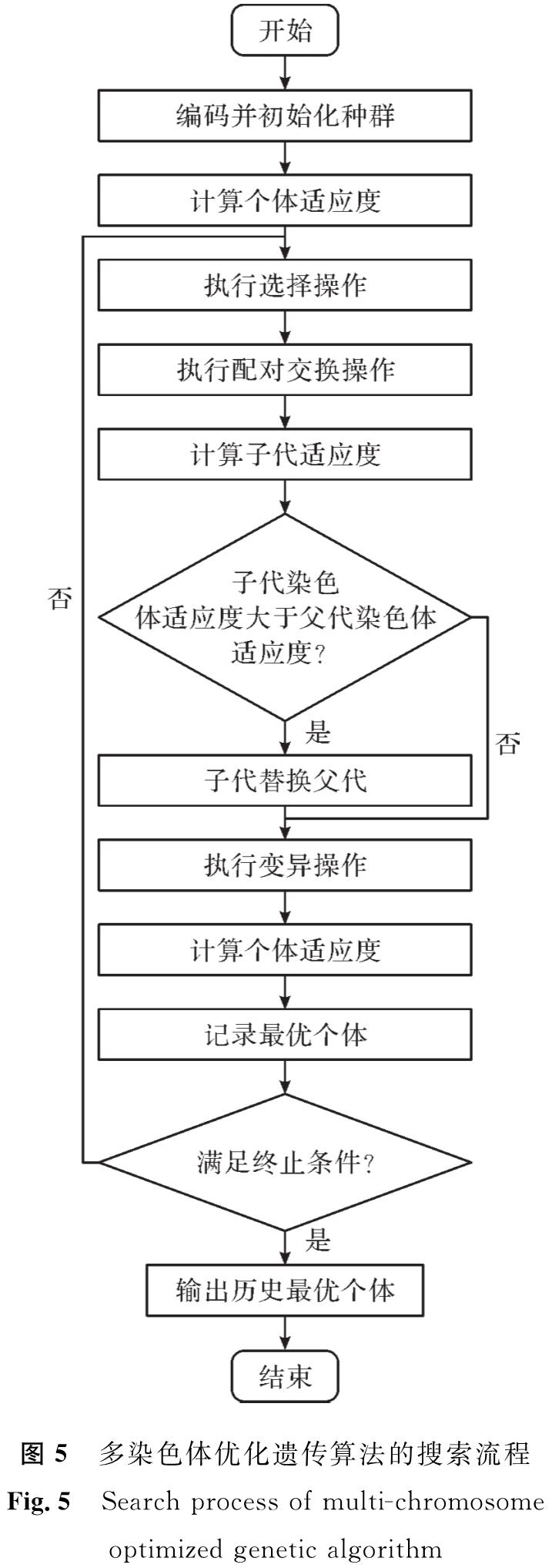
最终构建的多染色体优化遗传算法的搜索流程如图5所示。
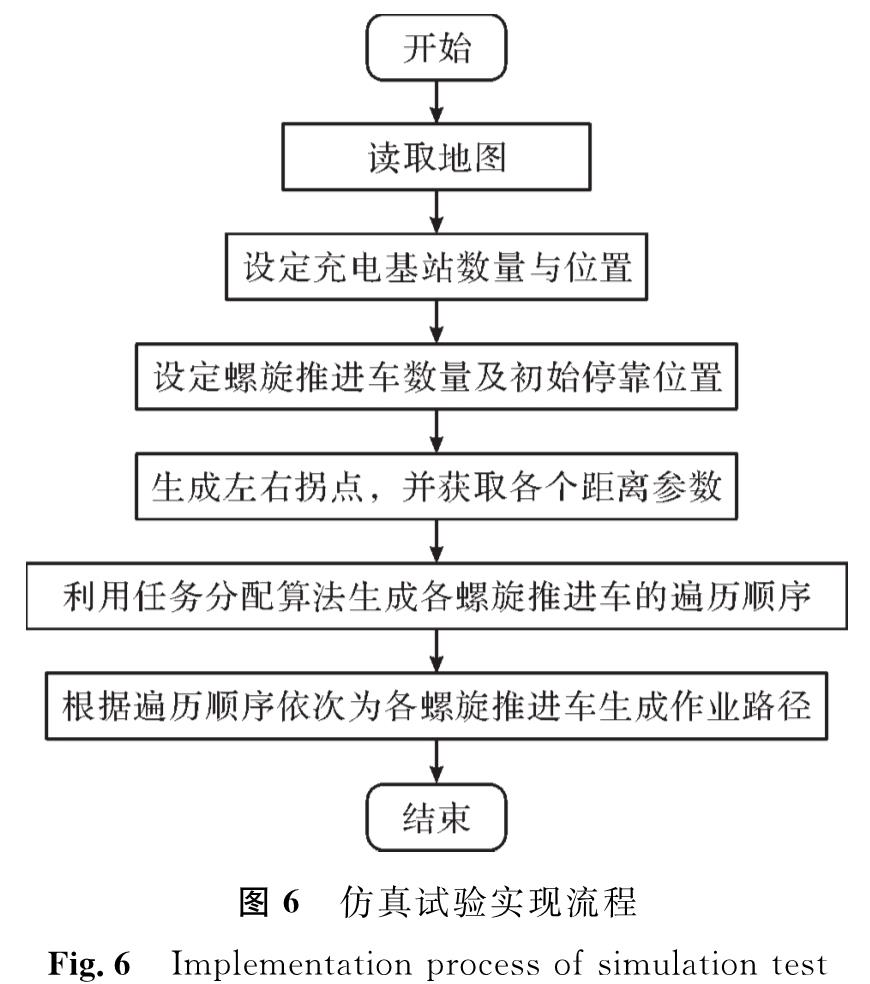
3 试验与结果分析为验证多染色体优化遗传算法的可行性与优越性,分别对其进行不同田形地图仿真试验和稻田栅格地图仿真试验。试验采用3.7版本的python语言编写,使用的计算机配置如下:操作系统为Windows 10,处理器为i7-9750H,主频为2.59 GHz,运行内存为16 GB。仿真试验实现流程如图6所示。
3.1 不同田形地图仿真试验
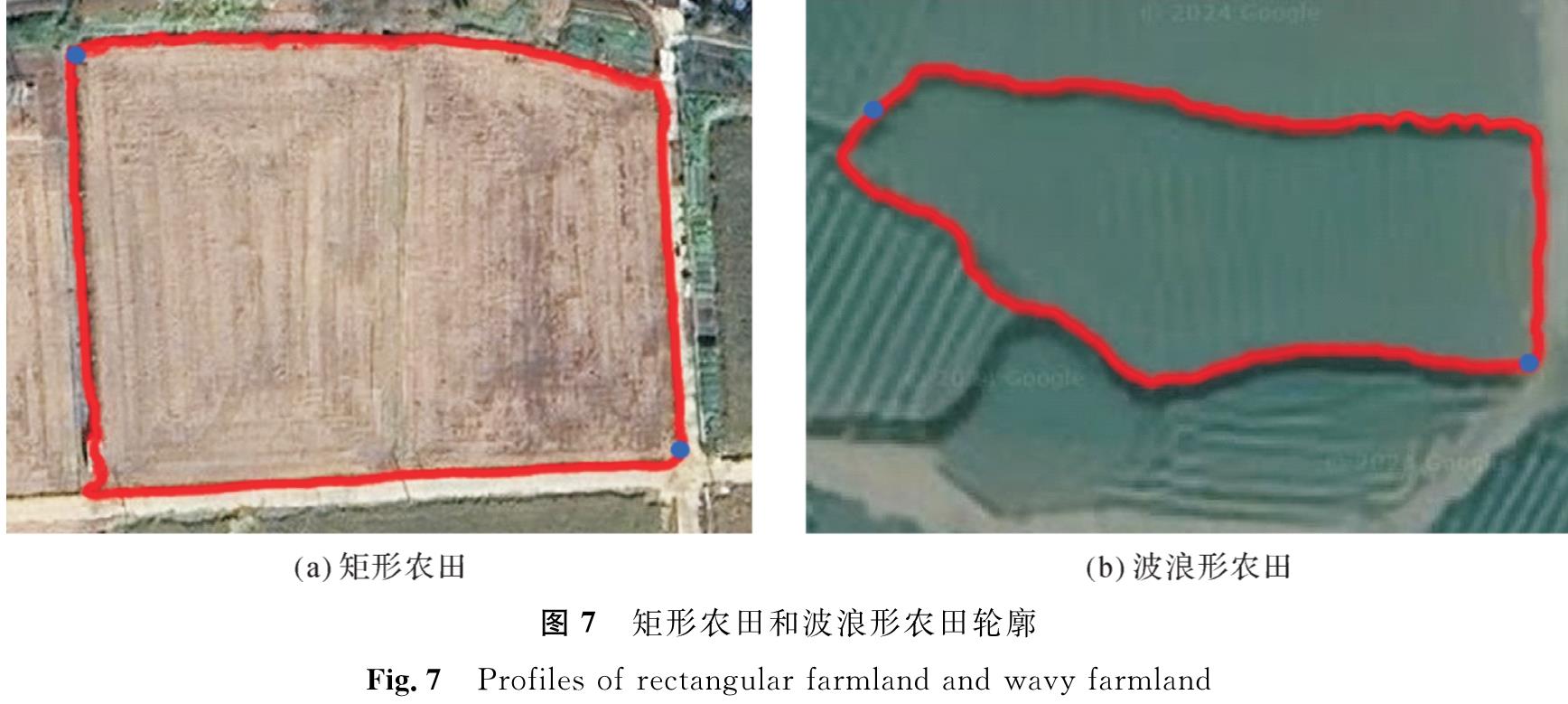
在不同地区的不同地形下,中国的农田形状和大小差异明显,但总体可分为矩形和波浪形两种类型。矩形稻田是平原水稻种植农田的主要田形,其内种植的水稻行长度相近; 波浪形稻田是丘陵断面梯田的常见田形,其内种植的水稻行长度变化较大。通过Google卫星地图获取矩形农田和波浪形农田轮廓,如图7所示,并在农田轮廓内部等距插入规则水稻行作为障碍物,在左上角和右下角分别设置两个充电基站作为螺旋推进车的出发点和停靠点,以验证多染色体优化遗传算法在不同田形中的最优解质量与鲁棒性。
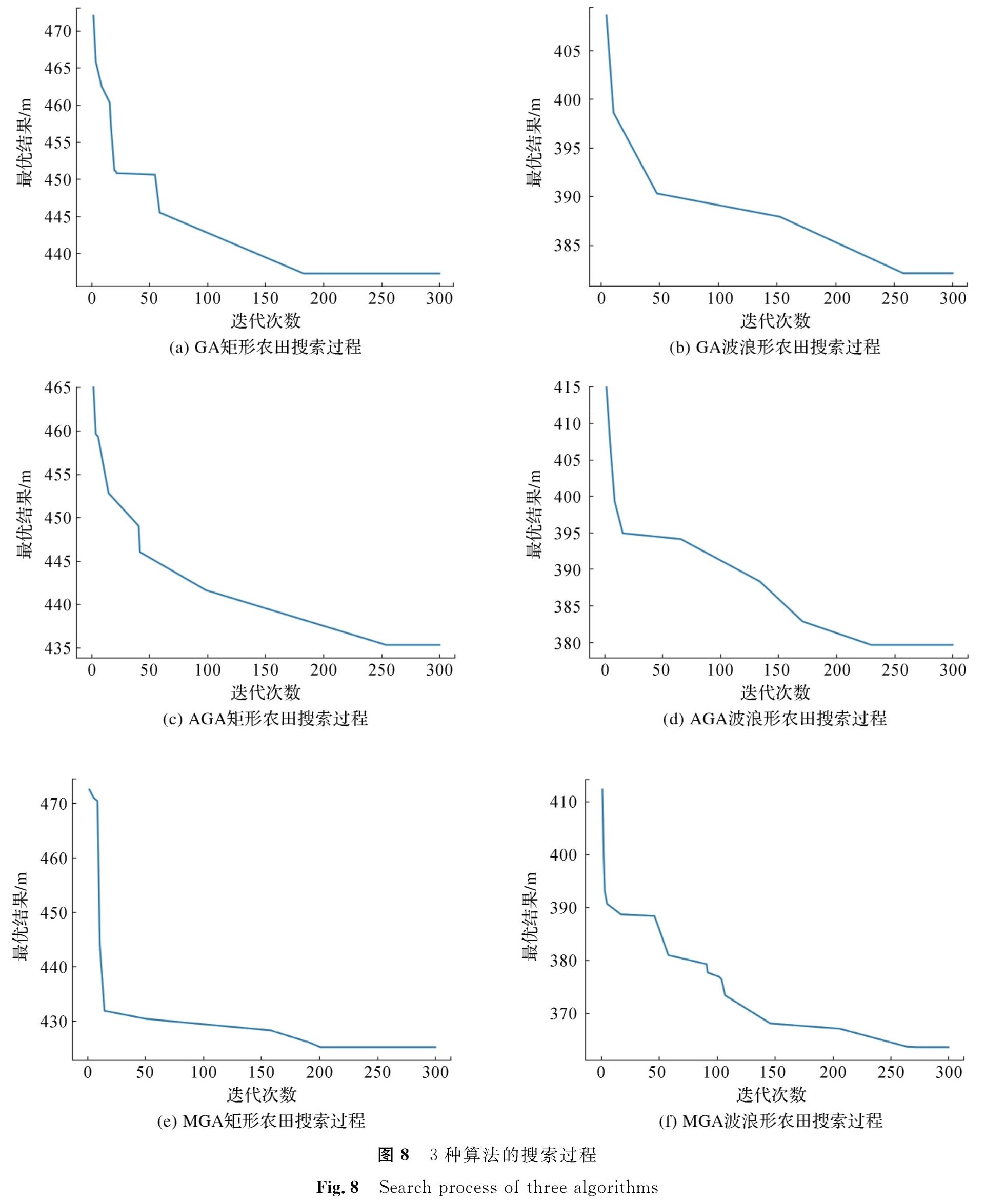
读取矩形农田地图和波浪形农田地图中水稻行间过道长度、充电基站位置、拐点位置等数据,分别利用本研究提出的多染色体优化遗传算法、传统遗传算法和自适应遗传算法搜索最优遍历顺序,同时为了保证对比的公平性,限定3种算法都迭代300次。3种算法的搜索过程如图8所示。
从图8(a)、(b)中可以看出,GA在搜索过程中最优结果的进化次数较少,并且进化幅度存在着较大的随机性; 从图8(c)、(d)中可以看出,AGA在搜索过程中整体较为稳定,但最优解质量相对较差; 从图8(e)、(f)中可以看出,MGA在搜索过程中的进化次数更多且更密集,说明逐代竞争机制和配对交换机制能在保留优势种群的同时加快了算法的进化速度,进而提升算法的最优解质量。在接近收敛时,MGA能通过不断增大的变异概率跳出局部最优解,从而提升算法的最优解质量和鲁棒性。
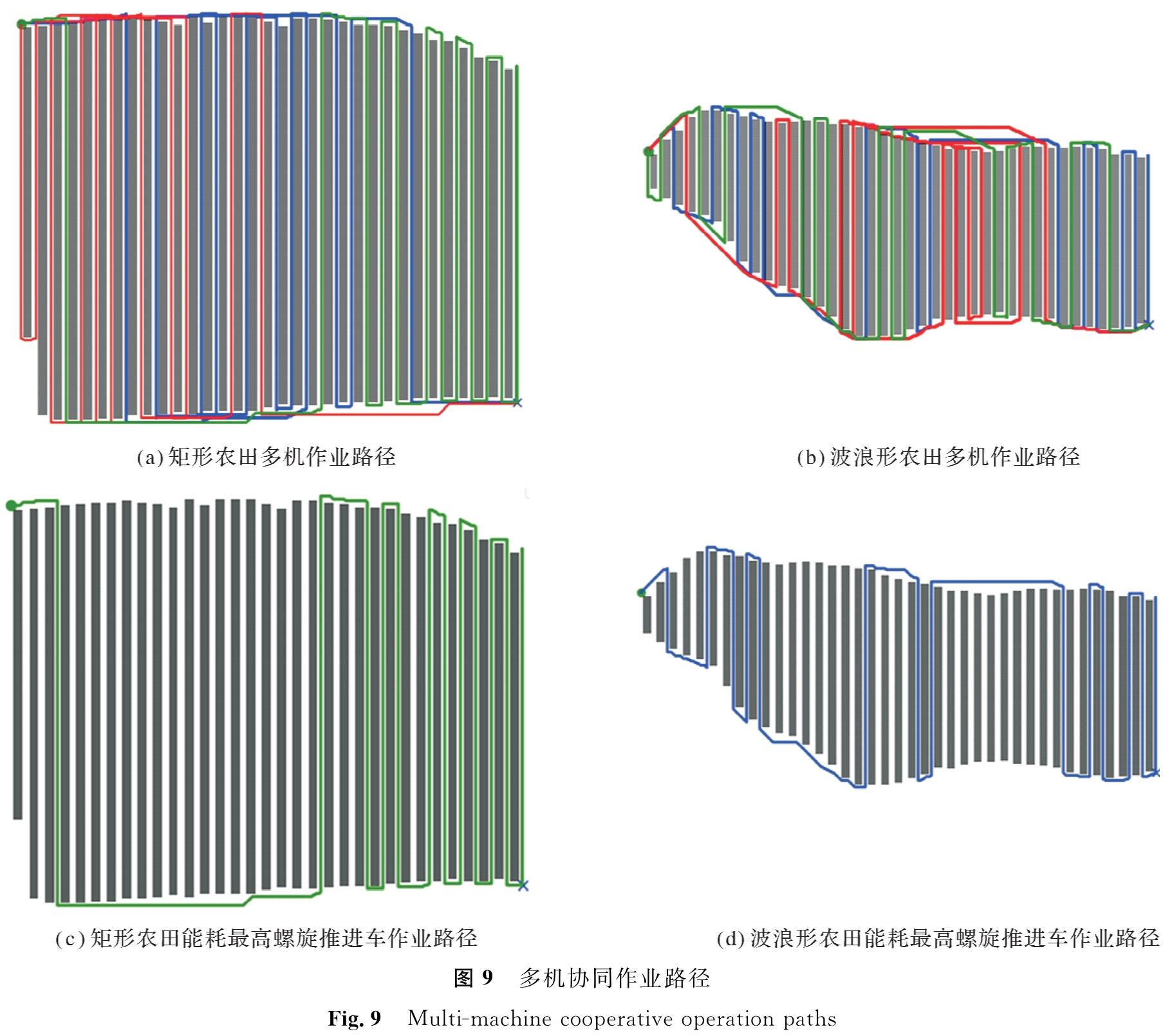
利用MGA分别在矩形农田和波浪形稻田中生成任务分配方案,并绘制出多机协同作业路径,如图9所示。
从图9(a)可以看出,由于矩形稻田中水稻行间过道长度差距不大,3辆螺旋推进车遍历的水稻行间过道数量相似。在除草过程中,3辆螺旋推进车协同遍历了所有水稻行间过道,且每个行间过道仅通过了一辆螺旋推进车,满足式(4)的约束要求。从图9(c)中可以看出,作为优化的主要目标,能耗最高的螺旋推进车3的遍历顺序符合从左到右的规律,减少了其跨行移动距离。从图9(b)和图9(d)可以看出,在波浪形稻田中,水稻行间过道的长度差距较大,因此螺旋推进车的作业路径分布更加均匀,不再集中于同一区域,但仍保持了与矩形稻田中相似的路径特点。
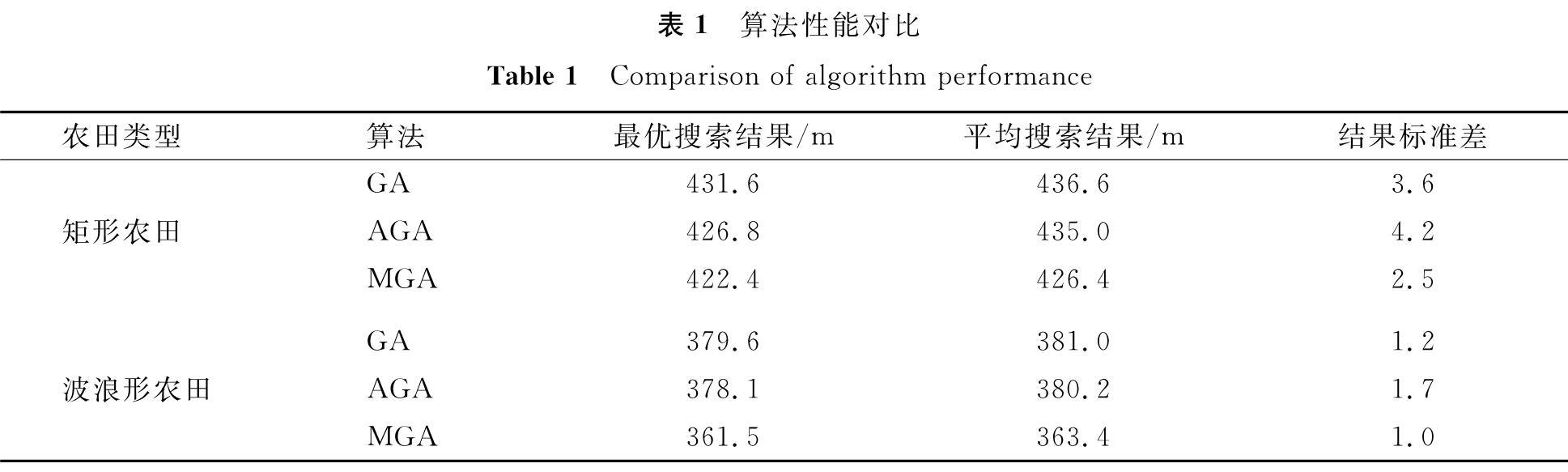
将上述搜索过程重复5次,并对比3种算法的性能,其搜索结果记录于算法性能对比表(表1)中。
由表1可知:由于逐代竞争机制和配对交换机制的使用,在矩形农田中MGA的最优搜索结果(即能耗最高的螺旋推进车的移动距离)相较于GA和AGA分别缩短了2.1%和1.0%,MGA的平均搜索结果相较于GA和AGA分别缩短了2.3%和2.0%; 在波浪形稻田中MGA的最优搜索结果相较于GA和AGA分别缩短了4.8%和4.4%,MGA的平均搜索值相较于GA和AGA分别缩短了4.6%和4.4%。同时,由于自适应变异算子的使用,MGA在矩形农田中的结果标准差比GA和AGA分别降低了30.6%和40.5%; 在波浪形稻田中MGA在矩形农田中的结果标准差比GA和AGA分别降低了16.7%和41.2%。
从上述数据可以看出,不论是在哪一种田形中,MGA都拥有更高的最优解质量和鲁棒性,能够有效缩短能耗最高的螺旋推进车的移动距离,满足多机协同作业模型的优化目标。尤其在面对差异性更大的波浪形稻田时,MGA的优势更加明显。
3.2 实际稻田地图试验相较于人工生成的规则矩形障碍,实际稻田中的秧苗分布更加复杂多样。因此,本研究利用无人机获取稻田秧苗的真实分布,并生成栅格地图,如图 10所示。在稻田栅格地图的左下角和右上角设置了2个充电基站作为出发点和终止点。同时,根据稻田的面积,选用3辆螺旋推进车即可满足多机协同除草作业的要求。
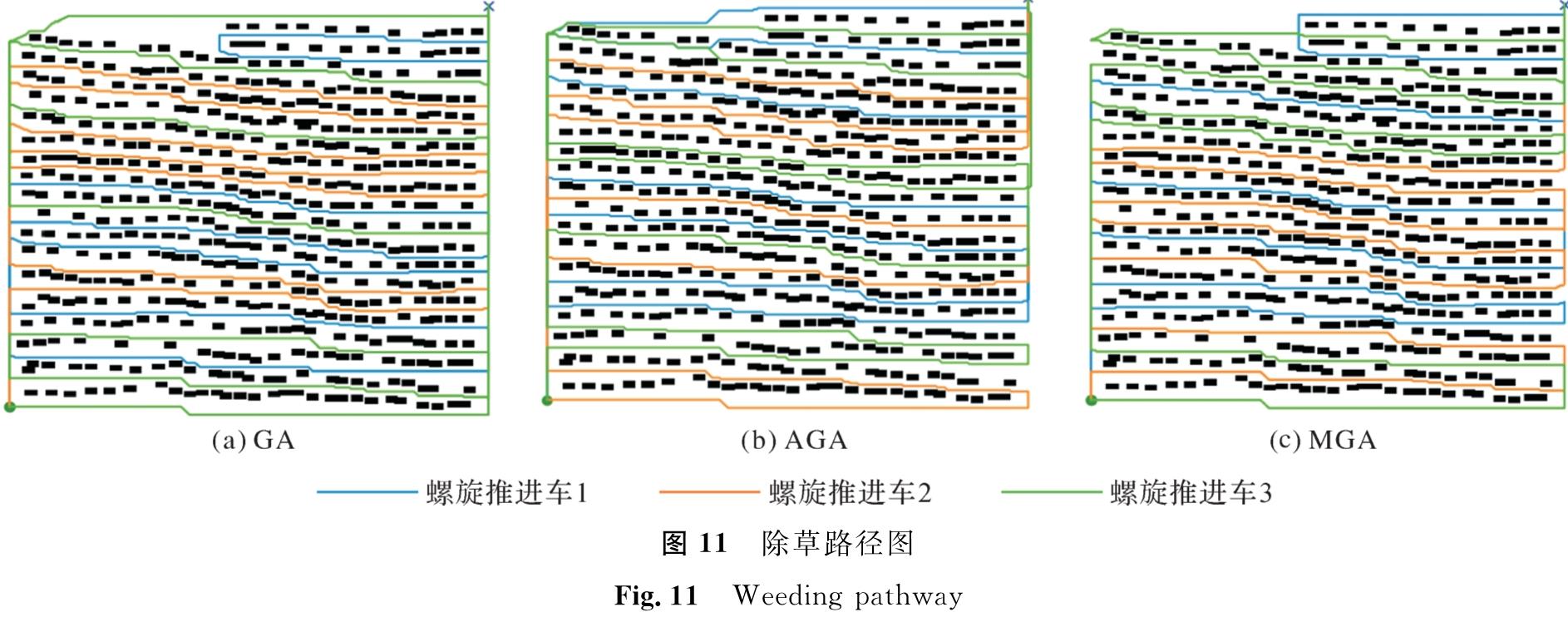
为了验证MGA在稻田栅格地图中的多机协同路径规划能力,利用GA、AGA和MGA分别生成除草路径图,见图 11。同时,将5次试验生成的路径数据记录在栅格地图算法性能对比表中,见表2。
表2 栅格地图算法性能对比
Table 2 Comparison of algorithm performance of grid maps
表2 栅格地图算法性能对比
Table 2 Comparison of algorithm performance of grid maps
由图 11可知,3种算法生成的协同作业路径都满足多机协同路径规划模型的相应约束。然而,相较于MGA,GA和AGA生成的作业路径来回往复情况更加明显,大大增加了螺旋推进车的跨行移动距离,造成了电能的浪费,不符合多机协同作业模型的优化目标。由表2可知,MGA中能耗最高的螺旋推进车的工作距离较GA缩短9.7%,较AGA缩短8.0%,证明逐代竞争机制和配对交换机制能有效优化算法的最优解质量; 此外,MGA生成螺旋推进车群的平均路径长度较GA缩短6.1%,较AGA缩短3.8%,证明MGA在使能耗最高的螺旋车的移动距离最小化的同时也能够带动系统整体的移动距离降低。MGA多次搜索结果的标准差比GA和AGA分别降低34%和40%,证明自适应变异算子能有效提升算法的鲁棒性。相较于不同田形地图仿真试验结果,在稻田栅格地图中,MGA减少能耗最高的螺旋推进车的移动距离的效果更加明显。
4 结 论本研究为解决小型稻田除草机器人由于续航能力不足而无法完成大面积作业任务的问题,以螺旋推进车为研究载体,以使能耗最高的螺旋推进车的移动距离最小化为优化目标,提出了一种基于多染色体优化遗传算法的多机协同路径规划方法,并进行了不同田形的地图仿真试验和稻田栅格地图仿真试验。根据试验结果,得出以下结论:
1)由于逐代竞争机制和配对交换机制的运用,MGA在不同田形地图和稻田栅格地图中多次试验生成的能耗最高的螺旋推进车的移动距离低于GA和AGA,证明在不同田形、不同秧苗分布的稻田中,MGA的最优解质量均优于GA和AGA,能够有效降低能耗最高的螺旋推进车的移动距离,减少其作业能耗。
2)由于自适应遗传算子的运用,在不同田形地图和稻田栅格地图仿真试验中,MGA多次试验生成结果的标准差低于GA和AGA,证明在不同田形、不同秧苗分布的稻田中,MGA的鲁棒性均强于GA和AGA,能够保证每次的搜索结果都近似最优解,有效地保证了系统的稳定性。
然而,在试验中我们也发现,由于优化目标为最小化能耗最高的螺旋推进车的移动距离,未被关注的其余螺旋推进车存在懈怠现象,即在能耗最高的螺旋推进车的移动距离保持不变的情况下,其余螺旋推进车的移动距离优化结果未被充分记录,导致算法生成的多机协同路径规划方案在缩短机器人平均工作距离方面尚有改进空间。未来的研究将通过增加其他相关优化目标,以调整比例权重的方式来构建更优的稻田除草机器人多机协同路径规划模型。
- [1] 沈国辉,梁帝允.中国稻田杂草识别与防除[M].上海:上海科学技术出版社,2018.
- [2] 邢钦淞,丁素明,薛新宇,等.智能田间除草机器人发展现状研究[J].中国农机化学报,2022,43(8):173.
- [3] 孙君亮,闫银发,李法德,等.智能除草机器人的研究进展与分析[J].中国农机化学报,2019,40(11):73.
- [4] LIU C, YANG K, CHEN Y, et al. Benefits of mechanical weeding for weed control, rice growth characteristics and yield in paddy fields[J]. Field Crops Research, 2023, 293:108852.
- [5] TANG H, XU C, WANG Q, et al. Analysis of the mechanism and performance optimization of burying weeding with a self-propelled inter row weeder for paddy field environments[J]. Applied Sciences-Basel, 2021, 11(21):9798.
- [6] 杨生旺.新型稻田微型螺旋推进除草机的设计与试验[D].杭州:浙江科技学院,2022.
- [7] TANG F. Coverage path planning of unmanned surface vehicle based on improved biological inspired neural network[J]. Ocean Engineering, 2023, 278:114354.
- [8] TRIGUI S, KOUBAA A, CHEIKHROUHOU O, et al. A distributed market-based algorithm for the multi-robot assignment problem[J]. Procedia Computer Science, 2014, 32(12):1108.
- [9] LIU T, LI J, YANG S X, et al. Optimal coverage path planning for tractors in hilly areas based on energy consumption model[J]. International Journal of Robotics & Automation, 2023, 38(1):20.
- [10] LI S, ZHANG M, WANG N, et al. Intelligent scheduling method for multi-machine cooperative operation based on NSGA-III and improved ant colony algorithm[J]. Computers and Electronics in Agriculture, 2023, 204:107532.
- [11] 涂亚楠,侯晓晓.农业运输机械田间路径协同分配模型研究[J].农机化研究,2024,46(9):53.
- [12] 唐灿,宗望远,黄小毛,等.农用无人机多机多田块作业路径规划算法[J].华中农业大学学报,2021,40(5):187.
- [13] CHAKRABORTY S, ELANGOVAN D, GOVINDARAJAN P L, et al. A comprehensive review of path planning for agricultural ground robots[J]. Sustainability, 2022, 14(15):9156.
- [14] 宫金良,王伟,张彦斐,等.基于农田环境的农业机器人群协同作业策略[J].农业工程学报,2021,37(2):11.
- [15] 李雯,倪锡涛.酿酒葡萄生长全过程多任务多农机调度研究[J].农机化研究,2024,46(5):262.
- [16] WANG Y, LU X, SHEN J. Improved genetic algorithm(VNS-GA)using polar coordinate classification for workload balanced multiple traveling salesman problem(MTSP)[J]. Advances in Production Engineering & Management, 2021, 16(2):173.
- [17] LIANG L, ZHU L, JIA W, et al. Multirobot task planning method based on the energy penalty strategy[J]. Applied Sciences-Basel, 2023, 13(8):4887.
- [18] 陈岁繁,王浈元,李其朋.基于改进蚁群优化算法的AGV路径规划[J].浙江科技学院学报,2024,36(1):59.
- [19] 赵睿琦.基于改进多目标遗传算法的变截面涡旋盘优化设计[J].机电信息,2023(6):31.
 图 1 稻田除草作业环境
Fig.1 Environment of weeding operation in paddy field
图 1 稻田除草作业环境
Fig.1 Environment of weeding operation in paddy field