二次规划(quadratic programming,QP)问题经常出现在各种科学和工程领域,如图像处理[1]、机器人轨迹规划[2-4]、信号处理[5]和计算机视觉[6]。由于二次规划问题在现实中具有许多潜在应用的前景,因此进行实际问题研究是很有必要的。其中,时变二次规划(time-varying quadratic programming,TVQP)问题因其解决的难度大和应用的广泛性,近年来引起了越来越多研究者的关注。在大多数传统的QP问题求解方法中,例如牛顿数值迭代法[7]及其改进方法[8],通常仅适用于解决静态QP问题,在求解TVQP问题时往往会面临计算时间长和效率低的问题。
在过去几十年里,周期神经网络[9](recurrent neural network,RNN)因其并行结构而被广泛研究。梯度神经网络(gradient neural network,GNN)属于RNN,文献[10]中提出了一种基于梯度神经网络的模型,并从理论上证明了GNN解决线性矩阵方程问题的可行性。然而,在处理TVQP问题时,GNN总是会产生无法消除的残差,这表明GNN在应对时变问题方面存在局限性。为了有效地求解TVQP问题,Zhang等[11]提出了一种归零神经网络(zeroing neural network,ZNN)。与GNN不同,ZNN方法是基于实际问题构建误差函数,并通过计算误差函数对时间的导数,确保误差的每个分量在理论上都逐渐收敛为0。
近年来,ZNN模型引起了许多研究者的关注,针对不同的时变问题,提出了许多改进的ZNN模型[12-13]。总体而言,有两种方法可以提高模型的收敛性能:一种是设计新的激活函数[14]; 另一种是设计新的收敛参数。Li等[15]为了求解时变西尔维斯特方程,在ZNN模型中引入了双幂(sign-bi-power,SBP)激活函数,首次实现了模型的有限时间收敛。与激活函数一样,收敛参数在加快ZNN的收敛方面也有一定的作用。在ZNN模型中,收敛参数被设置为一个固定的常数,然而选取一个合适的固定参数取决于试验者的经验。因此,Xiao等[16]提出了一种时变参数归零神经网络(time-varying parameters zeroing neural network,TVPZNN)模型,该模型可以实现有限时间的收敛性。
然而,时变参数会随着时间的增大而增大,这将导致计算资源的浪费。为了解决模型中收敛参数过大而导致的资源浪费问题,本研究提出了一种自适应参数归零神经网络(adaptive parameter zeroing neural network,APZNN)模型。本模型引入一种基于误差的自适应收敛参数,可以根据误差的值来调节收敛参数的大小,从而避免了因参数过大而导致的计算阻塞,且模型可以在一个预设时间内收敛。与现有的变参数ZNN模型相比,APZNN有着更快的收敛速度,且收敛时间不受系统初始状态的影响。理论分析也证明了APZNN模型的稳定性、收敛性和鲁棒性。最后,通过两个仿真试验来验证了APZNN模型求解TVQP问题的可行性。
1 问题描述在数学理论中,时变二次规划(TVQP)问题的一般形式如下:
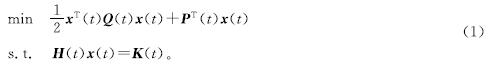
式(1)中:Q(t)∈Rn×n为时变正定黑森矩阵; P(t)∈Rn为系数向量; H(t)∈Rm×n为全秩系数矩阵; K(t)∈Rm为全秩系数矩阵。假设Q(t)、P(t)、H(t)、K(t)及它们的导数信息已知或可以估计。x(t)为式(1)的变量,目标是找到满足TVQP的理论解x*(t)。
为了求解TVQP问题,在拉格朗日乘子法[17]的基础上,设计了TVQP问题的拉格朗日函数
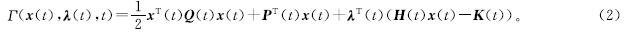
式(2)中:λ(t)∈Rm为拉格朗日乘子向量。
为了得到式(2)的最优解,Γ(x(t),λ(t),t)对x(t)和λ(t)的导数必须满足以下两个等式:
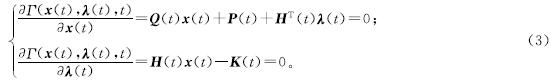
因此,上述等式可以重新表达为以下线性矩阵方程:
A(t)y(t)=B(t)。 (4)
式(4)中:
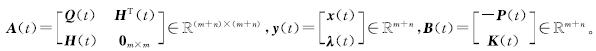
为了求解式(4),定义误差函数
E(t)=A(t)y(t)-B(t)。 (5)
然后,ZNN的设计公式表达为
(·overE)(t)=-σ Φ(E(t))。 (6)
式(6)中:σ>0为一个收敛参数,用于调整ZNN模型的收敛速度; Φ(·):Rm×n→Rm×n为激活函数,通常这个激活函数是一个单调递增的奇函数。
式(6)中的σ是一个固定的值,在实际选择过程中需谨慎考虑这一因素:选择过小的值可能导致系统收敛速度过慢,而选择过大的值又可能会浪费计算资源。此外,有研究者指出,具有时变参数的模型比具有固定参数的模型收敛得更快。然而,时变参数会随时间的增大而不断地增大,导致计算资源的消耗增加。因此,将基于误差的自适应参数引入ZNN(APZNN)模型,该参数可以根据收敛过程中误差变化情况进行自适应的调整。其设计公式如下:
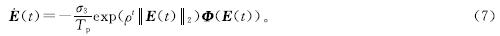
式(7)中:σ3=1/(r2(j-1))+1/(r1(1-k)); r1>0,r2>0,ρ>0; j>1; 0<k<1; Tp>0为一个预设收敛时间参数; ||·||2为二范数。增强符号双幂(enhanced sign-bi-power,ESBP)激活函数的表达式如下:
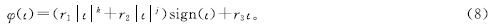
式(8)中:r1、r2、j、k的定义与之前相同; r3>0; φ(·)为Φ(·)中的一个元素。符号sign(ι)的定义如下:
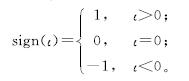
结合式(5)、式(7)和式(8),可以得到APZNN模型为
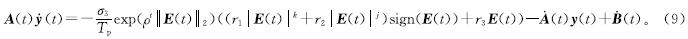
定理1 假设给出了光滑时变矩阵A(t)∈R(m+n)×(m+n)和光滑时变向量B(t)∈Rm+n,并且式(4)具有唯一解。对于任何初始向量y(0)∈Rm+n,APZNN模型(式(9))在李雅普诺夫意义上是渐进收敛的,状态解y(t)∈Rm+n收敛于理论解y*(t)∈Rm+n。
证明:由式(5)导出,APZNN模型可转化为式(7)。为了便于分析,考虑它的第i个子系统得到了如下数学形式:
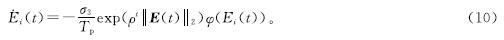
式(10)中:i∈{1,2,…,m+n}。构造一个李雅普诺夫函数
Li(t)=E2i(t)。 (11)
然后,同时取式(11)两边的时间导数:
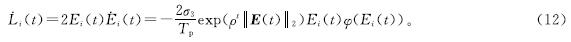
式(12)中:2σ3/Tp>0; ρt||E(t)||2≥0,所以exp(ρt||E(t)||2≥0)≥1。φ(·)是单调递增奇函数,因此它满足以下性质:

因此,李雅普诺夫函数(式(12))的关系可以很容易地表示为
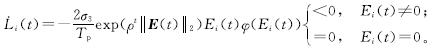
当Ei(t)=0时,系统已经趋于临界状态,因此不用讨论系统的稳定性。根据上述式子可以得到(·overL)i(t)<0总是成立的。根据李雅普诺夫稳定性定理,可以推断出APZNN模型的子系统是稳定的,即李雅普诺夫意义上的APZNN模型是渐进收敛的,状态解y(t)将收敛于理论解y*(t)。
3.2 收敛性分析定理2 假设给出了光滑时变矩阵A(t)∈R(m+n)×(m+n)和光滑时变向量B(t)∈Rm+n,并且式(4)具有唯一解,则APZNN模型的||E(t)||2最终会在预设时间Tp内收敛到0。
证明:结合式(8)和式(12),可以得到以下公式:
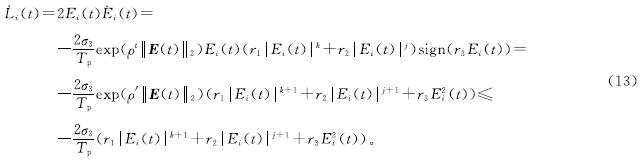
为了便于证明,假设初始值|Ei(0)|>1。因此APZNN模型的收敛过程分为两步:第一,|Ei(t)|在ta时刻从|Ei(0)|下降至1; 第二,在ta+tb时刻下降至0。具体过程如下。
1)计算第一阶段时间ta。当|Ei(t)|>1时,r1|Ei(t)|k+1+r2|Ei(t)|j+1+r3E2i(t)的大小主要由r2|Ei(t)|j+1这一项来决定。因此,式(13)可以改写为

进一步可表示为

同时对式(15)两侧取积分:
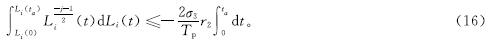
则
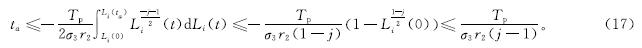
2)计算第二阶段时间tb。当0≤|Ei(t)|<1时,r1|Ei(t)|k+1+r2|Ei(t)|j+1+r3E2i(t)的大小主要由r2|Ei(t)|k+1这一项来决定。因此,式(13)可以改写为

式(18)可以被转化成:
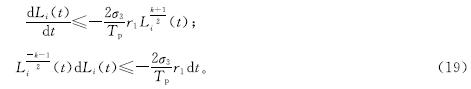
同样地,同时对式(19)两侧取积分:
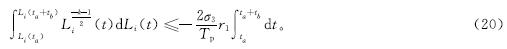
则
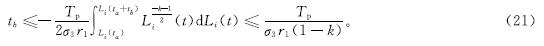
已知σ3=1/(r2(j-1))+1/(r1(1-k)),收敛时间
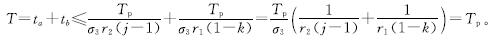
基于上述计算和分析,可以得到APZNN模型在解决式(4)时,||E(t)||2在预设时间Tp内收敛到0,同时状态解y(t)也将收敛于理论解y*(t)。
3.3 鲁棒性分析定理3 如果系统中存在时变的有界噪声Δh(t)∈Rm+n,则APZNN模型的||E(t)||2的收敛上界为 ,其中,μ为Δh(t)第i个子元素Δhi(t)的上界。
,其中,μ为Δh(t)第i个子元素Δhi(t)的上界。
证明:当系统中存在有界噪声Δh(t)时,APZNN模型可以被重新表示为
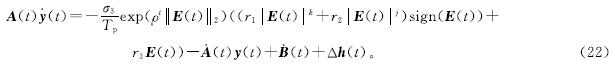
根据式(5)可以将APZNN模型转换为式(7),进一步可以推导出:
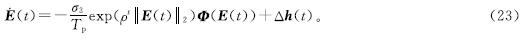
考虑式(23)的第i个子系统,则
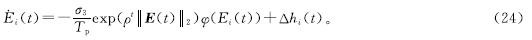
构建一个李雅普诺夫函数

取式(25)两边对时间的导数,可以推导出:
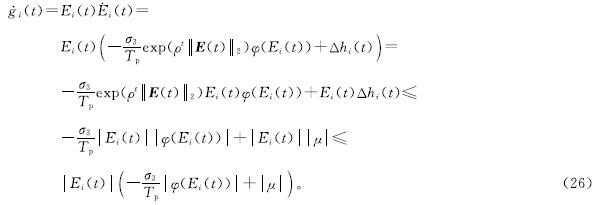
式(26)中:假设σ3|φ(Ei(t))|/Tp>|μ|,那么(·overg)i(t)<0。因为gi(t)=E2i(t)/2≥0,所以Ei(t)随着时间的增加而减少。当时间趋于无穷时,σ3|φ(Ei(t))|/Tp≤|μ|,进一步可以得到:

根据式(8)可知|φ(ι)|≥|r3ι|,那么|φ-1(ι)|≤|ι/r3|,故式(27)可以被转化为

误差范数||E(t)||2的上界为

为了说明APZNN模型的优越性,引入ZNN模型和TVPZNN模型进行比较,具体见表1。
TVQP问题(式(1))的数值例子如下:
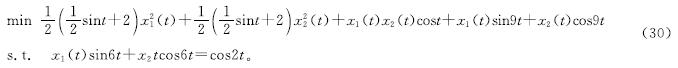
根据本文第一章的拉格朗日乘子法,将式(30)转换为线性矩阵方程:A(t)y(t)=B(t)。其中,y(t)=[x1(t),x2(t),λ(t)]T,A(t)、B(t)的具体值如下:
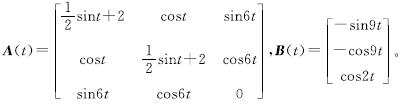
在仿真试验中,所有模型中的y(t)的初始值y(0)=[-1; 0.5; -0.5]。各个模型中的参数分别设置为:σ1=σ2=3; δ=1; δ0=0; ρ=2; r1=r2=r3=1; k=0.6; j=3。APZNN模型中的预定义收敛时间参数Tp设置为0.5 s。以下图中出现的=E(t)=2均表示误差函数E(t)=A(t)y(t)-B(t)的二范数。
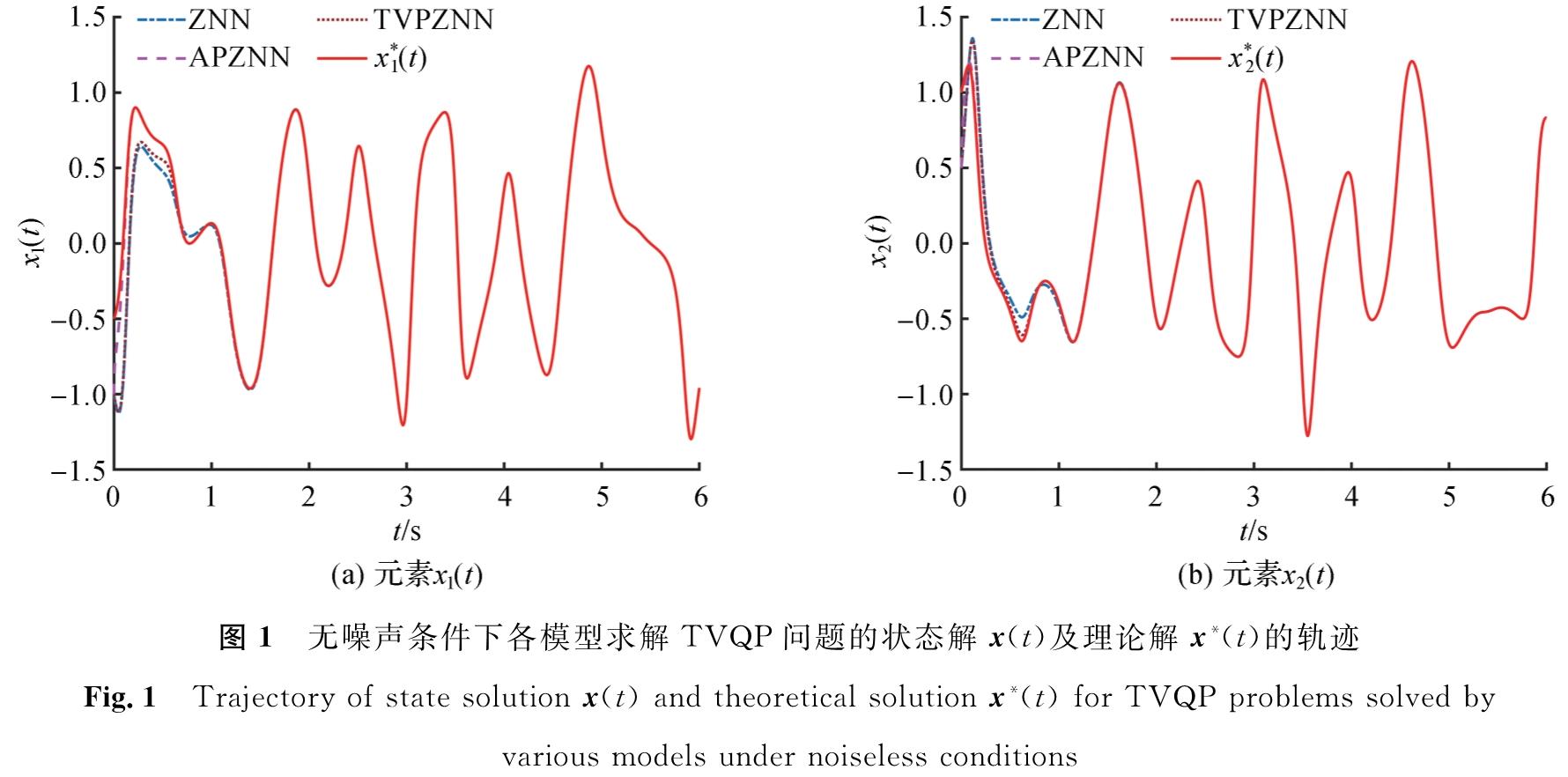
图1展示了无噪声条件下各模型求解TVQP问题的状态解x(t)及理论解x*(t)的轨迹。从图1中可以看出APZNN模型的状态解能快速地收敛到理论解,是几个模型中最快的。
图1 无噪声条件下各模型求解TVQP问题的状态解x(t)及理论解x*(t)的轨迹
Fig.1 Trajectory of state solution x(t)and theoretical solution x*(t)for TVQP problems solved by various models under noiseless conditions
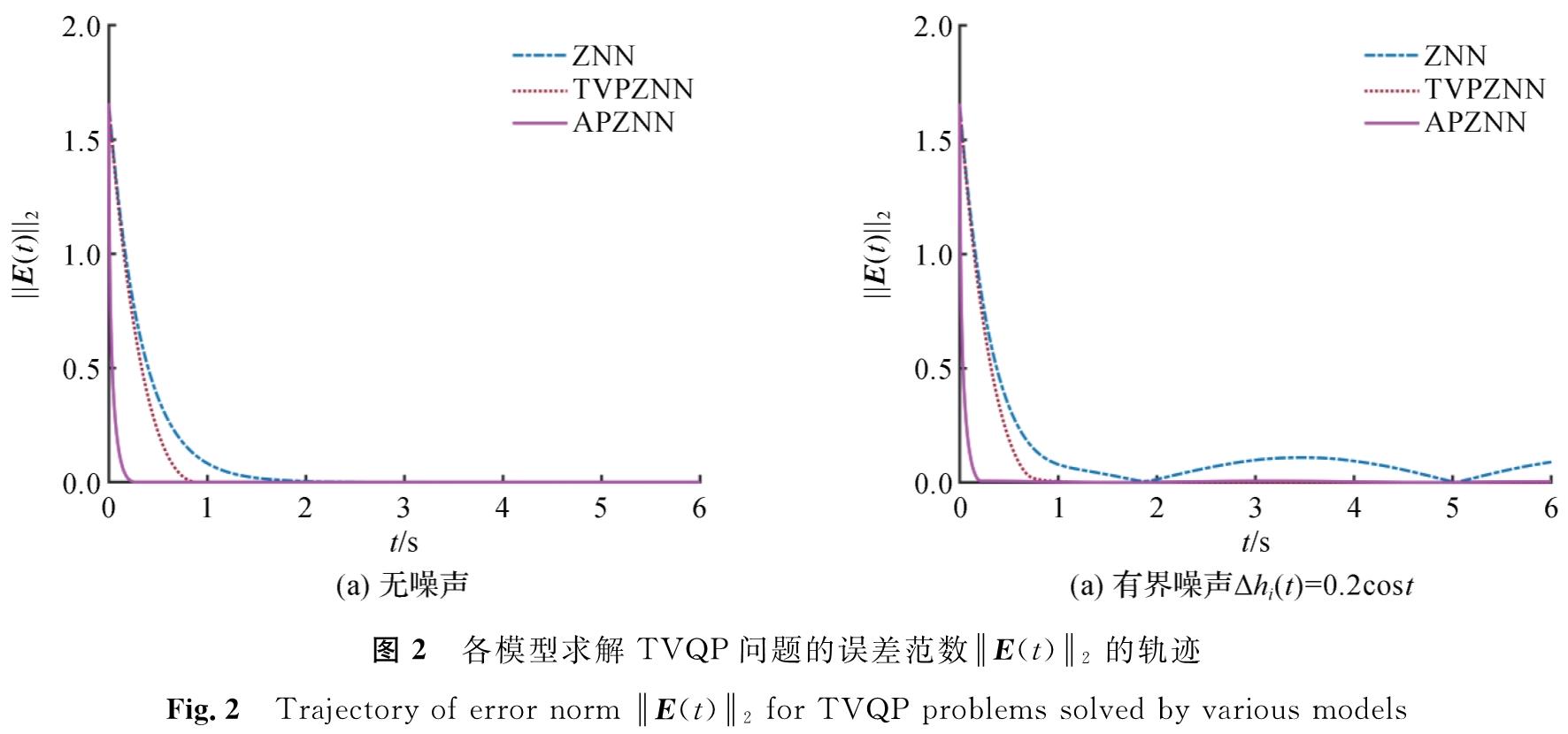
图2展示了各模型求解TVQP问题的误差范数=E(t)=2的轨迹。通过观察图2(a)可知,在理想状态下,APZNN模型的误差在0.2 s左右时可以收敛到0,小于Tp的值。由于在理论证明过程中使用了缩放的方法,因此实际的收敛时间会短于Tp,这是合理的。从图2(b)可以看出:存在有界噪声Δhi(t)=0.2cost的情况下,APZNN模型有着很强的抗噪能力,能在最短时间内收敛; 而ZNN模型则受到了很大程度的影响,误差存在一定的波动。从图2误差曲线的变化情况可以明显看出,APZNN模型的鲁棒性最强。
图2 各模型求解TVQP问题的误差范数=E(t)=2的轨迹
Fig.2 Trajectory of error norm =E(t)=2 for TVQP problems solved by various models
图3展示了不同Tp和不同初始值x(0)下APZNN模型的误差范数=E(t)=2的轨迹。从图3(a)中可以看出; 当预设时间Tp取不同值时,APZNN模型的误差总能在Tp之内收敛到0; 当Tp取0.2 s时,模型有着最快的收敛速度。图3(b)表明,对于3个不同的初始值x(0),APZNN模型有着相同的收敛速度,并且收敛时间都小于Tp。从图3可以看出,Tp。从图3可以看出,b>p可以预先设置模型的收敛时间上界,且收敛时间不受初始状态影响。
图3 不同Tp和不同初始值x(0)下APZNN模型的误差范数=E(t)=2的轨迹
Fig.3 Trajectory of error norm =E(t)=2 of APZNN model under different Tp and different initial value x(0)
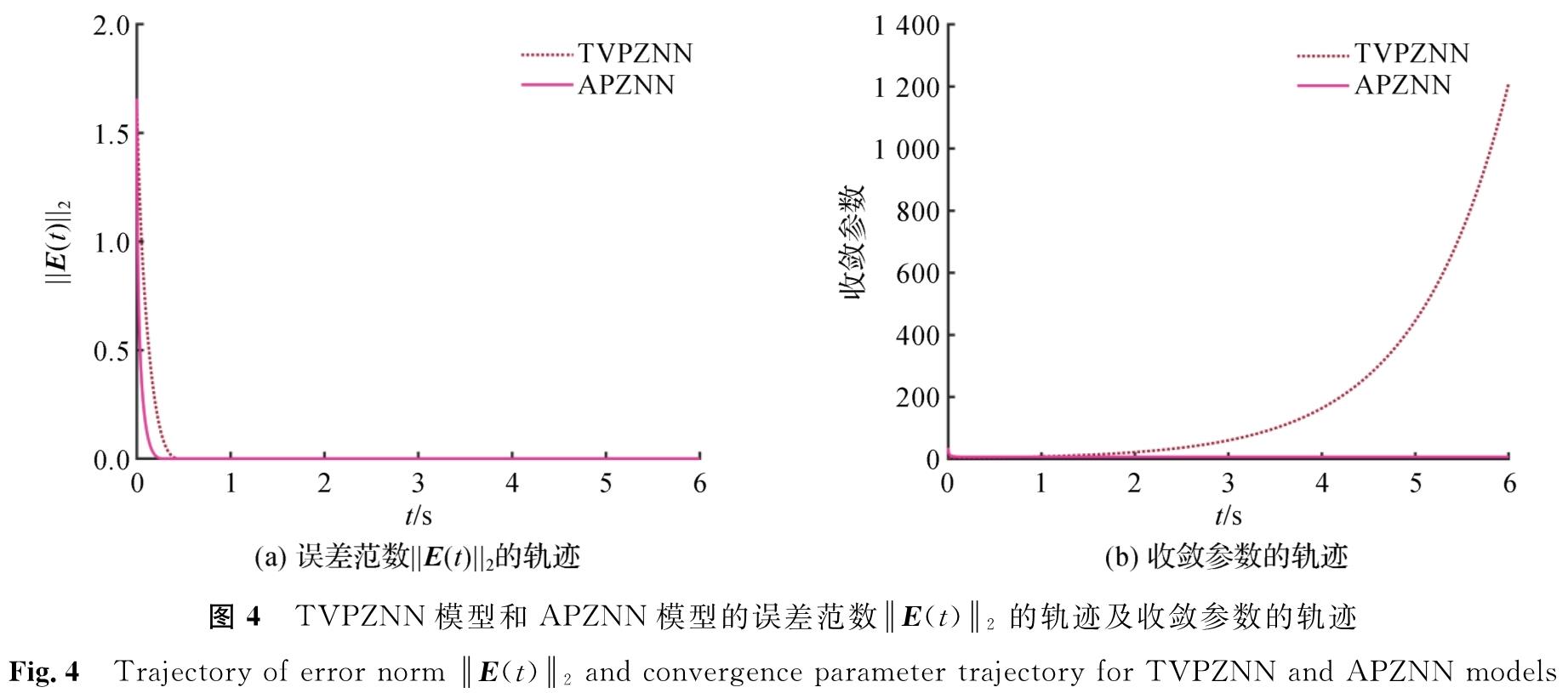
为了更好地展示APZNN模型中基于误差的自适应收敛参数的优越性,我们将激活函数(式(8))应用到TVPZNN模型中,以便于接下来的对比。图4展示了TVPZNN模型和APZNN模型的误差范数=E(t)=2的轨迹及收敛参数的轨迹。由图4(a)可知,APZNN模型在预设时间内收敛,收敛时间小于TVPZNN模型。由图4(b)可知,TVPZNN模型的收敛参数随时间的增加而增加,在6 s时TVPZNN模型的收敛参数的值达到了1 200,这大大增加了计算负担。而APZNN模型的收敛参数在刚开始时处于一个较大的值,随着模型误差的收敛,慢慢地趋于一个较小的常值,这有利于减少资源的浪费。为了进一步推断TVPZNN模型和APZNN模型的计算资源的消耗,比较了它们在求解TVQP问题时的实际计算时间(表2)。从表2中可以看出,APZNN模型比TVPZNN模型的计算速度更快,当求解的问题更复杂时,这个差距会更大。
图4 TVPZNN模型和APZNN模型的误差范数=E(t)=2的轨迹及收敛参数的轨迹
Fig.4 Trajectory of error norm =E(t)=2 and convergence parameter trajectory for TVPZNN and APZNN models
4.2 UR5机械臂路径跟踪
应用APZNN模型解决使用UR5机械臂跟踪四叶草路径的运动规划问题。在文献[18]中,一个基于TVQP的冗余机械臂重复运动规划方案被描述为
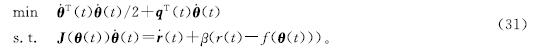
式(31)中:θ(t)∈R6,(·overθ)(t)∈R6分别为UR5机械臂的关节角度和关节角速度; q(t)=υ(θ(t)-θ(0)),υ>0为增益参数; f(·):R6→R3为非线性映射函数; 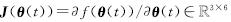 为雅可比矩阵; r(t)∈R3为末端执行器的期望路径向量;(·overr)(t)∈R3为末端执行器的期望速度向量; β>0为一个用于缩放位置反馈的常数参数。根据本文第一章的拉格朗日乘子法将式(31)转换为线性矩阵方程:A(t)y(t)=B(t),矩阵和向量的定义分别如下:
为雅可比矩阵; r(t)∈R3为末端执行器的期望路径向量;(·overr)(t)∈R3为末端执行器的期望速度向量; β>0为一个用于缩放位置反馈的常数参数。根据本文第一章的拉格朗日乘子法将式(31)转换为线性矩阵方程:A(t)y(t)=B(t),矩阵和向量的定义分别如下:
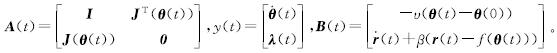
本仿真试验使用基于APZNN模型的逆运动学控制方法来控制UR5机械臂,以跟踪三维空间中的四叶草路径。APZNN模型中的参数与上述数值仿真试验中相同; υ=β=1; UR5机械臂的初始关节角度向量为θ(0)=[0,-π/2,-π/2,-π/3,π/2,0]T。
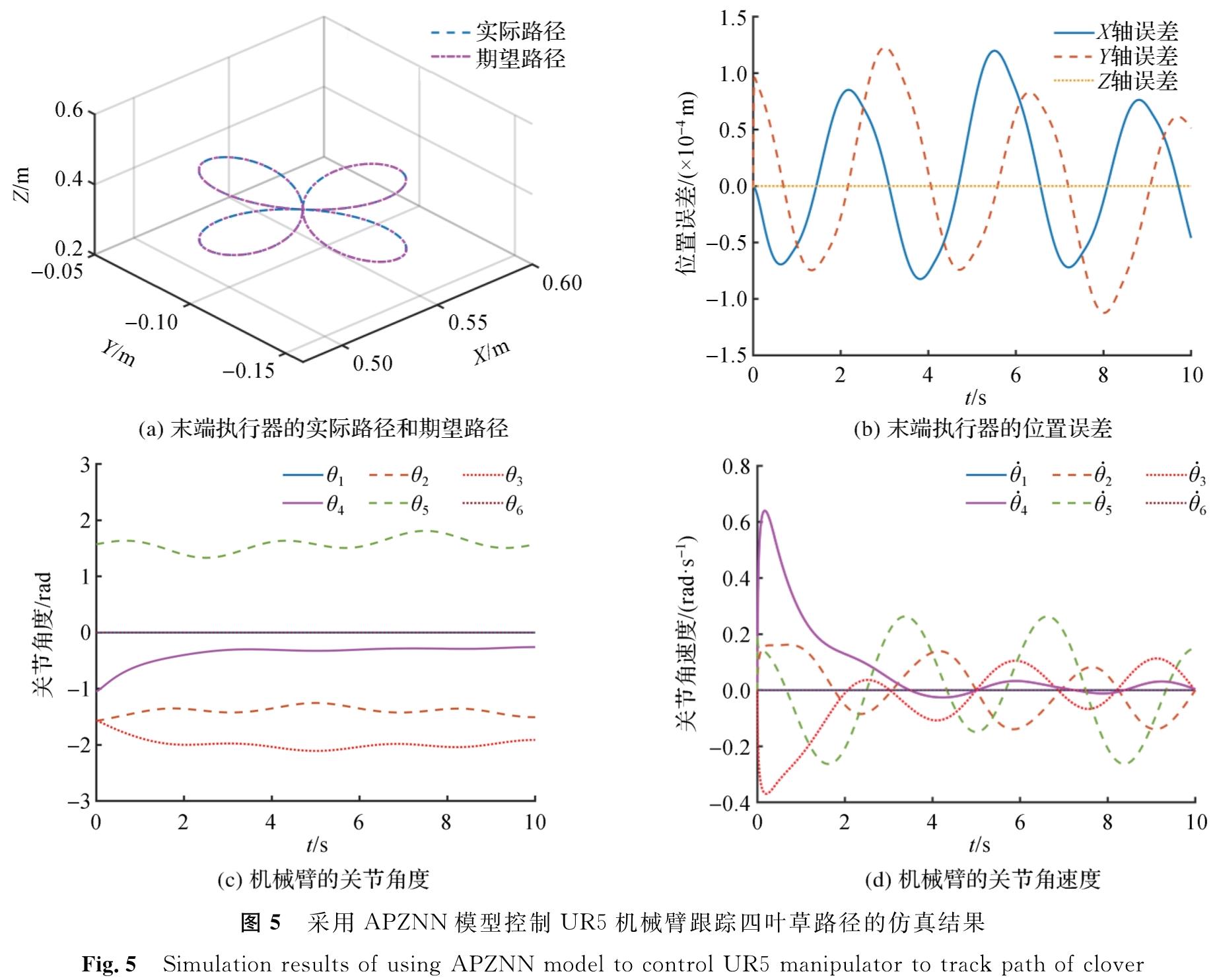
采用APZNN模型控制UR5机械臂跟踪四叶草路径的仿真结果如图5所示。图5(a)为机械臂的末端执行器的期望路径和实际路径的轨迹,从中可以看出,末端执行器可以很好地跟踪期望的路径。末端执行器对应的3个方向上的位置误差如图5(b)所示,3个方向上的位置误差都被限制在-1.5×10-4 m和1.5×10-4 m之间,这也验证了本研究提出的APZNN模型的有效性。图5(c)和图5(d)分别展示了关节角度和关节角速度的变化曲线,从中可以看出变化曲线平滑,说明控制的过程相对稳定。
图5 采用APZNN模型控制UR5机械臂跟踪四叶草路径的仿真结果
Fig.5 Simulation results of using APZNN model to control UR5 manipulator to track path of clover
5 结 语
本研究提出了一种求解TVQP问题的APZNN模型,引入了一个基于误差的自适应收敛参数,有效地解决了时变收敛参数过大的问题,且APZNN模型具有预设时间的收敛性。此外,理论分析还证明了APZNN模型的稳定性,预设时间收敛性和鲁棒性。同时,仿真试验结果表明,APZNN模型比ZNN模型和TVPZNN模型有着更优越的收敛性和更强的鲁棒性。最后,将APZNN模型应用于UR5机械臂的路径跟踪问题,其结果表明APZNN模型在解决工程实际问题中的有效性。本仿真试验的机械臂路径跟踪是基于MatLab平台的框架搭建,在未来,考虑将APZNN模型应用于真实的机械臂路径跟踪中。
- [1] HU Z, XIAO L, DAI J H, et al. A unified predefined-time convergent and robust ZNN model for constrained quadratic programming[J]. IEEE Transactions on Industrial Informatics,2021,17(3):1998.
- [2] 孔颖,吴佳佳,雷景生,等.基于有限时间对偶神经网络的冗余机械臂重复运动规划[J].控制理论与应用,2023,40(1):139.
- [3] 金龙,张凡,刘佰阳,等.基于数据驱动的冗余机器人末端执行器位姿控制方案[J].自动化学报,2024,50(3):518.
- [4] 陈思远.基于神经动力学的冗余度机器人混合优化策略[D].广州:华南理工大学,2022.
- [5] MATTINGLEY J, BOYD S. Real-time convex optimization in signal processing[J]. IEEE Signal Processing Magazine,2010,27(3):50.
- [6] WANG P, SHEN C H, HENGEL A V D, et al. Large-scale binary quadratic optimization using semidefinite relaxation and applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2017,39(3):470.
- [7] XU H K. An iterative approach to quadratic optimization[J]. Journal of Optimization Theory and Applications,2003,116(3):659.
- [8] GUO D S, ZHANG Y N. Neural dynamics and Newton-Raphson iteration for nonlinear optimization[J]. Journal of Computational and Nonlinear Dynamics,2014,9(2):021016.
- [9] FENG J Q, QIN S, SHI F L, et al. A recurrent neural network with finite-time convergence for convex quadratic bilevel programming problems[J]. Neural Computing and Applications,2018,30(11):3399.
- [10] GUO D S, YI C F, ZHANG Y N. Zhang neural network versus gradient based neural network for time-varying linear matrix equation solving[J]. Neurocomputing,2011,74(17):3708.
- [11] LIAO B L, ZHANG Y N. Different complex ZFs leading to different complex ZNN models for time-varying complex generalized inverse matrices[J]. IEEE Transactions on Neural Networks and Learning Systems,2014,25(9):1621.
- [12] ZHANG Z J, ZHENG L N, QIU T R, et al. Varying-parameter convergent-differential neural solution to time-varying overdetermined system of linear equations[J]. IEEE Transactions on Automatic Control,2020,65(2):874.
- [13] JIN J, ZHAO L, LI M, et al. Improved zeroing neural networks for finite time solving nonlinear equations[J]. Neural Computing and Applications,2020,32:4151.
- [14] SUN M X, LI X, ZHONG G M. Performance enhancing ZNN models for time-variant equality-constraint convex optimization solving:a transition-state based attracting system approach[J]. Expert Systems with Applications,2024,237:121559.
- [15] LI S, CHEN S F, LIU B. Accelerating a recurrent neural network to finite-time convergence for solving time-varying Sylvester equation by using a sign-bi-power activation function[J]. Neural Processing Letters,2013,37(2):189.
- [16] XIAO L, HE Y J, LIAO B L. A parameter-changing zeroing neural network for solving linear equations with superior fixed-time convergence[J]. Expert Systems with Applications,2022,208:118086.
- [17] JIN J, CHEN W J, CHEN C Y, et al. A predefined fixed-time convergence ZNN and its applications to time-varying quadratic programming solving and dual-arm manipulator cooperative trajectory tracking[J]. IEEE Transactions on Industrial Informatics,2023,19(8):8691.
- [18] ZHENG L N, ZHANG Z J. Time-varying quadratic-programming-based error redefinition neural network control and its application to mobile redundant manipulators[J]. IEEE Transactions on Automatic Control,2022,67(11):6151.
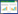 图 1 无噪声条件下各模型求解TVQP问题的状态解x(t)及理论解x*(t)的轨迹
Fig.1 Trajectory of state solution x(t)and theoretical solution x*(t)for TVQP problems solved by various models under noiseless conditions
图 1 无噪声条件下各模型求解TVQP问题的状态解x(t)及理论解x*(t)的轨迹
Fig.1 Trajectory of state solution x(t)and theoretical solution x*(t)for TVQP problems solved by various models under noiseless conditions