共识算法已成为区块链技术向数字金融、车联网等领域深层渗透研究的热点和难点[1]。实用拜占庭容错算法(practical Byzantine fault-tolerant algorithm,PBFT)由Miguel和Barbara首次提出,因其启动节点数量少、共识效率和容错率高而在私有链和联盟链中得到大量应用[2]。PBFT是一种基于状态机复制的共识算法,在分布式系统的不同节点中进行副本复制,每个状态机的副本都保存了服务的状态和所实现的操作,其原理是让每个收到消息的节点都去询问其他节点收到的消息内容,在发生错误的节点比例不超过节点总数1/3的情况下仍可保证系统正常运行[3]。
人们对PBFT进行了大量的研究。He等[4]提出平均主义实用拜占庭容错算法,优化PBFT中选择主节点的过程,从而使链中的每个节点都是平等且高效的,提高了数据备份和验证的效率,优化了区块链的共识过程。Gueta等[5]为区块链提出了一种可扩展的分散信任基础设施,解决了可扩展性和分散性两大挑战,同时支持Ethereum[6]和智能合约[7]的执行。Li等[8]针对PBFT不适合动态网络的问题提出改进的可扩展PBFT算法,可以根据系统的网络环境采取不同的步骤来达成共识,该算法使用可验证随机函数来选择共识节点,简化节点协议和视图更改协议,以减少通信开销和共识所需时间。涂园超等[9]提出基于信誉投票的PBFT改进方案,根据节点划分评估机制动态地选取可靠节点参与共识,并根据节点状态转移机制转换节点的角色,提高了系统共识的安全性与稳定性。唐宏等[10]在PBFT中引入节点基础配置评分及信誉评分机制,依据信誉评分机制计算节点可靠性,并根据节点可靠性来选取领导节点与共识节点,以减少参与共识的节点数。上述研究均基于共识流程的优化与节点数量的调整,因此PBFT算法仍存在随节点数增加,系统共识时延增大、吞吐量下降,同时通信复杂度呈平方级增长的问题。对此,本研究提出一种基于节点间通信时延分组的实用拜占庭容错算法(grouping PBFT,GPBFT)。通过将节点间通信时延较小的节点进行分组,从而在减少共识节点数量的基础上降低共识时延、提升吞吐量并降低通信复杂度的数量级; 同时设计节点信誉评分机制,有效降低恶意节点参与共识过程的概率,提高系统共识的稳定性与安全性。
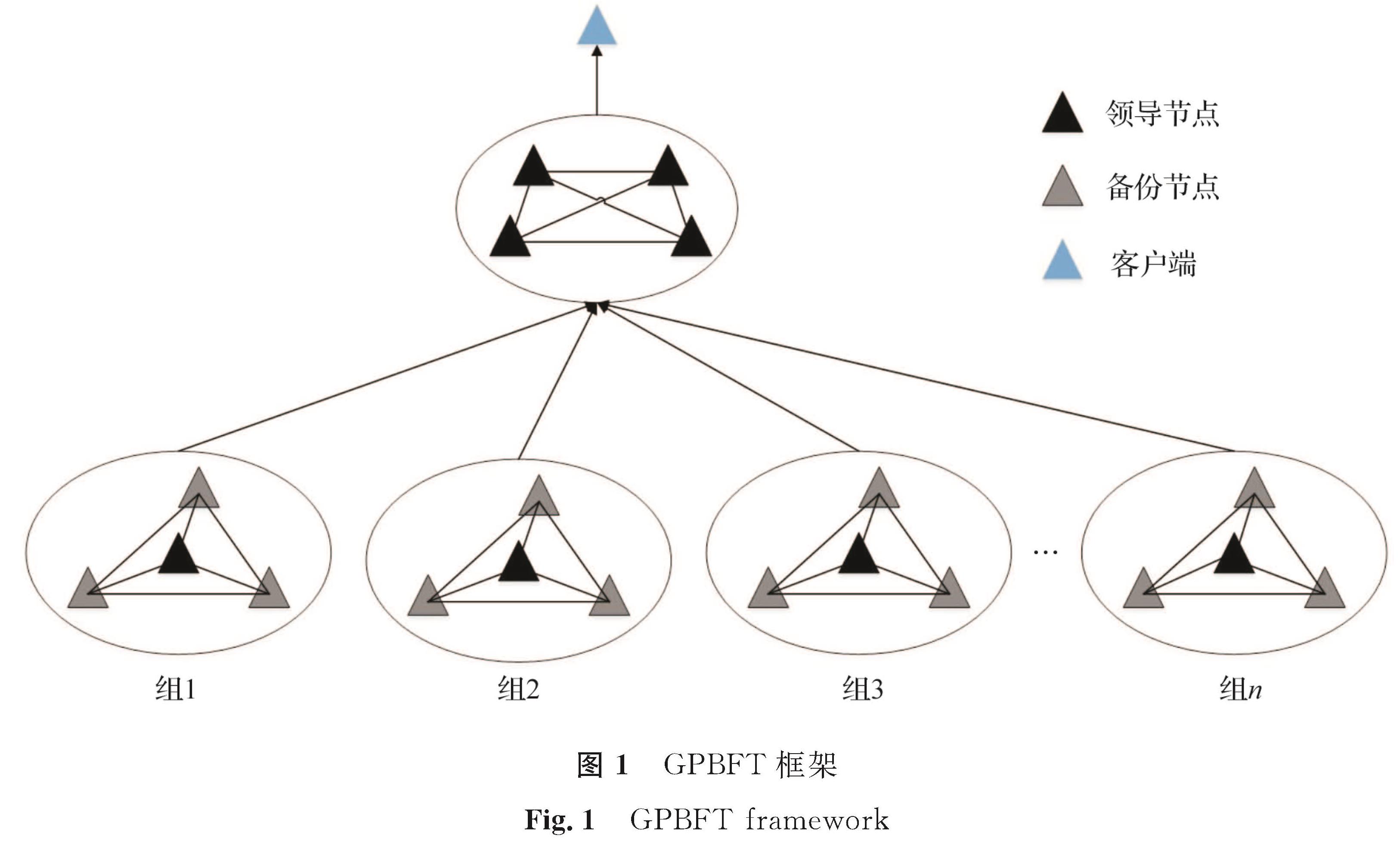
1 GPBFT概述GPBFT由领导节点(leader node,LN)、备份节点(replica node,RN)和客户端构成,GPBFT框架如图1所示。在GPBFT中,LN是小组内主节点,其作用为组内共识请求的广播与验证消息的收集; RN是参与组内共识的节点,负责接收与验证由LN和其他RN发送的消息; 客户端是共识的请求者,不参与共识的具体过程。
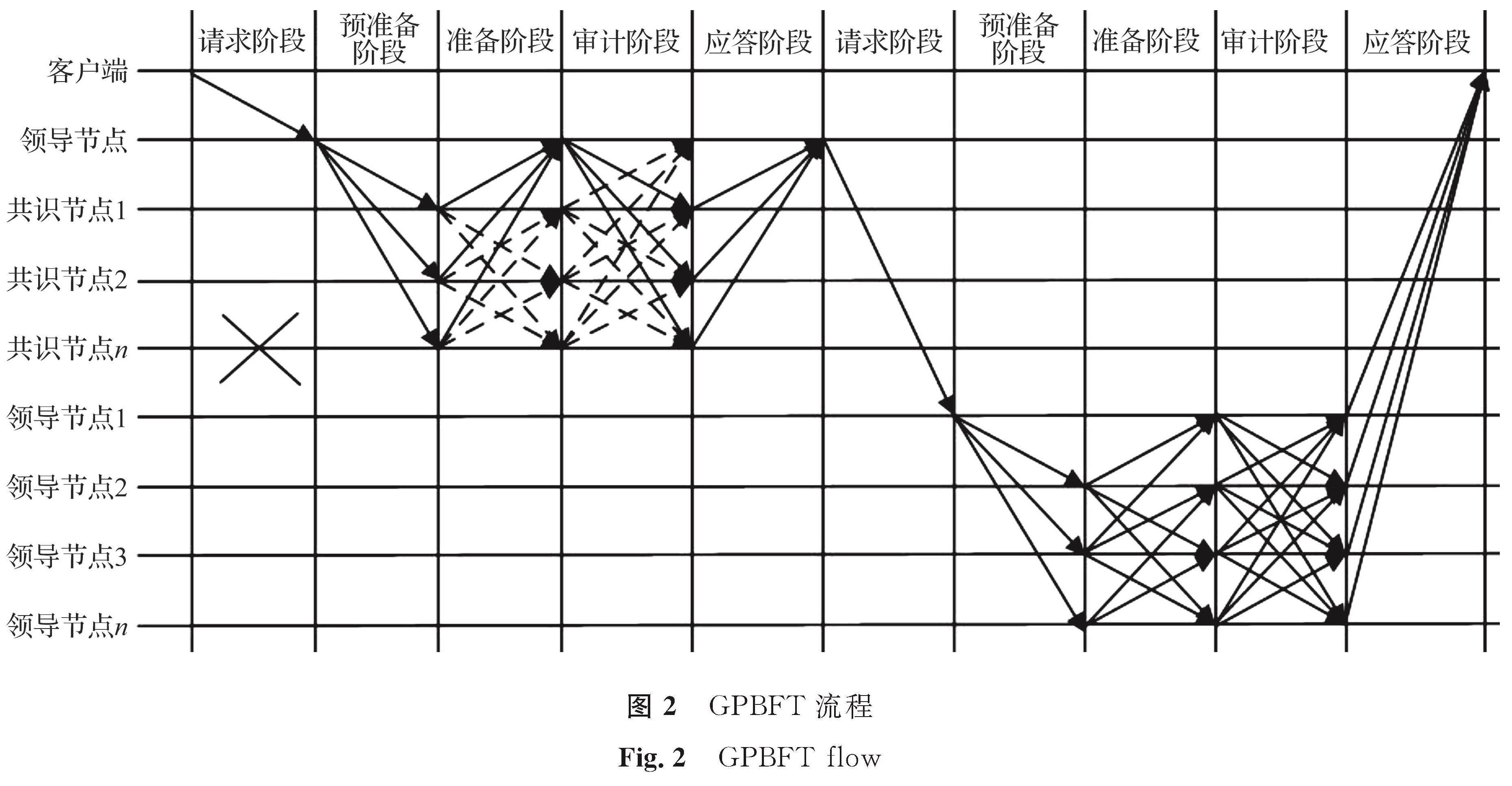
GPBFT流程如图2所示。GPBFT主要包含两部分:第一部分为组内共识,首先区块链系统提供节点集合{Z},依据最少网络通信次数原则确定分组数m,然后计算各组内节点间平均通信时延,据此选出组内低于平均时延的节点并确定各组内节点数,同时依据组内最低通信时延与节点信誉评分机制选出各组内LN,最后由组内LN与RN构成共识节点进行组内共识; 第二部分为全局LN共识,完成组内共识后,各组的LN组成LN小组,进行全局LN共识,对于产生共识请求的具体组号,则由发起共识请求的客户端位置决定。
共识流程具体如下:
1)组内请求阶段。在完成节点分组与组内LN选择后,由客户端发起共识请求,进行小组内的共识。
2)组内预准备阶段。在预准备阶段,所有组内节点都必须接收由该组LN发出的请求消息,并给每个共识节点广播事务的执行顺序。LN对需要放置在复制节点中的新区块中的多个事务进行排序,并将它们存储在列表中,然后向整个组内广播该列表。
3)组内准备阶段。各节点收到交易列表后,对交易的完整性和合法性进行验证和审计。将审计结果添加到每个节点的数字签名中,并广播给其他非LN。
4)组内审计阶段。RN接收并总结来自其他RN的审计结果,并将它们与自己的审计结果进行比较,然后向其他节点广播确认消息。
5)组内应答阶段。当LN和RN都收到一定数量的相同审计结果时,RN将其记录的审计结果反馈给组内LN。若组内共识结果在审计后无误,则由该组内的LN向其他小组的LN进行广播,申请LN共识。
6)全局LN共识。在完成组内共识后,组内LN向全局的LN发起共识,共识过程与组内共识流程一致。若存在异常节点,且异常节点f与全局节点Z之间满足f≤(Z-1)/3时,则采用少数服从多数的基本原则,不影响共识结果。达成共识后,各节点一致同意将新区块加入区块链。
GPBFT继承PBFT的基本共识流程,保留系统存在恶意节点时的容错率,因而提高了系统的安全性。GPBFT考虑到实际节点数量激增导致的高时延与节点信誉问题,对PBFT进行了如下改进:1)对系统全局节点进行分组,将PBFT的全局共识模式改进为小组内共识,从而大大减少了参与共识的节点数量,提高了共识效率; 2)将节点间通信时延较小的节点进行归类分组,从而在减少共识数量的基础上降低共识时延; 3)提出了节点信誉评分机制,依据节点信誉评分来进行LN选择,从而减小了恶意节点参与共识的概率。
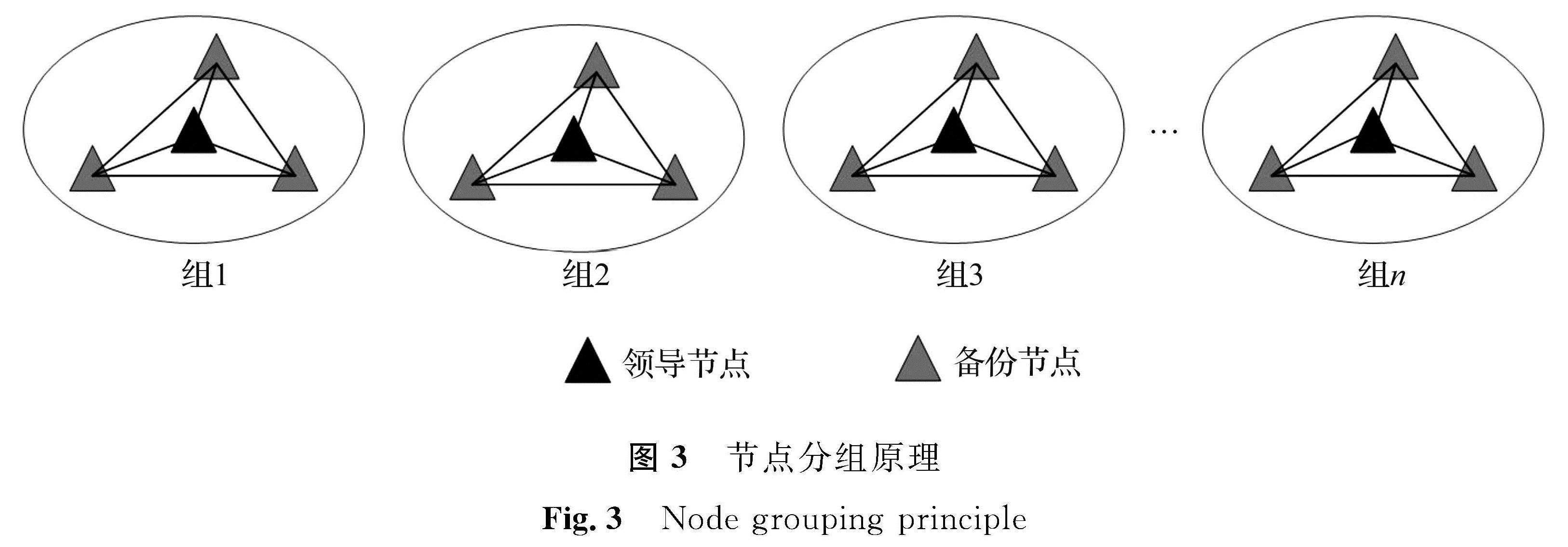
2 GPBFT实现2.1 基于节点间通信时延的节点分组算法随着实际网络与节点性能的变化,节点间通信时延情况会出现波动,影响共识效率。对此,本研究提出一种基于节点间通信时延的分组算法,通过计算节点间通信时延,将低于平均通信时延的节点归为一组,有效降低了共识过程中的通信消耗。节点分组原理如图3所示。
下面介绍分组算法具体流程。
首先,计算初始节点集合{Z}中的节点间通信时延。通信时延包括发送时延、传播时延、处理时延和排队时延[11]。在此处将上述4种时延相加作为系统节点的总时延,记为D。那么,两节点之间的时延可计算如下:
D=Dj-Di。 (1)
式(1)中:Dj为系统节点数量为n的区块链网络中节点i接收到节点j响应的时间; Di为节点i发送的请求时间。为了判断节点在系统全网中通信时延的相对大小,我们提出节点平均通信时延(-overD),计算如下:

然后,预选组内LN。由计算得到的节点平均通信时延来统计各组中通信时延最小的节点,得到组内LN。
最后,筛选组内RN。完成组内LN统计后,对小组内节点间时延进行升序排序,将通信时延大于(-overD)的节点移出组外,以保证组内节点的通信时延处于较低水平。移出组外的节点会与其他小组节点进行通信时延计算,若通信时延小于组内平均值,则加入该小组内; 若通信时延仍然大于其他小组平均值,则节点无法加入该组,该节点会与其他类似节点进行组队。
2.1.1 GPBFT网络通信次数分析假设系统节点总数Z分为m(m≥3)组,各组中有n+1(n≥3)个节点,则系统单次共识通信次数计算如下:
S1=m(n+1)2+m2。 (3)
PBFT完成一次共识,系统通信次数计算如下:
S2=2Z2-Z-1。 (4)
将GPBFT与PBFT通信次数进行比较,得
S1-S2=m(n+1)2+m2-2Z2+Z+1。
由于Z=m(n+1),得
S1-S2=(1/m-2)Z2+Z+m2+1<0。
可见,GPBFT的通信复杂度小于PBFT。
2.2.2 GPBFT网络通信最少次数计算在分析最小通信次数时,同样假设系统节点总数Z分为m(m≥3)组。将m=Z/(n+1)代入式(3),计算得
S1=Z(n+1)+(Z2)/((n+1)2)。(5)
在式(5)中对n分别进行一阶和二阶求导,得:

根据式(6)和式(7)求出极值点,即可在确保通信次数最低的情况下获得最佳小组数m与组内节点数。
2.2 节点信誉评估机制节点信誉评估机制对参与共识的节点行为进行评估,以区分高信誉值节点与恶意行为节点。首先,给刚进入系统的节点i(节点参与共识的轮数t=0)赋予初始信誉值r(i,0)=0.5; 然后,引入共识错误率fi、共识成功率si和历史行为评估参数ai。
2.2.1 共识错误率共识错误率f的设置是为了避免错误率较高的节点成为LN,该参数对节点的信誉值有负面作用,定义如下:
f=(fi)/(tfalse),f∈[0,1]。 (8)
式(5)中:fi为节点i生成有效块失败的次数; tfalse为节点生成块失败的总次数。对于新节点或从未生成块的节点,其错误率f=0。
2.2.2 共识成功率共识成功率s衡量了节点成功参与生成区块的能力,优先选择成功率较高的节点作为LN或RN,这样可以提高共识速度,定义如下:
s=(si)/(ttotal),s∈[0,1]。 (9)
式(6)中:si为节点i成功创建块的次数; ttotal为节点生成块的总数。对于新节点或从未生成块的节点,其成功率s=0。
2.2.3 历史行为评估参数历史行为评估参数ai体现节点参与共识过程中的稳定性,能判断节点加入区块链网络后的发展情况,从而促使节点做出良好的行为以维持较好的历史行为评估参数,定义如下:

式(10)中:r(i,n)为节点i在当前时刻的信誉值; r(i,t)为节点i在t时刻的信誉值。对于新节点或从未生成块的节点,其ai=0。
2.2.4 节点信誉值通过初始信誉值、错误率、成功率和历史行为评估参数来确定节点最终的信誉值R(i,t)。在信誉值的计算过程中,各项参数对总体信誉值影响的程度是不同的,本研究重点在节点错误率与成功率,以激励节点能正常运行。参考文献[12],定义各因素所占权重如下:
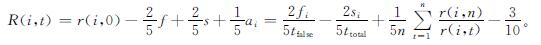
各组完成LN预选后,由信誉评分机制计算各组预选LN的信誉评分。在首次分组共识前,默认节点信誉评分R(i,0)=0.5。随着系统共识次数的增加,若节点信誉值R(i,t)<0.5,则预选LN或组内RN被禁止参与共识过程,组内LN重新选择; 当节点信誉值R(i,t)≥0.5时,预选LN成为组内主节点,RN允许参与共识。在选择LN时,若两节点的信誉值R(i,t)相同,则优先选择通信时延较小的节点。
3 试验分析3.1 试验设计为分析GPBFT的性能,分别对吞吐量、共识时延和通信复杂度进行试验分析,通过与PBFT对比试验来分析GPBFT的共识效率与稳定性,环境为Intel CoreTM i7-7700HQ,内存为16 GB。试验在区块链环境下进行,因此利用Linux系统建立基于Hyperledger Fabric1.0环境下的区块链系统,通过Python3.9.2实现了PBFT和GPBFT的运行。首先,为分析不同节点数量对GPBFT性能的影响,将模拟节点数分别定为5、10、15、20至65(每5个节点取1个),得到初始节点集合{Z}; 然后,为模拟节点的通信时延D,在得到初始节点集合后,利用随机算法得到节点集合的通信时延矩阵; 最后,在虚拟机中开启多个进程,分别测试不同节点数量情况下PBFT与GPBFT共识时间,每个进程试验20次,取平均值后统计平均共识时延与吞吐量,并分析不同场景下的系统通信复杂度。
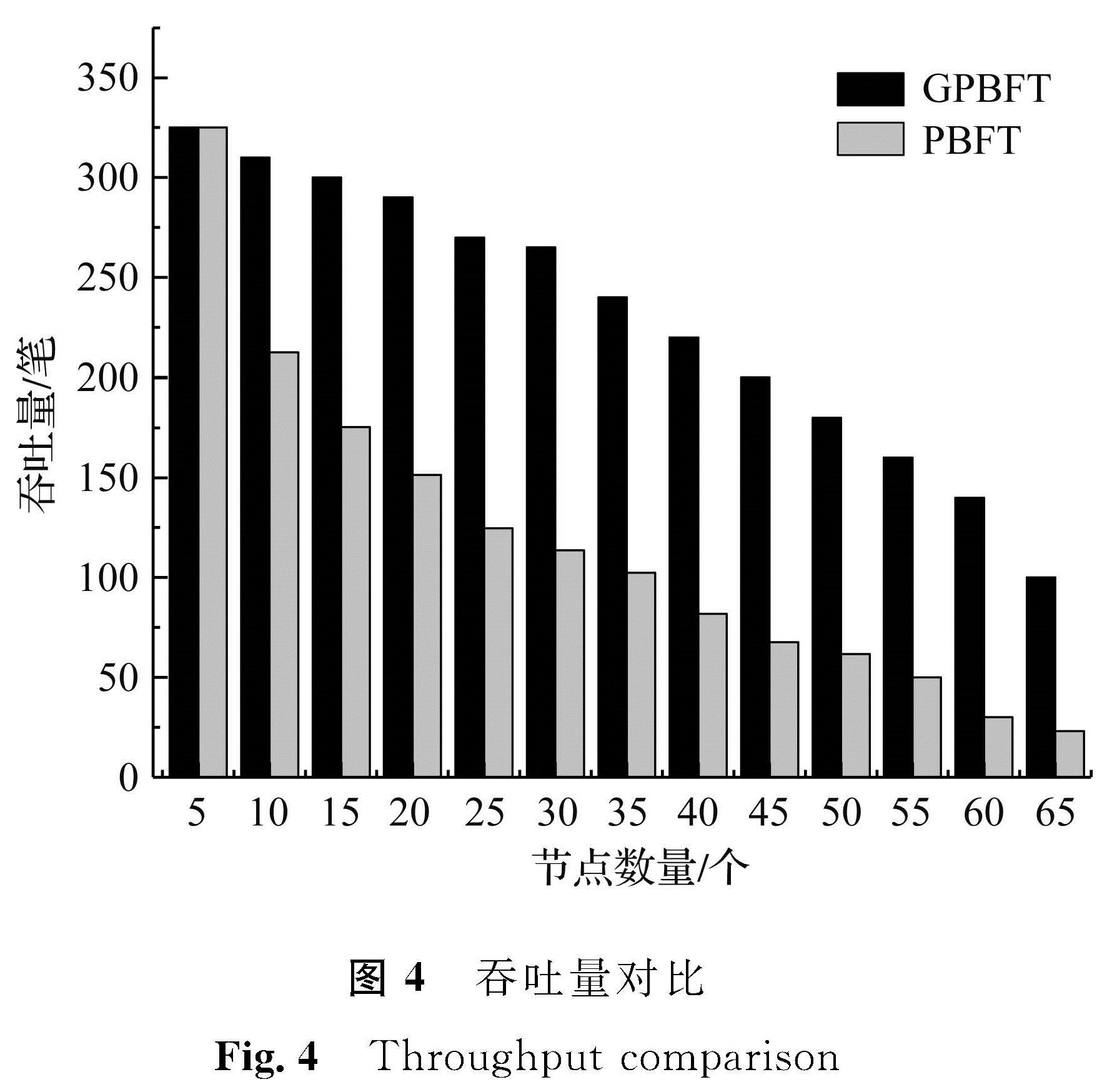
3.2 试验结果分析3.2.1 吞吐量吞吐量是衡量一致性算法性能的重要指标,表示单位时间内的交易数量。在吞吐量试验中,固定交易次数为500次,统计完成500次交易所用时间,然后计算两种算法的吞吐量,吞吐量对比如图4所示。
由图4可知,在节点数量较少时,PBFT和GPBFT两种共识算法的吞吐量都较高,随着节点数量的增加两者的吞吐量都在下降,但是PBFT的吞吐量下降速率较快,表明随着节点数量的增加,PBFT的性能下滑严重。GPBFT比PBFT平均吞吐量提高了55.04%,在节点数为35和65时,吞吐量下降速率加快,原因是在节点数量较多情况下分组算法增加了共识组数,LN共识数量的增加对共识效率产生了负影响,但吞吐量仍远高于PBFT。
3.2.2 共识时延
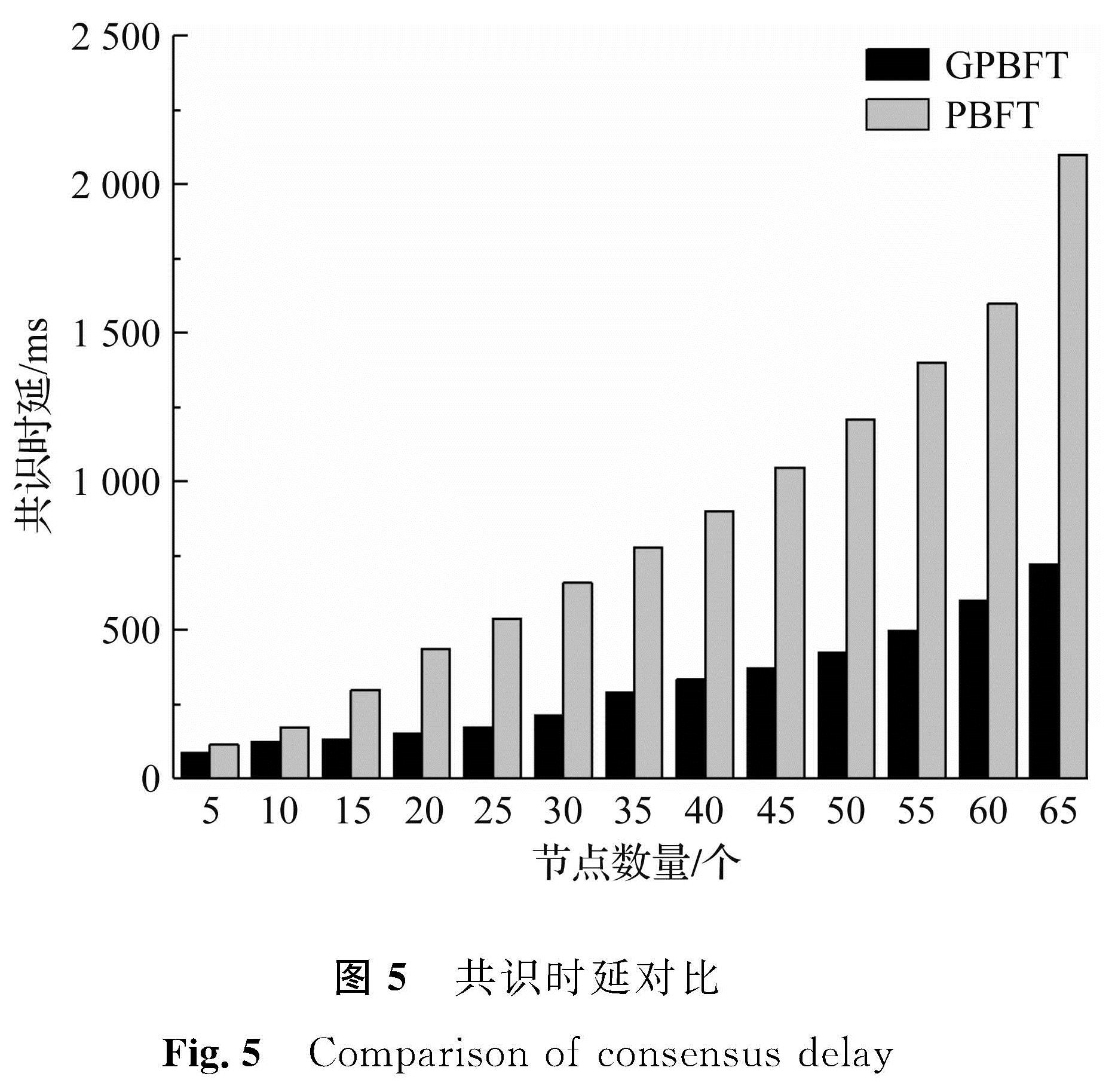
共识时延是衡量共识算法性能的关键因素之一,时延越小表示共识算法完成一轮共识所用的时间越短,共识效率更高。试验设置PBFT作为对照组,分别对两种共识算法进行20轮共识测试,统计共识时延并取平均值,共识时延对比如图5所示。
由图5可知,随着共识节点的增加,PBFT共识时延剧增,而GPBFT的共识时延增长较为平缓,GPBFT相比PBFT平均时延降低了57.86%,可见节点数量的增加对PBFT共识效率的影响远大于GPBFT。在分组算法将节点分组后,系统共识效率明显提高且系统更稳定。
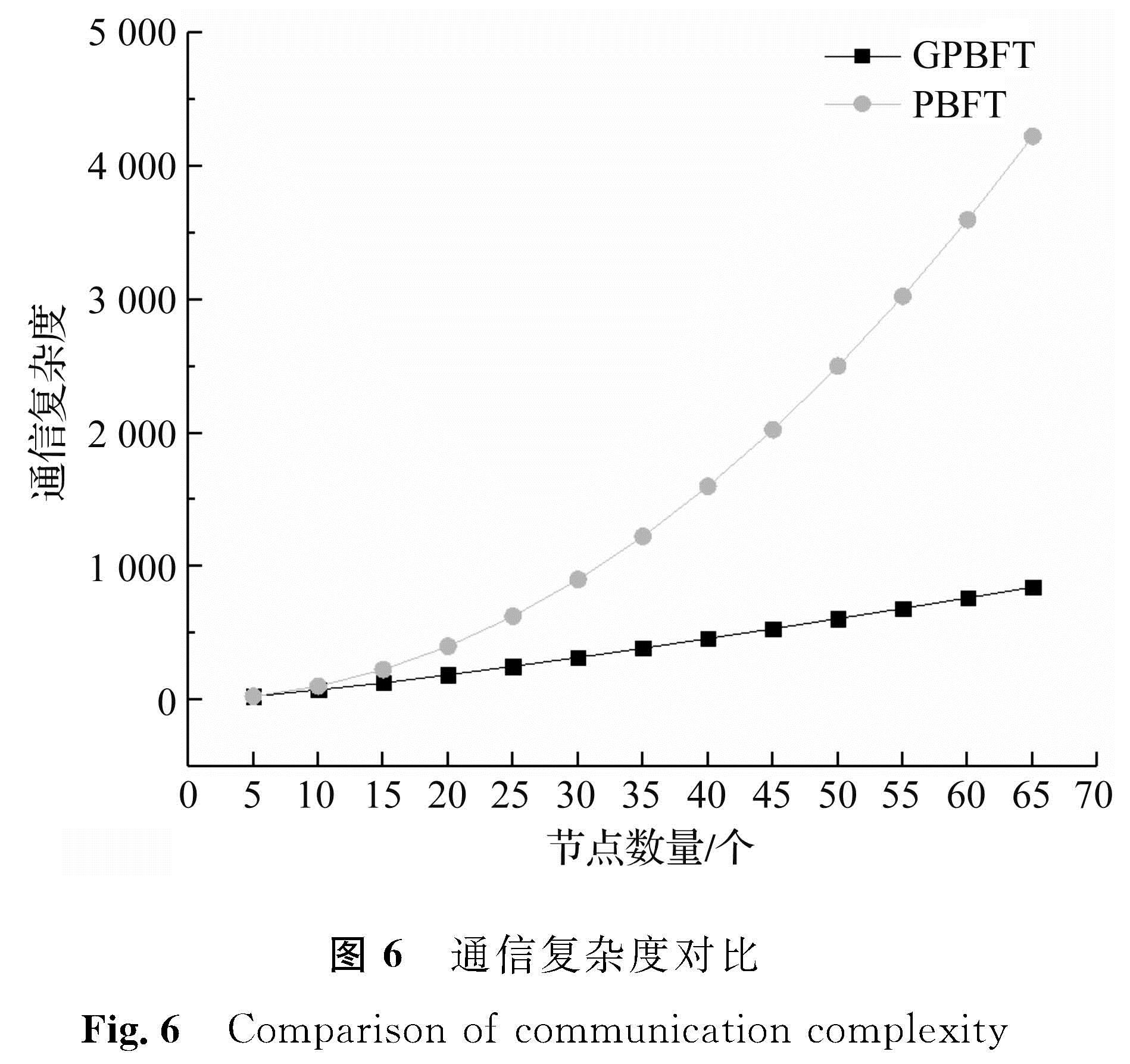
3.2.3 通信复杂度PBFT的通信复杂度已知为O(Z2),GPBFT的通信复杂度通过参考文献[13]计算而得:C=mZlogmZ。试验分别将节点总数Z与分组数m代入两种算法的通信复杂度中,通信复杂度对比如图6所示。
在节点数量较少时,GPBFT通信复杂度与PBFT较接近,随着节点数量增加,GPBFT通信复杂度则远小于PBFT,且增幅较小,通信稳定。可见在节点数量较多时,GPBFT能大幅降低系统通信复杂度,提高系统效率。
4 结 语为解决PBFT效率低下的问题,本研究提出了GPBFT。首先,基于分组算法将系统中通信时延较低的节点分成一组,以降低节点间的通信时延; 然后,选出各个小组中的LN并且建立节点监管机制,以减少LN的视图转换,从而降低算法的通信代价; 最后,通过试验对比分析发现,GPBFT相对于PBFT在共识时延、通信复杂度等方面有较大的提升,从而有效提高了系统共识效率,解决了行业区块链系统大规模节点的需求问题。
目前,GPBFT仍处于理论试验阶段。下一步,我们将继续研究GPBFT在共识节点总数不确定的情况下,如何动态控制各组中节点数量大小,以达到更好的共识效率; 并进一步研究在具体应用场景下,对不同特征进行分组后的共识效率,从而为GPBFT的实际工程应用打好理论基础。
- [1] 袁勇,周涛,周傲英,等.区块链技术:从数据智能到知识自动化[J].自动化学报,2017,43(9):1486.
- [2] CASTRO M, LISKOV B. Practical Byzantine fault tolerance[J].ACM Transactions on Computer Systems,2002,20(4):398.
- [3] NGUYEN G T, KIM K. A survey about consensus algorithms used inblockchain[J].Journal of Information Processing Systems,2018,14(1):101.
- [4] HE L, HOU Z. An improvement of consensus fault tolerant algorithm applied to alliance chain[C]//IEEE 9th International Conference on Electronics Information and Emergency Communication. Beijing: IEEE,2019:1.
- [5] GUETA G G, ABRAHAM I, GROSSMAN S, et al. SBFT: a scalable decentralized trust infrastructure for blockchains[EB/OL].(2018-04-04)[2022-01-28].
- [6] TOYODA K, MACHI K. Function-level bottleneck analysis of private proof-of-authority ethereum blockchain[J].IEEE Access,2020(8):141611.
- [7] BATAINEH A S, BENTAHER J. Specifying and verifying contract-driven service compositions using commitments and model checking[J].Expert Systems with Applications,2017(74):151.
- [8] LI Y, WANG Z, FAN J. An extensible consensus algorithm based on PBFT[C]//International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery. Guilin: IEEE,2019:17.
- [9] 涂园超,陈玉玲,李涛,等.基于信誉投票的PBFT改进方案[J].应用科学学报,2021,39(1):79.
- [10] 唐宏,刘双,酒英豪,等.实用拜占庭容错算法的改进研究[J].计算机工程与应用,2022,58(9):144..
- [11] 张逸飞.GCPS连锁故障预警模型及决策支持平台设计研究[D].北京:华北电力大学(北京),2019.
- [12] YUAN X, LUO F, HAIDER M Z, et al. Efficient Byzantine consensus mechanism based on reputation in IoT blockchain[J].Wireless Communications and Mobile Computing,2021(6):8.
- [13] FENG L B, ZHANG H, CHEN Y. Scalable dynamic multi-agent practical Byzantine fault-tolerant consensus in permissioned blockchain[J].Applied Sciences,2018,8(10):1929.
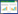 图 1 GPBFT框架
Fig.1 GPBFT framework
图 1 GPBFT框架
Fig.1 GPBFT framework